Квадратичные формы

1. При решении многих задач часто приходится исследовать квадратичные формы.

Определение. Квадратичной формой от переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с определенными коэффициентами:

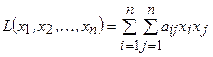(4.10)

Коэффициенты , причем , Матрица

,

составленная из этих коэффициентов называется матрицей квадратичной формы. Так как , то 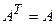, такая матрица называется симметрической.

В матричной записи квадратичная форма имеет вид:

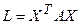, (4.11)

где .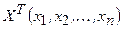

Пример 4.6. Дана квадратичная форма

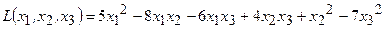. Записать ее в матричном виде.

Решение. Составляем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных 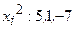. Другие элементы, в силу , равны половинам соответствующих коэффициентов. Поэтому

.

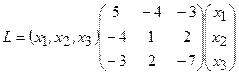2. При невырожденном линейном преобразовании матрица квадратичной формы принимает вид:

, (4.12)

где 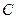- матрица перехода.

Пример 4.7. Найти квадратичную форму 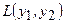, полученную из данной 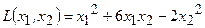при линейном преобразовании , .

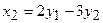Решение. Матрица квадратичной формы 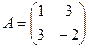, а матрица линейного преобразования 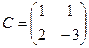. По формуле (4.12) матрица искомой квадратичной формы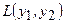

,

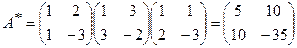следовательно, .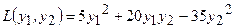

3. Квадратичная форма называется канонической, если все ее коэффициенты , :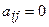

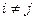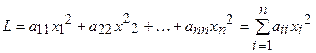, (4.13)

а матрица 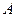является диагональной.

Пример 4.8. Привести к каноническому виду квадратичную форму .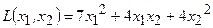

Решение. В начале выделим полный квадрат при 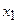, коэффициент при которой отличен от нуля:

.

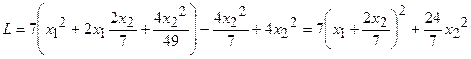Итак, невырожденное линейное преобразование , 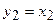приводит данную форму к каноническому виду

Канонический вид квадратичной формы не является однозначно определенным, это можно сделать многими способами.

Например, рассмотренную форму линейным преобразованием 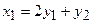, 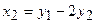можно привести к виду .

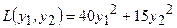Справедлива следующая теорема.

Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.

Ранг квадратичной формы равнее числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях, так же и не изменяется число слагаемых с положительными (отрицательными) коэффициентами (см. Пример 4.8.).

4. Квадратичная форма называется положительно (отрицательно) определенной, если при всех значениях переменных 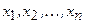, из которых хотя бы одно отлично от нуля, .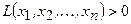

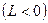Квадратичная форма 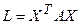положительна тогда и только тогда, если:

а) все собственные числа 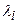матрицы 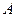положительны;

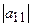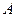б) все главные (угловые) миноры , матрицы положительны (критерий Сильвестра).

Квадратичная форма отрицательно определена, если:

а) все собственные числа 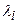матрицы 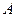отрицательны;

б) все главные (угловые) миноры нечетного порядка отрицательны, а миноры четного порядка – положительны.

Пример 4.9. Доказать, что квадратичная форма 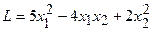является положительно определенной.

Решение. Первый способ. Матрица 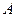имеет вид 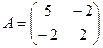. Так как главные миноры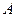 , 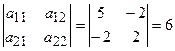положительны, то по критерию Сильвестра квадратичная форма является положительно определенной.

Второй способ. Для матрицы 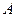характеристическое уравнение имеет положительные корни . Следовательно, на основании критерия квадратичная форма положительно определенная.

Написать квадратичную форму в матричном виде:

4.15. .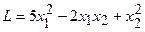

4.16. .

4.17. .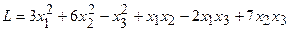

4.18. .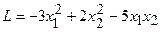

Найти квадратичную форму, соответствующую матрице:

4.19. а) 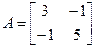, б)

Найти квадратичную форму, полученную из данной линейным преобразованием:

4.20.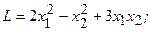

4.21.

Привести к каноническому виду и найти ранг квадратичной формы :

4.22.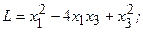

4.23.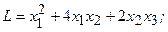

4.24.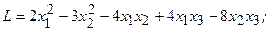

4.25.

Исследовать на знакоопределенность квадратичную форму :

4.26.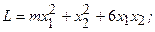

4.27.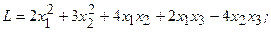

4.28.

4.29.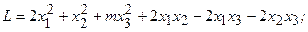

4.30. .

Дата добавления: 2015-05-26