Дифференциальное уравнение теплопроводности Фурье для неподвижной среды

Под дифференциальным уравнением теплопроводности понимают математическую зависимость, обычно выражаемую дифференциальным уравнением в частных производных, характеризующую протекание физического явления переноса тепла и позволяющую рассчитать температурное поле в любой

Выделим в неподвижной однородной и изотропной среде элементарный параллелепипед, объем которого равен 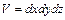. Обозначим q_x [Вт/м²] – тепловой поток, втекающий в левую грань, а 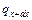– тепловой поток, вытекающий из правой грани. Количество тепла, втекающего в левую грань площадью dydz в единицу времени, равно q_x dydz, а количество тепла, вытекающего через правую грань, равно q_{x + dx} dydz.

Если 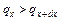, то элементарный параллелепипед будет нагреваться; если – охлаждаться. В итоге, в единицу времени в объеме 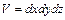будет накапливаться следующее количество тепла . При 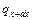стоит знак "–", так как тепло вытекает из объема dxdydz.

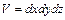В среде может действовать внутренний источник энергии W [Вт/м³]. Тогда в элементарном объеме параллелепипеда будет выделяться в единицу времени количество теплоты . Всего в объеме будет накапливаться суммарное количество тепла в единицу времени .

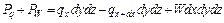По закону сохранения энергии количество тепла, накапливающееся в объеме 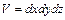в единицу времени, должно быть равно количеству тепла, аккумулируемому средой в единицу времени:

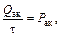Р _ак = Р_q + P_w,

Разложим 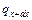в ряд Тейлора: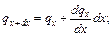

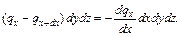
Подставим (1.12) в (1.11) и получим:

Поделим на 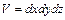и получим дифференциальное уравнение теплопроводности в неокончательном виде:

Согласно закону теплопроводности Фурье: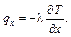

Подставим, получаем: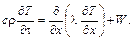

Учитывая, что температура 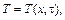и функция внутренних источников тепла 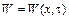являются функциями координаты x и времени t, уравнение теплопроводности для неподвижных сред примет вид

Если можно принять, что 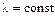, то уравнение можно упростить: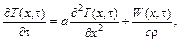

где – коэффициент температуропроводности.

Отметим, что в случае трехмерного температурного поля, уравнение записывают в виде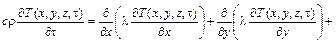

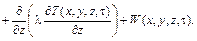
Уравнение записано для плоских тел в декартовой системе. Часто требуется запись уравнений для цилиндрической или сферической систем координат. В этом случае пользуются понятием коэффициента формы г:

- для плоской (декартовой) системы координат г = 0;

- для цилиндрической системы координат г = 1;

- для сферической системы координат г = 2.

С использованием коэффициента формы г уравнения записываются в виде:

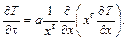
Уравнения описывают перенос тепла во внутренних точках неподвижных сред

Для того, чтобы воспользоваться любым из этих уравнений, их надо дополнить краевыми условиями, включающими в себя:

1) задание геометрии рассматриваемого тела;

2) задание начального условия, определяющего распределение температуры в теле в начальный момент времени;

3) задание граничных условий первого, второго, третьего или четвертого рода, определяющих закономерности теплообмена на граничных поверхностях рассматриваемого образца (тела).

Дата добавления: 2015-05-26