Понятие подпространства

Пусть L – некоторое подмножество векторов линейного пространства V над числовым полем Р.

Определение: Назовем L подпространством пространства V, если подмножество L образует линейное пространство над полем Р относительно операций сложения и умножения на скаляр, определённых в пространстве V.

Само линейное пространство V мы будем рассматривать как подпространство и называть его несобственным, а остальные подпространства в V, не совпадающиес V – собственными. Подмножество L, состоящее из одного нулевого вектора 0, образует, очевидно, подпространство. Это так называемое нулевое подпространство.

Полезен следующий критерий: подмножество L векторов пространства V тогда и только тогда образует подпространство, когда для всякой пары векторов а, b из L и числа 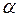из поля Р сумма принадлежит L и произведение 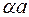также принадлежит L.

Доказательство. 1) Пусть L — подпространство пространства V. Тогда согласно определению пространства в L должны быть выполнимы операции сложения векторов и умножения вектора на число, т. е. сумма векторов а, b из L и произведение 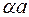вектора а из L на число 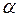из Р должны также принадлежать L.

2) Обратно, пусть в подмножестве L выполнимы операции сложения векторов и умножения вектора на число. Так как L есть часть пространства V, то для векторов из L и подавно будут выполняться аксиомы 2, 3 и 4 определения линейного пространства, а сложение векторов из L будет подчиняться коммутативному и ассоциативному законам. Остается, таким образом, убедиться в существовании нулевого и противоположного вектора. Для этой цели возьмем произвольный вектор а из L. Тогда 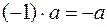в силу выполнимости в L операции умножения вектора на число должно принадлежать L. Далее, в силу выполнимости в L операции сложения векторов должно принадлежать L и . Следовательно, L есть подпространство пространства V ■.

Приведем несколько примеров подпространств.

Пример 1. В пространстве F вещественных функций вещественной переменной х,непрерывных на отрезке [ а, b ], возьмем подмножество L, состоящее из всех многочленов от х. Покажем, что это подмножество есть подпространство пространства F.

В самом деле, если f(х) и g(x) – векторы из L, т. е. некоторые многочлены от х,то сумма f(х) + g(x) и произведение , где 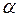– вещественное число, также являются многочленами. Таким образом L есть подпространство пространства F.

Пример 2. Пусть V — трехмерное пространство геометрических векторов с одним и тем же началом О(0, 0, 0). Рассмотрим произвольную плоскость, проходящую через точку О. Нетрудно убедиться, что множество L векторов из V, лежащих на этой плоскости, образует подпространство пространства V.

Пример 3. Пусть V — пространство n -мерных строк над числовым полем Р. Рассмотрим множество L всех тех строк пространства V,которые являются решениями произвольно заданной системы линейных однородных уравнений с п неизвестными с коэффициентами из Р. Это. множество L образует подпространство пространства V, так как сумма решений и произведение решения на число из поля Р являются решениями той же самой системы линейных однородных уравнений.

Обычно такое подпространство L называется подпространством решений данной системы линейных однородных уравнений над полем Р.

Пример 4. Приведем еще один характерный пример подпространства. Пусть V – произвольное линейное пространство над некоторым числовым полем Р. Возьмем какую-нибудь конечную систему векторов 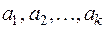пространства V и рассмотрим совокупность L всевозможных линейных комбинаций векторов 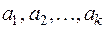, где коэффициенты – 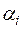числа из поля Р. Легко видеть, что сумма двух таких линейных комбинаций и произведение такой линейной комбинации на число из поля Р являются также линейными комбинациями тех же векторов с коэффициентами из того же поля Р. Следовательно, L есть подпространство пространства. V.

Это подпространство L принято называть линейной оболочкой векторов 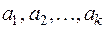или подпространством, натянутым на векторы .

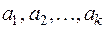Дата добавления: 2015-05-29