Связь базиса и координат вектора в пространстве

Базис

Здесь мы будем изучать основные свойства базиса конечномерного пространства. Прежде всего ответим на вопрос о числе векторов произвольного базиса п- мерного пространства, заданного в предыдущем параграфе.

Теорема 1. Число векторов произвольного базиса п-мерного линейного пространства над числовым полем Р всегда равно размерности п пространства.

Доказательство. Пусть 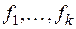— произвольный базис пространства V_n. Возьмем произвольный вектор и поставим ему в соответствие координатную строку 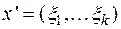(при базисе 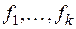). Рассуждая так же, как и при доказательстве теоремы 2 предыдущего параграфа, получаем, что введенное нами соответствие является изоморфным отображением пространства V_k на пространство R_k k -мерных строк над полем Р. С другой стороны, согласно теореме 2, пространство V _n должно быть изоморфно с пространством R_n n -мерных строк над тем же полем Р, Следовательно, пространства R_k и R_n изоморфны.. Но мы знаем, что размерность пространства R_k равна k и размерность пространства R_n равна п, и что два линейных конечномерных пространства над полем Р тогда и только тогда изоморфны, когда размерности их равны (см, теоремы 1 и 3 предыдущего параграфа). Таким образом, k = п, и теорема доказана ■.

Пусть теперь и 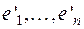– два каких-нибудь базиса линейного пространства V _n над числовым полем Р. Базис 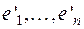(в дальнейшем - новый базис), очевидно, должен линейно выражаться через базис (далее – старый базис):

, (1)

где 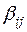– некоторые числа из поля Р. В свою очередь базис должен линейно выражаться через базис .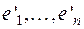

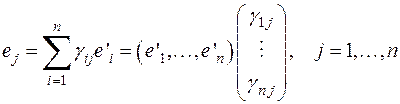, (2)

где 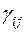– также некоторые числа из поля Р. Систему равенств (1) и систему равенств (2)можно объединить в следующие два равенства:

,

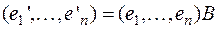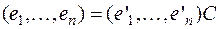, (3)

где B и C квадратные матрицы n -го порядка с элементами из Р:

;

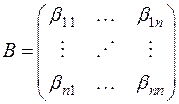Мы видим, что 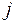-ый столбец матрицы В составлен из координат 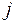-го вектора нового базиса относительно первоначального базиса, 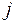-ый столбец матрицы С, составлен из координат 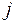-го вектора первоначального базиса относительно нового базиса. Матрица B называется матрицей перехода от базиса к базису 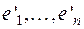, в дальнейшем мы будем обозначать её: . Очевидно, что C есть матрица перехода от базиса 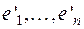к базису , т.е. .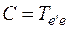

Посмотрим, как связаны между собой матрицы Ви С. Предварительно докажем следующую лемму.

Лемма. Если базис пространства V _a над полем Р и

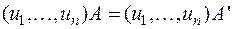(4)

А и A’ — прямоугольные (в частности квадратные) матрицы из п строк и т столбцов с элементами из поля Р, то марицы А и A’ равны.

Доказательство. Пусть

, .

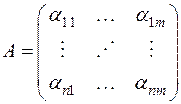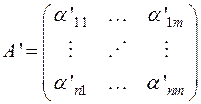Перемножая матрицы 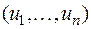и А, а также матрицы 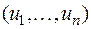и А', получаем из равенства (4) следующее равенство:

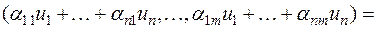
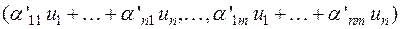
откуда,

, .

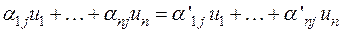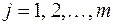Но всякий вектор пространства V_n единственным образом выражается через базис. Следовательно, 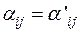, т. е. А = А' ■.

Обратимся теперь к равенствам (3). Подставляя выражение однострочной матрицы из первого равенства (3) во второе равенство (3), получаем: 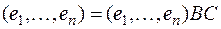или, обозначая через Е единичную матрицу n-го порядка: 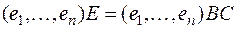откуда в силу только что доказанной леммы 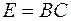, т.е. 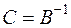или .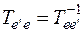

Мы, таким образом, пришли к следующей теореме.

Теорема 2. Матрица перехода B от базиса к базису 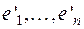пространства V _n - является невырожденной, причем матрица C перехода от базиса 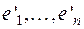к базису является обратной относительно матрицы B.

Утверждение. Всякая квадратная невырожденная матрица 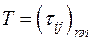порядка п с элементами из поля Р может служить матрицей перехода от одного базиса к другому базису пространства V _n.

Следствие. В п-мерном пространстве V _n существует бесконечное множество базисов, так как можно составить бесконечное множество квадратных невырожденных матриц n-го порядка с элементами из поля Р.

Посмотрим, как изменяются координаты вектора х при переходе от одного базиса к другому.

Обозначим снова через 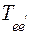матрицу перехода от базиса к базису 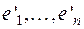пространства V _n. Возьмем произвольный вектор х и напишем в матричной форме его выражение через первый и второй базис:

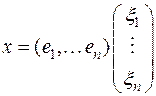, (5)

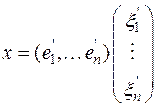. (6)

Подставляя в правую часть равенства (6) вместо 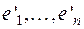произведение , получаем:

.

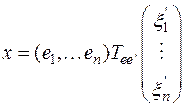Наконец, сравниваем последнее равенство с равенством (5) и находим, что

.

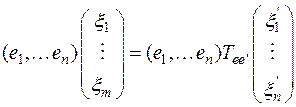Отсюда согласно доказанной выше лемме получается, что

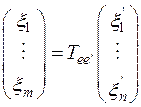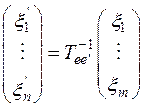, (7)

Пример. Дана матрица перехода :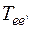

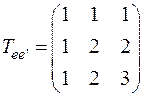
и дан вектор или будем записывать координатный столбец вектора x в базисе : 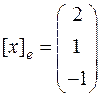. Найти его координаты в новом базисе.

Решение. Применяем вторую формулу (7):

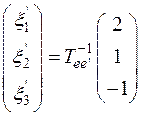
Найдём обратную матрицу:

=>

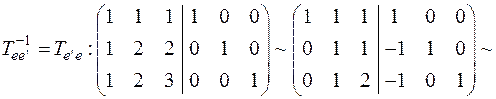
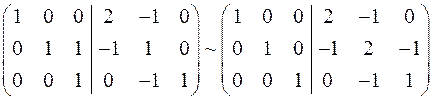
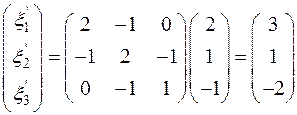или .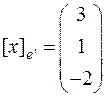

Дата добавления: 2015-05-29