Линейное многообразие (гиперплоскость)

Определение: Назовем подмножество векторов пространства 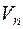линейным многообразием (или гиперплоскостью), полученным путем сдвига подпространства L на вектор х₀, если М есть совокупность векторов вида 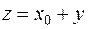, где у — произвольный вектор подпространства L .

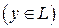Отметим, что фиксированный вектор 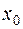, вообще говоря, не принадлежит L и линейное многообразие М может и не быть подпространством.

Пример. В пространстве 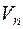над числовым полем Р рассмотрим подмножество М векторов, координатные столбцы которых (при данном базисе) образуют всевозможные решения совместной (в общем случае неоднородной) системы линейных уравнений:

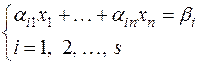. (1)

Обозначим через L подпространство, заданное однородной системой линейных уравнений с теми же коэффициентами:

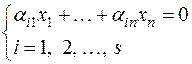. (2)

Мы знаем, что если 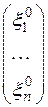– некоторое решение системы (1), то суммы вида 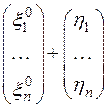, где 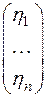любое решение однородной системы (2), исчерпывают все решения системы (1). Отсюда получается, что подмножество М есть совокупность всевозможных сумм вида 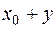, где 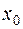вектор с координатным столбцом , а у – произвольный вектор из L. Иными словами, М есть линейное многообразие, полученное путем сдвига подпространства L на вектор .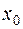

Такое подмножество М мы будем в дальнейшем называть линейным многообразием, заданным системой линейных уравнений (1).

Условимся линейному многообразию приписывать размерность, равную размерности того подпространства, сдвигом которого оно было получено.

Теорема: Данное линейное многообразие – есть результатсдвига только одного подпространства.

Доказательство. Пусть данное линейное многообразие М получается не только путем сдвига подпространства L на вектор 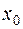, но и путем сдвига другого подпространства 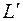на вектор 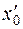. Тогда для любого вектора z из М будет иметь место равенство:

, .

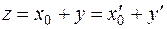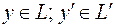Отсюда 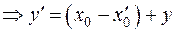, т. е. подпространство 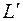есть результат сдвига подпространства L на вектор 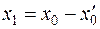. Но в подпространство 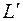должен также входить и нулевой вектор 0. Следовательно, 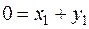, где 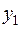— соответствующий вектор из L. 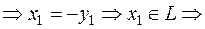. Таким образом, любой вектор 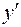подпространства 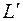есть сумма 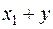двух векторов из L, т. е. вектор из L. Мы видим, что 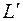есть часть L: 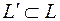. Аналогично из равенства ■.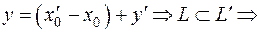

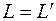Возникает естественный вопрос, исчерпываются ли все линей­ные многообразия линейными многообразиями, заданными системами линейных уравнений.

Теорема: Всякое линейное многообразие М линейного пространства 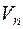может быть задано совместной (в общем случае неоднородной) системой линейных уравнений от n неизвестных, причем ранг этой системы линейных уравнений равен 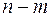, где m – размерность М.

Доказательство. Пусть М — линейное многообразие размерности m, полученное сдвигом подпространства L на вектор 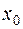. Мы уже знаем, что подпространство L размерности m может быть задано однородной системой линейных уравнений

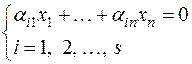(3)

ранга 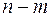. Возьмем из М произвольный вектор z. Он должен иметь вид 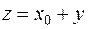, где у — вектор из L. Обозначим координатные столбцы векторов 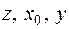соответственно через

.

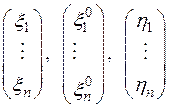Тогда

,

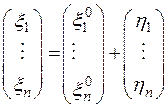откуда 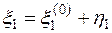, …, 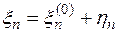. Т.к. координатный столбец вектора y является решением системы (3), то

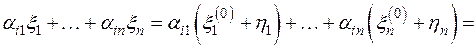
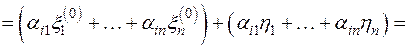
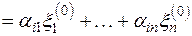
Таким образом, координатный столбец вектора z является решением системы линейных уравнений ранга :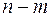

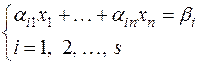(4)

где .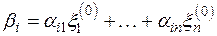

Обратно, пусть 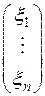– произвольное решение системы (4). Тогда это решение можно представить в виде суммы решения 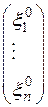системы (4) и некоторого решения 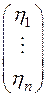однородной системы (3):

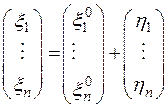. (5)

Обозначим через z и у — векторы, координатными столбцами которых являются соответственно 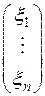и .

Из равенства (5) получается, что 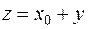, и, очевидно, у должно быть вектором из L. Следовательно, z должно принадлежать М. Мы видим, что линейное многообразие М задается системой линейных уравнений (4) ранга ■.

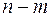Дата добавления: 2015-05-29