F-тест гипотез для нескольких регрессионных коэффициентов

F-тест гипотез для всех регрессионных коэффициентов

Часто проверяется гипотеза о том. что ни один регрессор не оказывает влияния на регрессанд, то есть

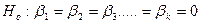(1)

Эта гипотеза для экономических исследований мало интересна.

Вычисление F-статистики вычисляется для (1) 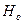по упрощенной формуле

Ее можно записать

где

В этом случае с помощью F-теста проверяется, предоставляют ли m регрессоров как группа влияние на регрессанд.

Тогда значение F-статистики может быть вычислено по формуле

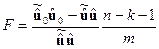
где - сумма квадратов ошибок в регрессии из к регрессорами

- сумма квадратов ошибок в регрессии. из которой исключена группа m исследуемых регрессоров.

Следовательно, в этом случае расчеты делается по двум регрессиям:

1. из к регрессорами (проверяется общая гипотеза)

2. с (k-m) регрессорами (проверяется ограниченная гипотеза).

20. Превращения переменные Нелинейные модели

До сих пор мы рассматривали лишь линейные модели. Одним из недостатков линейного регрессионного анализа есть то, что он может быть применен только к линейным уравнениям.

Например, уравнение вида:

(1)

(2)

является нелинейными. Зависимости (1) и (2) считаются приемлемыми для описания кривых Енгеля, которые характеризуют соотношение между спросом на определенный товар (у) и общей суммой дохода (х).

Много важных связей в эконометрике является нелинейными. Примеры такого рода регрессионных моделей доставляет нам изучение так называемых производственных функций (зависимостей, которые существуют между объемом проведенной продукции и основными факторами производства – трудом и капиталом).

В 1927 г. Пол Дуглас экономист по образованию, обнаружил, что если нанести на одну и ту же диаграмму графику логарифмов показателей реального объема выпуска (У), капитальных расходов (К) и расходов труда (L), то расстояние от точек графика показателей выпуска к точкам графиков показателей труда и капитала будут составлять постоянную пропорцию. Потом он обратился к математику Чарльзу Коббу с просьбой найти математическую зависимость, и Кобб предложил следующую функцию:

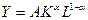(1)

(Они первые, кто использовал для ее построения эмпирические данные).

Нельзя сразу провести линеаризацию путем логарифмирования обеих частей уравнения (1) поскольку мы получим две разных оценки .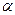

Поэтому разделим обе стороны (1) на L и включим случайный член V.

(2)

Проведем линеаризацию

(3)

Формула Кобба-Дугласа (1), конечно, является частным случаем более общей формулы:

, (4)

где показатели эластичности за расходами капитала и труда не связаны между собой.

Свойства производной функции Кобба-Дугласа.

1. Эластичность выпуска продукции по капиталу и по труды ровная соответственно 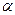и

Следовательно увеличение расходов капитала на 1% приведет к росту выпуска продукции на 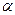%, а увеличение расходов труда на 1% - к росту В на %.

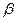Можно допустить, что величина 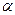и 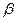находятся между 0 и 1. Они должны быть позитивными.

2. Эффект от масштаба производства

Если и 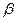в сумме превышают единицу то говорят, что функция имеет растущий эффект от масштаба производства (это значит, что если K и L увеличиваются в некоторой пропорции, то Y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства (Y увеличивается в той же пропорции, что K и L).

3. Прогнозируемые доли производственных факторов.

В соответствии с допущением о конкурентности рынков факторов производства 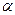и 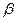имеют последующую интерпретацию как прогнозируемые доли дохода, полученного соответственно за счет капитала и труда.

Если рынок труда имеет конкурентный характер то ставка заработной платы будет равна предельному продукту труда

Следовательно, общая сумма заработной платы будет равна, а частица труда в общем выпуске продукции составит постоянную величину .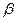

Аналогично, норма прибыли выражается через

И, следовательно, общая прибыль будет равна, а частица прибыли будет постоянной величиной .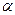

В своей первой работе Кобба-Дуглас подтвердили, что частица труда составила .

Некоторые виды нелинейных зависимостей, которые поддаются непосредственной линеаризации.

I. Зависимости гиперболического типа.

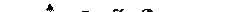1)

Эти функции используются в определенных ситуациях при построении кривых Енгеля спрос-цена, спрос-доход.

Соответствующая кривая регрессии характеризуется двумя асимптотами 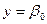- горизонтальная и х=0 - вертикальная. С помощью превращения эта зависимость приводится к линейному виду .

Мы придем к линейной зависимости

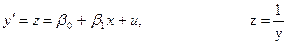
2)

Сделаем замену получим

II Зависимости показательного (экспонентного) типа.

1) Достаточно широкий класс экономических показателей характеризуется приблизительно постоянным темпом относительно прироста во времени. Этому отвечает следующая форма зависимости

Переход к новой переменной дает

2)

Замена

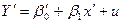
3) Весьма гибкую форму параметризации искомой регрессионной зависимости представляет один из частных случаев так называемой логистической кривой.

Лианеризация:

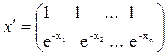
Логические кривые используются для описания показателей, которые имеют определенные «ровные насыщения», например для описания спроса на товар(у) от затраты(х).

III Зависимости степенного типа.

1) Широко распространены в практике социально-экономических исследований степенные зависимости.

Степенная модель множественной регрессии имеет вид

.

При переходе к переменным

Получим линейную модель

Важную роль играют зависимости степенного типа в заданиях построения и анализа производственных функций (Кобба-Дугласа объем – труд, капитал, спрос на товар-доход, цены на данные и другие виды товаров).

Можно показать, что если эластичность в по каждой из объясняющих переменных х постоянная, то в и х могут быть связаны только зависимостью степенного типа.

IV Зависимости логарифмического типа.

Переход к линейному виду

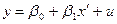
Соответственно

Подбор линеаризующего преобразования.

(Подход Бокса-Кокса).

Мы рассмотрели набор зависимостей, что поддаются линеаризации с помощью соответствующих преобразований анализируемых переменных, но решение вопроса о том, к которому именно из перечисленных линеаризуемых типов зависимостей следует отнести наш конкретный случай, является заданием не простой.

Если ограничиваться парным регрессионным анализом, то можно построить графике наблюдений Y и X как диаграмму рассеяния (разбросу), и это поможет принять решение. Однако часто несколько разных нелинейных функций приблизительно отвечают наблюдением, если они лежат на некоторой кривой. В случае же множественного регрессионного анализа невозможно даже построить график.

Можно, обычно действовать методом «проб и ошибок»: последовательно построить по начальным статистическим данным, которые есть у нас, каждую из линеаризуемых моделей, а затем выбрать из наилучшую в смысле какого-то «критерия качества» (например, по максимальному значению подправленного на несмещенность оценки коэффициента детерминирования(по Тейлу).

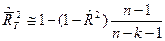
Английские статистики Г. Бокс и Д. Кокс в 1964г. предложили формализированную процедуру подбора линеаризующего преобразования.

Их метод основан на предположении, что искомое преобразование принадлежит определенному однопараметрическому семейству преобразований вида:

Точнее их гипотезу можно сформулировать таким образом:

Существует такое вещественное (позитивное или негативное) число, что из двух нижеследующих вариантов представления искомой регрессионной зависимости между наблюдаемыми переменными Y и X = .

(2)

или (3)

будет удовлетворять всем требованиям нормальной классической линейной модели множественной регрессии.

Замечание 1. Превращения вида (1) применяются обычно к переменным, которые принимают только позитивные значения.

Поэтому если это не так, то сначала подбирают сдвиговые константы которые обеспечивают позитивность значений, а затем к сдвинутым значением переменных применяют данное превращение, то есть

Замечание 2. Семейство степенных превращений вида (1) и весьма широко и гибко.

При модели (1) и (2) является линейными относительно . При мы имеем степенную зависимость между Х и У вида

При других значениях уравнения (1) и (2) будут связывать между собой какие-то степени начальных переменных.

Оценка неизвестного значения параметра

Таким образом, подбор линеаризующего превращения сводится к оценке параметра в формулах (1) и ().

Эта проблема решается с помощью метода максимальной правдоподобности.

Этот метод возводится в следующем.

Вводится функция, которая называется функция правдоподобности.

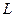- совместимая плотность достоверности появления значений в выборке. (Каждая конкретная выборка может быть представлена определенной точкой в n-мерном пространстве выборок переменных

Если 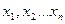независимые и одинаково распределены случайные величины, то функцию правдоподобности можно записать в виде

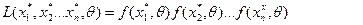(4)

Таким образом, функция, определенная равенством (4), задает достоверность получения, при вытягивании выбором объема n именно наблюдений . Чем большее значение L, тем правдоподобнее или более достоверное появление в результате наблюдений чисел . Отсюда и название функции L – функция правдоподобности.

За оценку неизвестного параметра берется такое число, при котором функция правдоподобности, которая рассматривается как функция от, достигает максимума.

Метод нахождения оценки неизвестного параметра, основанный на требовании максимизации функции правдоподобности, называется методом максимальной правдоподобности.

Функции L и lnL, что рассматриваются как функции параметра достигают максимума при одном и том же значении, поскольку lnL - монотонно растущая функция. Поэтому вместо отыскания максимума функции L находят (что удобнее) максимуму функции lnL.

Функция lnL называется логарифмической функцией правдоподобности.

Следовательно, перейдем к оценке параметра с помощью изложенного выше метода максимальной правдоподобности.

Для определения будем выходить из справедливости представления (3), то есть

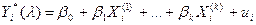
В матричной записи при неизвестном значении параметра связанные между собой уравнением

(5)

X – матрица размерности n x k+1, рангу k+1 .

Для составления уравнений метода максимальной правдоподобности относительно неизвестных параметров 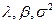при заданных значениях Y и X запишем сначала функцию правдоподобности для преобразованных значений

(6)

а затем, воспользовавшись правилом вычисления закона распределения достоверности сложных величин, которые являются заданными функциями от известных случайных величин, определим нужную нам функцию правдоподобности:

)

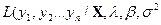для непосредственно наблюдаемых значений .

С учетом взаимной независимости и нормальной распределенности величин имеем

(7)

Тогда, в старых переменных

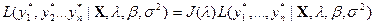
где (8)

J(

где

- якобиан, определитель превращения или в терминах логарифмической функции правдоподобности

(9)

где >0

.

Допустимо, что зафиксировано тогда

или

Следовательно 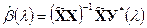(10)

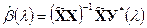
(11)

Для того, чтобы определить оптимальное значение, подставим в (9) оптимальные выражения (10) и (11). И обозначим приобретенного при этом значения l с помощью символа .

(12)

.

Дальше анализируется функция и описывается такое значение, при котором = .

С этой целью определяется априорный диапазон возможных значений (обычно достаточно рассмотреть как область возможных значений отрезок, на этом диапазоне выбирается сетка («решето») значений

.

То значение, при котором

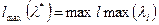
и будет определять искомое линеаризующее преобразование (1). Оценка, и является оценками метода максимальной правдоподобности, а процедуру их поиска часто называют «решетками».

Замечание. Оценка параметра в случае, если превращения (1) применяются одновременно к результирующей и к объясняющим переменным, проводится тем их способом только матрицу Х следует заменить на матрицу наблюдаемых значений преобразованный переменных.

Пример.

Изложен выше подход к підбору линеаризующиего превращения был применен в приложении к анализу функции спроса на деньги.

Результаты предыдущего анализа показали, что функция спроса на деньги, может быть записана в виде

,

где индекс и значит, что значение переменной относится к і-году.

- денежная наличность, включая текущие и срочные депозиты (дефлятированные индексом цен).

- измерен доход (дефлятированные индексом цен).

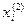- средняя норма процента по коммерческим бумагам (начальные статистические данные – пригодные наблюдения по экономике США из 1869-1963г. n=95 лет).

При реализации «решетчатой» процедуры был определен диапазон возможных значений от к 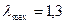и шаг, ровный

Потом для каждого значения были подсчитаны:

где

а также значение и величина

Стандартный регрессионный анализ дат

Можно показать, что функция регрессии спроса на деньги (y) по доходу х^(-1) и средней норме процента х(2) в начальных переменных будем иметь ввиду:

Заносы, что близости оптимального значения говорит о том, что и «логарифмический» вариант функции спроса на деньги (то есть переход к переменным ) находится в приближенным согласи с выборочными данными.

Можно было бы рассчитать и конкурирующую функцию регрессии вида:

Дата добавления: 2015-05-26