Персептрон. Модель МакКаллока-Питтса стала отправной точкой для пост­роения простейшей однонаправленной нейронной сети

д)

Модель МакКаллока-Питтса стала отправной точкой для пост­роения простейшей однонаправленной нейронной сети, названной персептроном. Такую сеть предложил и исследовал Розенблатт [18] в конце пятидесятых - начале шестидесятых годов XX века. На рис. 2.4 представлена структура персептрона, иногда называемого

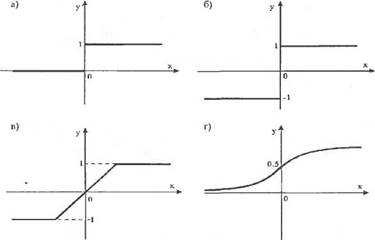
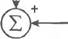
Рис. 2.2. Модель нейрона.

Рис. 2.3. Примеры функции f.

22 Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.3. Персептрон

x(n)r-Mi—I У(п)

d(n)

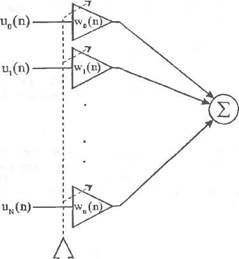Е(П)

Алгоритм обучения персептрона

w(n+1) = w(n) + Ti[d(n) - y(n)] u(n)

Рис. 2.4. Персептрон.

простейшим персептроном. В качестве функции fe модели МакКал-лока-Питтса (2.2) применялась биполярная функция активации (2.4). Сигнал х на выходе линейной части персептрона задается вы­ражением

N

N

х=

(2.8)

i=0

где w₀ = v,u₀ = -1.

Задача персептрона заключается в классификации вектора и =
[и,...... u_N]^T в смысле отнесения его к одному из двух классов, обознача­
емых символами L₁ и L₂. Персептрон относит вектор и к классу L_v если
выходной сигнал у принимает значение 1, и к классу L₂, если выходной
сигнал у принимает значение - 1. После этого персептрон разделяет
/V-мерное пространство входных векторов и на два полупространства,
разделяемые (ЛМ)-мерной гиперплоскостью, задаваемой уравнением

Гиперплоскость (2.9) называется решающей границей (decision boundary). Если N = 2, то решающая граница - это прямая линия, задава­емая уравнением

+ w₂u₂ - v = 0. (2.10)

Точка (и^иг), лежащая над этой прямой (рис. 2.5), относится к клас­су Ц, тогда как точка (и^,и₂), лежащая под этой прямой, относится к клас­су L₂. Точки, лежащие на границе решения, можно произвольно отнести и к классу Ц и к классу L₂.

Для дальнейших рассуждений допустим, что веса ил, / = 0, 1.... N

в уравнении гиперплоскости (2.9) неизвестны, тогда как на вход персеп­
трона последовательно подаются так называемые обучающие сигналы
и(п), п=\,2..... где и(п) = Щп).......... иЛп)]^Т.

Неизвестные значения весов будут определяться в процессе обу­чения персептрона. Такой подход получил название «обучение с учите­лем» или «обучение под надзором». Роль «учителя» заключается в кор­ректном отнесении сигналов и(п) к классам L₁ или /_₂, несмотря на неиз­вестность весов уравнения решающей границы (2.9). По завершении процесса обучения персептрон должен корректно классифицировать по­ступающие на его вход сигналы, в том числе и те, которые отсутствовали

в обучающей последовательности u(n), n = 1, 2...... Кроме того, примем,

что множества векторов u(n), n = 1,2,..., для которых выходной персеп­трона принимает соответственно значения 1 и -1, линейно отделены, т.е. лежат в двух различных полупространствах, разделенных гиперплоскос­тью (2.9). Другими словами, допускается разделение обучающей пос­ледовательности {и(л)} на две последовательности {и^п)} и {и₂(п)} так, что {и,(п)} е Ц и {u₂(n)} e L₂.

В л-й момент времени сигнал на выходе линейной части персеп­трона определяется выражением

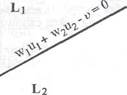
/=с

(2.9)

Рис. 2.5. Решающая граница для N = 2.

Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.4. Системы типа Адалайн

(2.11)

=w^T(n)u(n),

/=о

где

и(п) = [-1, 0,(17), и₂(п)........... и»]⁷, (2.12)

w(n) = [v(n), Wi(n), w₂(n)...... w^n)]^T. (2.13)

Обучение персептрона заключается в рекуррентной коррекции вектора весов w(n) согласно формулам

Г w(n), если w^T(n)u(n)>0 и и(п)е Ц,

win + Л = ■{ т с? 141

^{v ;} I w(n), если w^T(n)u(n)<0 и u(n)e L₂, ⁽ >

Г w(n)-riu(n), если w^T(n)u(n)>0 и u(n)e L₂, ^v ' I w(n)+77u(n), если iv^r(n)(n)<0 и и(п)е Ц, * ^;

где параметр 77 при 0 < т] < 1 - шаг коррекции, тогда как начальные зна­чения компонент вектора весов устанавливаются равными нулю, т.е.

w(0) = 0. (2.16)

Зависимости (2.14) и (2.15) можно представить в более сжатом ви­де. Для этого определим так называемый эталонный (заданный) сигнал d(n) в форме

Г +1, если и(п)е L,,
-{ если u(n)eL₂. (²¹⁷)

Кроме того, отметим, что выходной сигнал персептрона может быть опи­сан выражением

у(п) = sgn(w^r(n)u(n)). (2.18)

С учетом введенных обозначений рекурсии (2.14) и (2.15) прини­мают вид

w(n + 1) = w(n) + [d(n) - у(п)] и(п). (2.19)

Разность d(n) - у(п) можно интерпретировать как погрешность между эталонным (заданным) сигналом d(n) и фактическим выходным сигналом у(п).

Сходимость алгоритма (2.19) исследовал Розенблатт в оригиналь­ной работе [18], а также другие авторы в более поздних публикациях (на­пример, [5, 7, 8]). С учетом принятого выше условия линейной сепара­бельности входных сигналов алгоритм (2.19) сходится, т.е.

w(n_Q) = iv(n₀ + 1) = w(n_Q + 2)=... (2.20)

По завершении обучения решающая граница персептрона опреде­ляется выражением

=0,

(2.21)

;=о

а персептрон корректно классифицирует как сигналы, которые принадле­жат к обучающей выборке {и(п)}, так и не входящие в это множество, но выполняющие условие линейной сепарабельности. Напомним, что усло­вию линейной сепарабельности не отвечает логическая функция XOR, заданная таблицей 2.1.

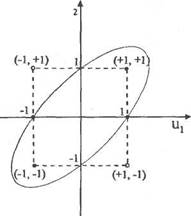
Из рис. 2.6 следует, что не существует прямой, которая отделила бы точки со значениями функции XOR, равными - 1, от точек со значени­ями, равными 1. В этом случае роль примерной границы играет эллипс, и поэтому алгоритм (2.18) не был бы сходящимся. Проблему XOR можно разрешить с помощью двухслойного персептрона. Эта. проблема деталь­но исследована в работах [13] и [24].

2.4. Системы типа Адалайн

Системы типа Адалайн (Adaptive Linear Neuron - адаптивный ли­нейный нейрон) были предложены в 1960 г. Видроу и Хоффом [25]. Вид-роу и Лер [26] описали целое семейство систем типа Адалайн. В настоя-

U

Рис. 2.6. Иллюстрация проблемы XOR.

Таблица 2.1. Логическая функция XOR

"1	и2	d = XOR(u1lt/2)
+1	+1	-1
+1	-1	+1
-1	+1	+1
-1	-1	_-|

Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.4. Системы типа Адалайн

щей главе перед детальным обсуждением систем типа Адалайн (пп. 2.4.2 и 2.4.3) рассмотрим модель так называемого линейного взвешенного сум-матора.

Дата добавления: 2015-06-04