Строится простая (парная) регрессия в случае, когда среди факторов, влияющих на результативный показатель, есть явно доминирующий фактор. 2 страница

Такая точка находится путем приравнивания нулю частных производных функции 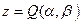по переменным и , т. е. приравниванием нулю производной функции как функции только от при фиксированном ,

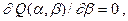(8.17)

и производной функции как функции только от при фиксированном ,

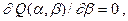
Это приводит к так называемой системе нормальных уравнений

решением которой и является пара , 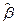. Остается заметить, что согласно правилам вычисления производных,

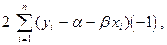(8.18)

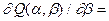
(8.19)

так что искомые значения , 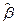удовлетворяют соотношениям

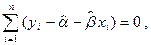
(8.20)

9. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

В теории изучения эконометрики как предполагается, что имеется точная информация о рассматриваемой случайной переменной, в частности — об ее распределении вероятностей (в случае дискретной переменной) или о функции плотности распре деления (в случае непрерывной переменной). С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики, в которых мы можем быть заинтересованы.

Однако на практике, за исключением искусственно простых случайных величин (таких, как число выпавших очков при бросании игральной кости), мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.

Процедура оценивания всегда одинакова. Берется выборка из n наблюдений и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Нужно следить за терминами, делая важное различие между способом или формулой оценивания и рассчитанным по ней для данной выборки числом, являющимся значением оценки. Способ оценивания — это общее правило, или формула, в то время как значение оценки — это конкретное число, которое меняется от выборки к выборке

В табл. 5 приведены формулы оценивания для двух важнейших характеристик генеральной совокупности. Выборочное среднее обычно дает оценку для математического ожидания, а формула 2 в табл. 5 — оценку дисперсии генеральной совокупности.

Таблица 5

Характеристики генеральной совокупности	Формулы оценивания
Среднее, μ
Дисперсия, σ^2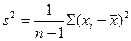

Отметим, что это обычные формулы оценки математического ожидания и дисперсии гене р альной совокупности, однако не единственные. Возможно, вы настолько привыкли использовать х в качестве оценки для μ, что даже не задумывались об альтернативах. Конечно, не все формулы оценки, кото р ые можно представить, одинаково хороши. Причина, по которой в действительности используется х, в том, что эта оценка в наилучшей степени соответствует двум очень важным критериям — не смещенности и эффективности. Эти критерии будут рассмотрены ниже.

Оценки как случайные величины

Получаемая оценка представляет частный случай случайной переменной. Причина здесь в том, что сочетание значений х в выборке случайно, поскольку х — случайная переменная и, следовательно, случайной величиной является и функция набора ее значений. Возьмем, например, — оценку математического ожидания:

(9.1)

Мы только что показали, что величина х в i-м наблюдении может быть разложена на две составляющие: постоянную часть ц и чисто случайную составляющую u_i,:

х_i = μ + u_i (9.2)

С ледова т ельно,

х = μ + u (9.3)

где u - выборочное средне е величин u_i,.

0тсюда можно видеть, что х, подобно х, имеет как фиксированную, так и чисто случайную составляющие. Ее фиксированная составляющая - μ, то есть математическое ожидание х, а ее случайная составляющая - u, то есть среднее значение ч и сто случайной составляющей в выборке.

Величина х считается нормально распределенной. Можно видеть, что распределения, как х, так и х, симмет р ичны относительно μ - т е оретического среднего. Разница между ними в том, что распределение х уже и выше. Величина х, вероятно, должна быть ближе к μ, чем значение единичного наблюдения х, поскольку ее случайная составляющая u есть среднее от чисто случайных составляющих u₁, u₂,… u_n, и в выборке, которые, по-видимому, «гасят» друг друга при расчете среднего. Далее, теоретическая дисперсия величины и составляет лишь часть теоретической дисперсии u.

10. Пример оценки коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

Пример. Доходы семы. Пусть Inc обозначает реальный доход семьи, Expend - ее реальные расходы. Для того чтобы исследовать зависимость расходов от доходов, оценим коэффициенты регрессии Expend на Inc и константу.

Для всех типов семей (количество наблюдений 3594)

Expend = 4663.3 + 0.686 Inc R² = 0.21, s = 11307. (10.1)

(233.6) (0.0223)

В скобках приведены стандартные ошибки коэффициентов регрессии. Соответствующие t- статистики равны 19.96 и 30.81, т. е. коэффициенты статистически достоверно отличаются от нуля. Однако значение коэффициента детерминации R² невелико. Это объясняется, конечно, разнородностью семей как по составу, так и по другим факторам, таким, как место проживания, структура расходов, состав семьи и т. п. Таким образом, для более однородной выборки семей мы вправе ожидать увеличения значения коэффициента детерминации.

Lля семей, состоящих из одного человека (количество наблюдений 509):

Ехреnd = 3229.2 + 0.355 Inc, R² = 0.39, s = 4567. (10.2)

(182.0) (0.0162)

Как и раньше, коэффициенты являются значимыми — t-статистики равны соответственно 17.74 и 20.70. Как мы и ожидали, качество подгонки улучшилось —коэффициент R² возрос с 0.21 до 0.39, а оценка стандартного отклонения остатков s уменьшилась с 11307 до 4567. Так как в семьях из одного человека нет расходов на содержание неработающих членов семьи (дети, престарелые), то на потребление тратится меньшая часть прироста дохода. Склонность к потреблению, определяемая как д Ехреnd/ д Inc, для семьи из одного человека равна 0.355, в то время как в среднем по всей выборке 0.686.

Обозначим через Nf количество членов в семье. Оценим ре грессию среднего расхода на члена семьи на средний доход члена семьи (количество наблюдений 3594):

Ехреnd/ Nf = 2387.2 + 0.447 Inc/ Nf, R² = 0.24, s = 4202. (10.3)

(76.8) (0.0133)

Значение R² увеличилось по сравнению с первой регрессией. Пере ход к удельным данным приводит к уменьшению дисперсии ошибок модели.

11. Оценка дисперсии случайной ошибки модели регрессии

В регрессионном уравнении всегда имеется сопутствующий параметр –дисперсия случайной ошибки σ².

Обозначим через прогноз значения Y_t в точке Х_t. Остатки регрессии е_t определяются из уравнения (11.1)

Остатки е_t, так же как и ошибки ε_t, являются случайными величинами, но остатки наблюдаемы, а ошибки –нет.

В реальных исследованиях дисперсия ошибок σ² неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии а,b. При этом вместо дисперсий оценок получаем оценки дисперсий. При этом вместо σ² используется s².

11.2)

это несмещенная оценка дисперсии ошибок σ².

Также используется следующая формула для определения оценки дисперсии случайной ошибки.

- дисперсия ошибки при конкретном i-м значении фактора,

k_i- коэффициент пропорциональности, меняющийся с изменением величины фактора.

12. Состоятельность и несмещенность МНК-оценок

МНК позволяет получить такие оценки параметров а и b, которых сумма квадратов отклонений фактических значений ре­зультативного признака (у) от расчетных (теоретических) ми­нимальна:

(12.1)

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минималь­ной. (12.2)

Решается система нормальных уравнений

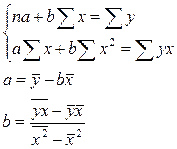(12.3)

Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяет­ся, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в парабо­ле второй степени y=a₀+a₁x+a₂x²+ε заменяя переменные x=x₁,x²=x₂, получим двухфакторное урав­нение линейной регрессии: у=а₀+а₁х₁+а₂х₂+ ε

Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется харак­тер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное), значение результативного признака: приравнива­ем к нулю первую производную параболы второй степени: 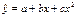, т.е. b+2cx=0 и x=-b/2c (12.4)

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:

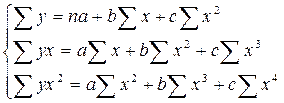(12.5)

Решение ее возможно методом определителей:

(12.6)

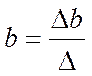(12.7)

(12.8)

При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей , которая представляет собой ненаблюдаемую величину.

Исследования остатков - предполагают проверку наличия сле­дующих пяти предпосылок МНК:

1.случайный характер остатков;

2.нулевая средняя величина остатков, не зависящая от х_i;

3.гомоскедастичность—дисперсия каждого отклонения 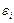,одинакова для всех значений х;

4.отсутствие автокорреляции остатков. Значения остатков , распределены независимо друг от друга;

5.остатки подчиняются нормальному распределению.

Рассмотрим предпосылки МНК

1) Проверяется случайный характер остатков , с этой целью строится график зависимости остатков от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки , представляют собой случайные величины и МНК оправдан, те­оретические значения у_х хорошо аппроксимируют фактические значения y. В других случаях необходимо либо применять дру­гую функцию, либо вводить дополнительную информацию и за­ново строить уравнение регрессии до тех пор, пока остатки , не будут случайными величинами.

2) Вторая предпосылка МНК относительно нулевой средней ве­личины остатков означает, что 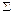(у — у_х) = 0. Это выполнимо для линейных моделей и моделей, нелинейных относительно вклю­чаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков 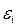от теоретических значений ре­зультативного признака у_х строится график зависимости случай­ных остатков от факторов, включенных в регрессию х_i. Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений x_j. Если же график показывает наличие зависимости и х_j то модель неадек­ватна. Причины неадекватности могут быть разные.

3) В соответствии с третьей предпосылкой МНК требуется, что­бы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора x_j остатки , имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. Гомоскедастичность остатков означает, что дисперсия остат­ков - одинакова для каждого значения х.

4)Отсутствие автокор­реляции остатков, т. е. значения остатков 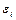распределены неза­висимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечива­ет состоятельность и эффективность оценок коэффициентов ре­грессии.

13. Эффективность оценок МНК. Теорема Гаусса-Маркова

Имея набор наблюдений (Х_t, Y_t), t=1,…n, и модель 1-3ab, зададимся целью оценить все 3 параметра модели: a, b,σ².

Для наилучшей оценки параметров а и b применим теорему Гаусса- Маркова в предположениях модели 1-3ab:

1. Y_t = a + bX _t + ε _t, t = 1,…n;

2. Х_t - детерминированная величина;

3а. Еε _t = 0, Е (ε _t²) = V (ε _t) = σ²

3б. Е(ε _tε_s) =0, при t ≠ s

Оценки , полученные по методу наименьших квадратов (МНК), имеют наименьшую дисперсию в классе всех линейных оценок.

Доказательство.

1. Проверим, что МНК –оценки являются несмещенными оценками истинных значений а,b. Следовательно:

(13.1)

(13.2)

вычислим дисперсии оценок

Представим в виде:

, где (13.3)

Легко проверить, что w_t удовлетворяет следующим условиям:

1) (13.4)

2) (13.5)

3) (13.6)

4) (13.7)

(13.8)

(13.9)

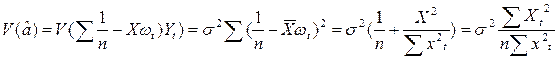(13.10)

Формула (13.10) получается с использованием тождества

в качестве выводов произведем доказательство что МНК - оценка имеет наименьшую дисперсию среди всех несмещенных оценок.

Пусть -любая другая несмещенная оценка. Представим с_t в виде с_t =ω_t + d_t, тогда 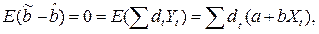(13.11)

для всех а,b. Отсюда

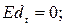
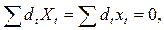(13.12)

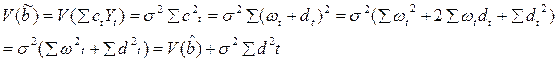Другими словами , а это и есть доказательство теоремы Гаусса –Маркова.

14. Проверка гипотезы о значимости коэффициентов модели парной регрессии с помощью t – статистики Стьюдента.

Оценка статистической значимости параметров регрессии проводится с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н₀ о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t – критерия Стьюдента.

(15.1)

(15.2)

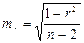(15.3)

(15.4) (15.5) 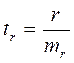(15.6)

Определяется стат. значимость параметров.

t_a ›T_табл - a стат. значим

t_b ›T_табл - b стат. значим

Находятся границы доверительных интервалов.

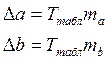(15.7) (15.8) (15.9)

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b находясь в указанных границах не принимают нулевых значений, т.е. не явл.. стат. незначимыми и существенно отличается от 0.

15. Проверка гипотезы о значимости парного коэффициента корреляции

Оценка значимости уравнения регрессии в целом дается с по­мощью F-критерия Фишера. При этом выдвигается нулевая ги­потеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложе­ние общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:

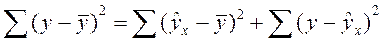(16.1)

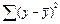- общая сумма квадратов отклонений

- сумма квадратов отклонения объясненная регрессией - остаточная сумма квадратов отклонения.

Любая сумма квадратов отклонений связана с числом степе­ней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых откло­нений из п возможных требуется для образования данной суммы квадратов.

Дисперсия на одну степень свободы D.

(16.2)

F-отношения (F-критерий): (16.3)

Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н₀ необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором раз­работаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F_факт > F_табл Н₀ отклоняется.

Если же величина окажется меньше табличной F_факт ‹, F_табл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Н_о не отклоняется.

Стандартная ошибка коэффициента регрессии

(16.4)

Для оценки существенности коэффициента регрессии его ве­личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое

затем сравнивается с табличным значением при определенном уровне значимости 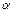и числе степеней свободы (n- 2).

Стандартная ошибка параметра а:

(16.5) (16.6)

Значимость линейного коэффициента корреляции проверя­ется на основе величины ошибки коэффициента корреляции т_r:

(16.7) (16.7)

Общая дисперсия признака х: 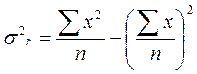(16.8)

Коэф. регрессии (16.9)

Его величина показывает ср. изменение результата с изменением фактора на 1 ед.

Ошибка аппроксимации: 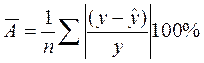(16.10)

16. Проверка гипотезы о значимости уравнения парной регрессии

Пусть выполняется условие, нормальной линейной регрессионной модели ,т.е. ε- многомерная нормально распределенная случайная величина, или что то же самое, Y_t имеют совместное нормальное распределение. тогда МНК –оценки коэффициентов регрессии имеют совместное нормальное распределение, так как они являются линейными функциями от Y_t.:

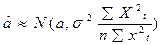, . (17.1)

Если гипотеза значимости уравнений парной регрессии не выполняется, то (17.1) является неверным, однако при условиях стабильности Х_t при росте n оценки a^, b^ имеют асимптотически нормальное распределение, т.е. (17.1) выполняется асимптотически при n → ∞.

Произведем проверку гипотезы о том, что b=b₀

Из (17.1) получаем 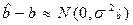, где . Оценка дисперсии оценки получается из формулы . Таким образом,

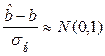, (17.2)

Следовательно

(17.3)

т.е. по определению статистики Стьюдента, имеется

(17.4)

и, так как

, получаем 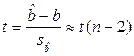(17.5)

Формулу (17.5) применяют для проверки гипотезы Н₀:b = b₀ против альтернативной гипотезы Н₁: b ≠ b₀. Предположим гипотезу Н₀ –верной на 95% уровне. с (n -2) степенями свободы:

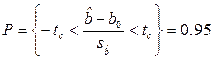(17.6)

Отвергая Н₀, принимаем верной Н₁ на 5% уровне значимости.

17. Пример проверки гипотезы о значимости регрессионных коэффициентов и модели парной регрессии в целом.

Рассмотрим значение коэффициента регрессии.

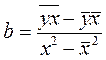(18.1)

Параметр b называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу. Оценку коэффициента регрессии можно получить не обращаясь к методу наименьших квадратов. Альтернативную оценку параметра b можно найти исходя из содержания данного коэффициента: изменение результата сопоставляют с изменением фактора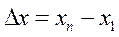

Дата добавления: 2015-06-04