Четырехугольники

С B

Рассмотрим треугольник ∆ АВС. Введем следующие обозначения:

a – длина стороны СВ, b – длина стороны АС, с – длина стороны AB;

p – полупериметр треугольника;

h_a – длина высоты, опущенной на сторону СВ;

h_b – длина высоты, опущенной на сторону AС;

h_c – длина высоты, опущенной на сторону AB.

r – радиус окружности, вписанной в треугольник;

R – радиус окружности, описанной около треугольника;

S – площадь треугольника.

Основные формулы:

S = ½ a h_a

S = ½ a b sinC

S = p r

S = abc/4R

S = (формула Герона)

Теорема косинусов:

c² = a² + b² – 2abcosC

Теорема синусов:

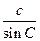= = = 2R

Основные соотношения в прямоугольном треугольнике:

CH – высота

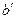Пусть – длина отрезка ВH, – длина отрезка AH. Тогда

1) ,

2) ,

3)

Теорема Пифагора:

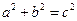
Некоторые теоремы о треугольниках и углах

1. Сумма углов треугольника равна 180º.
2. Каждая сторона треугольника меньше суммы двух других сторон.
3. В равнобедренном треугольнике биссектриса угла при вершине является медианой и высотой.
4. В равнобедренном треугольнике углы при основании равны.
5. Центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
6. Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.
7. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.
8. Первый признак равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
9. Второй признак равенства треугольников: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
10. Третий признак равенства треугольников: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
11. Средняя линия треугольника параллельна стороне и равна ее половине.
12. Две прямые, пересеченные секущей параллельны тогда и только тогда, когда накрест лежащие углы равны.
13. Две прямые, пересеченные секущей параллельны тогда и только тогда, когда соответственные углы равны.
14. Две прямые, пересеченные секущей параллельны тогда и только тогда, когда сумма односторонних углов равна .
15. Медианы треугольника делятся точкой пересечения на отрезки, длины которых относятся как 2:1, считая от вершины треугольника.
16. Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
17. Первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
18. Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
19. Третий признак подобия треугольников: если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
20. В подобных треугольниках сходственные высоты, медианы, биссектрисы, радиусы описанной и вписанной окружностей пропорциональны сходственным сторонам.
21. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
22. Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют .
23. Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют .

Пример 1. В треугольнике ABC угол А равен 37º. Внешний угол при вершине В равен 65º. Найдите угол С.

Решение. Внешним углом треугольника при вершине B называется угол, смежный с углом треугольника при вершине В. Следовательно, угол треугольника при вершине В равен

180º – 65º = 115º. По свойству суммы углов треугольника (теорема 1) угол С равен

180º – 37º – 115º = 28º.

Ответ: 28º.

Пример 2. Длины отрезков равны 1, m и n, где m и n – целые числа. Сколько треугольников можно составить из этих отрезков, если m может принимать значения из отрезка [2;4], а n из отрезка [3; 8]?

Решение. Поскольку для значения m имеется 3 варианта, а для значения n – 6 вариантов, то всего имеется 18 вариантов выбора длин трех отрезков. Перебором этих вариантов можно установить, что в соответствии с теоремой 2 для составления из отрезков треугольника подходит только два варианта: m = n = 3 и m = n = 4.

Ответ: два треугольника.

Пример 3. В равнобедренном треугольнике АВС угол между основанием АС и высотой АD, проведенной к боковой стороне ВС, равен 33º. Найдите угол при вершине В треугольника.

Решение. Вставить рис. 11

В треугольнике АDС угол С равен 180º – 33º– 90º = 57º. Поскольку треугольник АВС равнобедренный, угол А равен углу С (теорема 4). Следовательно, угол В равен

180º – 57º – 57º = 66º.

Ответ: 66º.

Пример 4. В прямоугольном треугольнике АВС проведены биссектрисы острых углов АD и ВЕ, пересекающиеся в точке О. Верно ли, что в случае, когда треугольник равнобедренный, величина угла АОВ меньше, чем других случаях?

Решение. Рассмотрим треугольник АОВ. Обозначим величину угла ОАВ буквой α и величину угла ОВА буквой β. Тогда угол АОВ равен 180º – α – β. Поскольку АD и ВЕ – биссектрисы, угол САВ равен 2α, а угол СВА равен 2β. Значит 2α + 2β = 180º – 90º = 90º. Следовательно, α + β = 45º. Отсюда следует, что угол АОВ равен 180º – 45º = 135º. Таким образом, величина угла АОВ не зависит от соотношения между катетами треугольника.

Ответ: не верно.

Пример 5. Основание АС равнобедренного треугольника АВС равно 80 см, а высота ВH равна 30 см. Найдите высоту АМ, опущенную на боковую сторону треугольника.

Решение. В равнобедренном треугольнике высота является также медианой (теорема 3). Следовательно, АH = 40 см. По теореме Пифагора найдем гипотенузу ВС прямоугольного треугольника ВСН: ВС² = СН² + ВН² = 1600 + 900 =2500, отсюда ВС = 50 см. Вычислим площадь треугольника АВС двумя способами:

S_АВС = ½ AC∙BH

S_АВС = ½ BC∙AM.

Отсюда следует, что

Ответ: 48 см.

Пример 6. В треугольнике АВС угол А равен 21º, а угол С равен 69º. Найдите угол между медианой ВМ и биссектрисой ВD.

Решение. Угол В равен 180º – 21º– 69º = 90º, следовательно, треугольник АВС – прямоугольный. По теореме 7 точка М (середина гипотенузы) является центром описанной окружности. Значит, АМ = ВМ = СМ. Таким образом, треугольник АВМ – равнобедренный, следовательно, угол АВМ равен 21º. Угол АВD равен 45º (поскольку ВD – биссектриса). Искомый угол МВD равен 45º – 21º = 24º.

Ответ: 24º.

Основные формулы

Площадь S любого выпуклого четырехугольника вычисляется по формуле:

S = ½ d₁ d₂ sinα, где d₁, d₂ – диагонали, α – угол между диагоналями.

Для ромба эта формула принимает вид:

S_ромба = ½ d₁ d₂

Площадь S параллелограмма вычисляется по формулам:

S = a h_a, где а – сторона параллелограмма, h_a – высота, опущенная на эту сторону;

S = a b sinα, где а и b – стороны параллелограмма, а α – угол между ними.

Для ромба эта формула принимает вид:

S_ромба = а² sinα.

Площадь S трапеции вычисляется по формуле:

S = ½ (a + b) h, где a и b – основания трапеции, h – высота трапеции.

Некоторые теоремы о четырехугольниках

1. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон четырехугольника равны.
2. Около четырехугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов четырехугольника равны 180º.
3. Сумма всех углов четырехугольника равна 360º.

23. В параллелограмме противоположные стороны равны, противоположные углы равны,

24. Диагонали параллелограмма точкой пересечения делятся пополам.

25. Диагонали прямоугольника равны.

26. Диагонали ромба взаимно перпендикулярны и делят углы ромба пополам.

27. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

Пример 7. Острый угол ромба равен 60º. Площадь ромба равна 2 . Найдите радиус вписанной в ромб окружности.

Решение. Площадь ромба можно вычислить по формуле S = а² sinα. Подставим в эту формулу S = , sinα = sin60º = 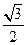.Тогда а² = 4, а =2. С другой стороны, площадь ромба равна a h_a, следовательно, 2 = 2 h_a, откуда h_a = . Высота ромба равна диаметру вписанной окружности, значит, радиус вписанной в ромб окружности равен .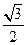

Ответ: .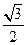

Пример 8. Окружность вписана в трапецию с боковыми сторонами 9 и 17. Найдите среднюю линию трапеции.

Решение. Поскольку в трапецию вписана окружность, по теореме 24 суммы противоположных сторон трапеции равны. Значит, сумма оснований трапеции равна 9 + 17 = 26, откуда следует, что средняя линия трапеции равна 13 (теорема 27).

Ответ: 13.

Пример 9. Четырехугольник ABCD вписан в окружность. Угол ABC равен 100º, угол CAD равен 25º. Найдите угол ABD.

Решение. Угол СAD и угол СBD являются вписанными углами, опирающимися на одну дугу, следовательно, они равны. Значит угол СBD равен 25º. Углы ABD и СBD в сумме составляют угол ABC, значит, их сумма равна 100º. Отсюда следует, что угол ABD равен 100º – 25º = 75º.

Ответ: 75º.

Пример 10. В прямоугольной трапеции ABCD углы А и В – прямые, а величина угла С относится к величине угла D как 1: 3. Найдите острый угол трапеции.

Решение. Очевидно, что острым углом трапеции является угол С. По теореме 26 сумма всех углов трапеции равна 360º. Углы А и В составляют по 90º, следовательно, сумма углов С и D равна 180º. Обозначим величину угла С буквой x, тогда величина угла D равна 3х. Тогда х + 3х = 180º, х = 45º.

Ответ: 45º.

Дата добавления: 2015-06-04