Линейные дифференциальные уравнения

Линейным дифференциальным уравнением порядка n называется уравнение вида

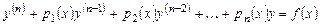. (6.1)

Отличительной чертой линейного уравнения является то, что искомая функция 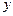и все её производные входят в это уравнение линейно. Предполагается, что заданные функци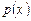и и 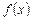непрерывны в некотором промежутке .

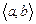Зaдача Коши для этого уравнения при сделанных предположениях имеет единственное решение, если 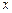принадлежит промежутку .

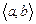Если в уравнении (6.1) правая часть 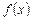тождественно равна нулю, то уравнение называется линейным однородным (ЛОДУ), в противном случае - линейным неоднородным (ЛНДУ). Линейное однородное дифференциальное уравнение имеет вид:

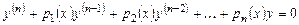. (6.2)

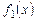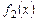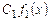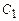Если функции и являются решениями линейного однородного уравнения (6.2), то , где - произвольная постоянная, и сумма 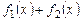также являются решениями этого дифференциального уравнения.

Если функции 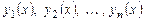являются решениями дифференциального уравнения (6.2), то их линейная комбинация

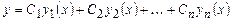, (6.3)

где 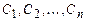- произвольные постоянные, также является решением уравнения (6.2).

Функции 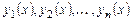называются линейно независимыми в промежутке 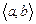, если равенство

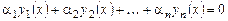, (6.4)

где 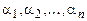- постоянные, имеет место только тогда, когда равны нулю все коэффициенты .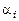

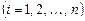Если же равенство (6.4) имеет место на 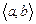при условии, что хотя бы один коэффициент 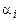отличен от нуля, то система функций 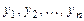- линейно зависимая.

Если 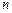функций 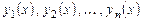являются решениями линейного однородного дифференциального уравнения (6.2) и линейно независимы на промежутке 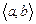, то общее решение уравнения (6.2) имеет вид:

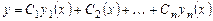, (6.5)

где 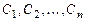- произвольные постоянные.

Система из любых n линейно независимых решений ЛОДУ (6.2) называется фундаментальной системой решений (ФСР) этого уравнения.

Если функции 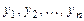определены и 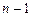раз дифферен-цируемы на промежутке 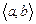, то может быть построен следующий определитель n -го порядка:

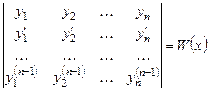.(6.6)

Это - определитель Вронского (или вронскиан) для данной системы функций. С его помощью устанавливается, является ли система решений уравнения линейно независимой. Применение вронскиана основано на следующих теоремаx.

Теорема 1. Если функции 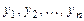линейно зависимы, то вронскиан системы тождественно равен нулю.

Теорема 2. Если функции 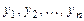- линейно независимые решения, удовлетворяющие некоторому ЛОДУ n -го порядка с непрерывными коэффициентами, то вронскиан такой системы не обращается в нуль ни в одной точке промежутка .

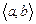Таким образом, чтобы проверить линейную независимость решений 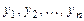ЛОДУ (6.2), надо составить определитель Вронского 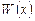и убедиться, что при любом значении 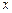из промежутка 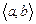он не равен нулю.

Пример 6.1. Показать, что система функций 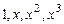линейно независима на всей оси OX. Очевидно, что это есть система решений уравнения 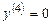на R..

Составим определитель Вронского:

W (x) = = 12 ,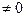

что доказывает линейную независимость функций .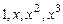

Пример 6.2. Найти определитель Вронского для системы функций 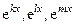, где числа k,l, m различны. Очевидно, это решения такого ЛОДУ:

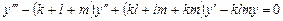на .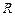

W(x) =

=

.

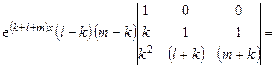
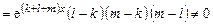Это доказывает линейную независимость функций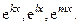

Линейные однородные уравнения с постоянными коэффициентами n - го порядка. Общий вид уравнения:

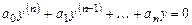, (6.7)

где 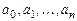- вещественные постоянные, .

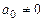Решение уравнения (6.7) ищем в виде экспоненты .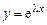

Наводящие соображения: поскольку уравнение представляет собой тождественно равную нулю линейную комбинацию функции y и её производных, следует искать решение в виде функции, не меняющей свой вид при дифференцировании.

Подставив 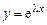в уравнение (6.7), получим

.

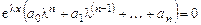Здесь 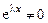, следовательно,

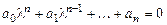. (6.8)

Это - характеристическое уравнение для (6.7); пусть 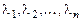- его корни.

Возможны четыре случая.

1. Корни 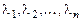- вещественные и различные. Тогда фунда-ментальная система решений уравнения (6.7) имеет вид: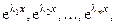

(каждому корню соответствует одна функция в ФСР), а общее решение уравнения (6.7)

2. Корни характеристического уравнения вещественные, среди них есть кратные. Пусть 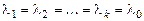, а остальные корни различные. Тогда фундаментальная система решений имеет вид:

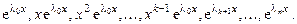
Корню 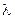кратности k соответствует k функций в ФСР, а общее решение уравнения:

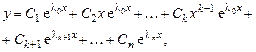
где 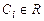, 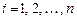- произвольные коэффициенты.

Пример 6.3. .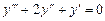

Решение ищем в виде 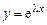. Подставив в уравнение, получим характеристическое уравнение:

,

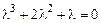или

.

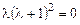Корни 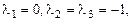- действительные, один из корней двукратный, поэтому общее решение:

.

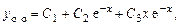
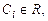
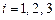3. Среди корней характеристического уравнения eсть комплексные однократные, например 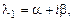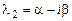, а 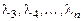- действительные различные. Фундаментальная система решений в этом случае имеет вид:

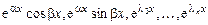
(паре комлексно-сопряженных корней соответствует пара функций в ФСР), а общее решение

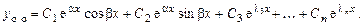
4. Среди корней характеристического уравнения есть комплексно-сопряженные 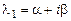и 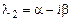кратности k.

В этом случае фундаментальная система решений имеет вид:

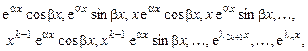
а общее решение:

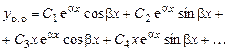
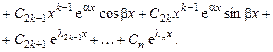
Пример 6.4. .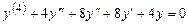

Решение ищем в виде экспоненты 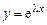. Подставив 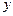в уравнение, получим характеристическое уравнение:

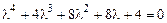или .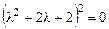

Оно имеет двукратные комплексные корни:

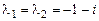и .

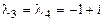Общее решение уравнения имеет вид:

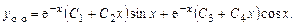
Линейные неоднородные уравнения с постоянными коэффици-ентами n-го порядка. Пусть дано дифференциальное уравнение:

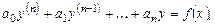
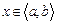(6.9)

с постоянными коэффициентами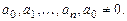

Теорема. Общее решение неоднородного уравнения (6.9) равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения.

Отыскание общего решения соответствующего однородного урав-нения осуществляется по правилам, изложенным в начале шестого раздела. Частное решение неоднородного уравнения для случая правых частей специального вида находится методом подбора, или иначе, методом неопределенных коэффициентов.

Общий вид правой части уравнения (6.9), при котором применим метод неопределенных коэффициентов, следующий:

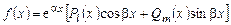. (6.10)

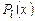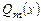Здесь и - многочлены степени l и m соответственно.

В этом случае частное решение уравнения (6.9) ищем в следующем виде:

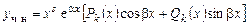, (6.11)

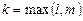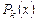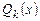где , и - многочлены от 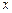степени k обще-го вида с неопределенными коэффициентами, а 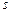- кратность корня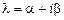 характеристического уравнения. (Если 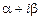не является корнем, то .)

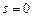Пример 6.5. .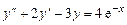

Решение. Сначала найдем общее решение соответствующего одно-родного уравнения

.

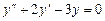Его характеристическое уравнение:

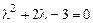или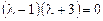

имеет корни 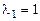и .

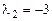Общее решение однородного уравнения:

.

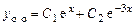Теперь нужно найти частное решение неоднородного уравнения. Сравнивая его правую часть с формулой (6.11), видим, что 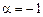, 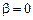. Число 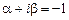корнем характеристического уравнения не является, следовательно, 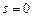. P и Q - многочлены нулевой степени, следова-тельно, частное решение будем искать в виде

.

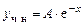Удобно расположить в столбик, написав слева значения коэффициентов из исходного уравнения:

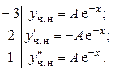
Сложив всё, получим:

,

,

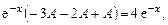
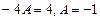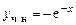а общее решение неоднородного уравнения

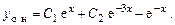
Пример 6.6.

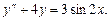
Решение. Однородное уравнение имеет вид

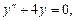
его характеристическое уравнение:

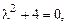корни .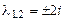

Общее решение

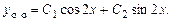
Чтобы правильно выбрать вид частного решения неоднородного уравнения согласно формуле (6.11), сравним правую часть уравнения с общим её представлением по формуле (6.10). Очевидно, 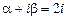является однократным корнем характеристического уравнения, поэтому .

(В физике это явление называется резонансом, суть его в совпадении собственной частоты колеблющейся системы и частоты приложенной внешней силы.)

Кроме того, замечаем, что степени многочленов P и Q - нулевые.

Вид частного решения:

.

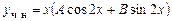Подставим в исходное уравнение:

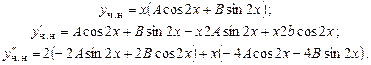
В итоге

;

, .

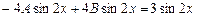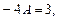
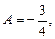
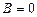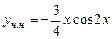Общее решение:

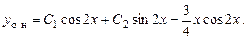
Дата добавления: 2015-06-04