
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные свойства пределов
1.  , где С – постоянная.
, где С – постоянная.
2.  , где С – постоянная.
, где С – постоянная.
3. 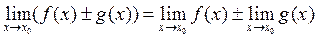 . (1)
. (1)
4. 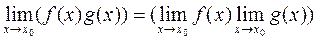 .
.
5. 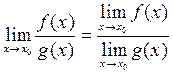 , если
, если 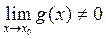 .
.
Сформулированные свойства справедливы не только в том случае, когда переменная х стремится к конечному значению х0, но и при  или
или 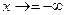 . Как уже отмечалось, при вычислении пределов существенную роль играет понятие непрерывности функции. Напомним, что функция называется непрерывной в точке х0, если справедливо равенство
. Как уже отмечалось, при вычислении пределов существенную роль играет понятие непрерывности функции. Напомним, что функция называется непрерывной в точке х0, если справедливо равенство
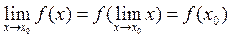 (2)
(2)
т.е. предел функции, непрерывной в предельной точке, равен значению функции в этой точке. Можно доказать, что элементарные функции непрерывны во всех точках, в которых они определены. Как известно к основным элементарным функциям, в частности, относятся: целая рациональная  , где
, где  ; дробно-рациональная
; дробно-рациональная 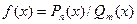 , где
, где 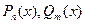 -многочлены произвольных степеней n и m, степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические функции. К элементарным функциям, помимо основных, относятся функции, образованные из основных с помощью арифметических действий.
-многочлены произвольных степеней n и m, степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические функции. К элементарным функциям, помимо основных, относятся функции, образованные из основных с помощью арифметических действий.
Линейная функция у=х-3 является элементарной, определенной, а следовательно и непрерывной при всех действительных значениях х. Тогда  вычисляется по (2) при любых значениях х0. Например,
вычисляется по (2) при любых значениях х0. Например, 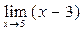 =5-3=2. Аналогично
=5-3=2. Аналогично 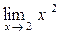 =22=4.
=22=4.
Для вычисления пределов в более сложных случаях, вводится понятие бесконечно малой (б.м.) и бесконечно большой (б.б.) величин.
Функция 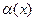 называется б.м. при
называется б.м. при 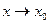 (при
(при 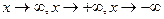 ), если имеет место равенство
), если имеет место равенство 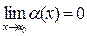 (
(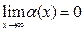 и т.д.). Например, рассмотренная ранее функция у=х -3 является б.м. при
и т.д.). Например, рассмотренная ранее функция у=х -3 является б.м. при 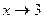 . Действительно,
. Действительно,  . Функция
. Функция  является б.м. при
является б.м. при 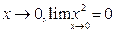 .
.
Функция  называется б.б. при
называется б.б. при 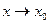 (при
(при 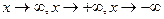 ), если ее значение неограниченно возрастает по абсолютной величине при
), если ее значение неограниченно возрастает по абсолютной величине при 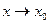 (при
(при  ). В таком случае будем писать
). В таком случае будем писать 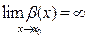 , или
, или 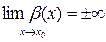 , если
, если  , возрастая по абсолютной величине, принимает только положительные (отрицательные) значения. Например у=2х – б.б. при
, возрастая по абсолютной величине, принимает только положительные (отрицательные) значения. Например у=2х – б.б. при 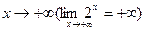 ; y=tg(x) – б.б. при
; y=tg(x) – б.б. при 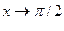 (
(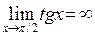 ),
),  -б.б. при
-б.б. при 
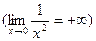 .
.
Справедливы следующие свойства б.м. и б.б. величин Пусть 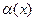 - б.м. и
- б.м. и  - б.б. при
- б.б. при 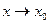 , а функция f(x) – имеет конечный, отличный от нуля предел при
, а функция f(x) – имеет конечный, отличный от нуля предел при 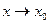 ,
,
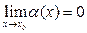 ,
,  ,
, 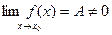 ,
,
тогда
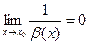 ,
,  ;
; 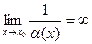 ,
,  б.б.;
б.б.;
 ,
, 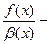 б.м.;
б.м.;  ,
,  б.м (3)
б.м (3)
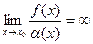 ,
, 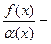 б.б.;
б.б.;  ,
,  б.б.
б.б.
Свойства (3) справедливы и при 
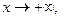
 .
.
Рассмотрим 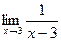 . Функция
. Функция 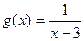 не определена при х =3. Если подставить в выражение
не определена при х =3. Если подставить в выражение 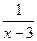 значение х =3, формально получим
значение х =3, формально получим 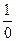 . Чтобы вычислить указанный предел, необходимо учесть свойство (3). Как отмечалось ранее, функция f(x)=x -3 является б.м. при
. Чтобы вычислить указанный предел, необходимо учесть свойство (3). Как отмечалось ранее, функция f(x)=x -3 является б.м. при 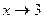 , следовательно,
, следовательно, 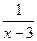 - б.б при
- б.б при 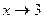 , так что
, так что 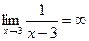 . И так, гипербола
. И так, гипербола 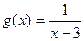 является б.б при
является б.б при 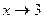 и б.м. при
и б.м. при 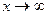 . График функций
. График функций  и
и 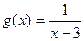 приводится на Рис.5
приводится на Рис.5
Обратимся к понятию неопределенности. Если непосредственная подстановка предельного значения переменной в выражение, стоящее под знаком предела, приводит формально к одному из результатов  , то говорят, что имеет место неопределенность одного из указанных видов. Отметим, что выражение
, то говорят, что имеет место неопределенность одного из указанных видов. Отметим, что выражение  и
и 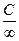 , где С – постоянная, не являются неопределенностями, а приводят, согласно свойствам (3), к б.б, б.м. величинам, соответственно.
, где С – постоянная, не являются неопределенностями, а приводят, согласно свойствам (3), к б.б, б.м. величинам, соответственно.

Рис.5
|
|
Дата добавления: 2015-06-04; Просмотров: 444; Нарушение авторских прав?; Мы поможем в написании вашей работы!