Производная и дифференциал

Начало дифференциального и интегрального исчисления.

Напомним определение основного понятия дифференциального исчисления – производной.

Пусть х₀ фиксированное значение аргумента функции f(x), определенной на промежутке Х. Придадим значению х₀, отличное от нуля приращение ∆ х такое, что х₀ +∆ х тоже принадлежит Х. Отметим, что приращение ∆ х может быть любого знака. Приращению ∆ х соответствует приращение функции ∆ f(х₀)=f(х₀ +∆ х) - f(х₀). Тогда, если существует конечный предел отношения приращения∆ f(х₀) функции f(x) к приращению аргумента ∆ х при стремлении ∆ х к нулю, то он называется производной функции f(x) в точке х₀ и обозначается f′(х₀):

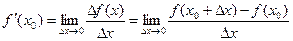. (4)

Полученная по формуле (4) производная f′(х₀) – число. Если предел в (4) равен бесконечности, то говорят, что функция f(x) имеет в точке х₀ бесконечную производную. Возможен также случай, когда предел (4) не существует.

Из курса физики известно, что если за время ∆t = t - t₀ пройдено расстояние ∆S, то средняя скорость за время равна , а предел 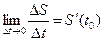является скоростью движения в момент t₀, которую называют мгновенной скоростью .

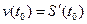Тогда для произвольной функции f(x) отношение 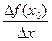- средняя скорость изменения функции f(x) при изменении аргумента на величину ∆ х, а 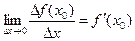- есть мгновенная скорость изменения функции f(x) при значении аргумента х₀.

Например, если функция у=f(x) описывает зависимость полных издержек производства у от объема выпускаемой продукции х, то 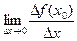- себестоимость продукции при данном объеме производства х₀.

Если предел (4) существует для всех значений х из Х, то каждому х можно сопоставить значение предела 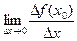и тем самым задать новую функцию, которую называют производной функции f(x) и обозначается 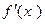. Возможны и другие обозначения производной, например, 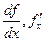. Индекс х в 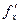указывает переменную, по которой вычисляется производная.

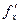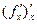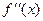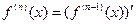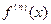Поскольку является функцией, то от нее тоже можно взять производную , которая будет производной второго порядка или второй производной (или ) от исходной функции f(x). Аналогично , где и 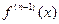- производные n -го (n -1) –го порядка, соответственно.

Обратимся к геометрическому смыслу производной. Выберем на графике функции f(x) (Рис.6) две точк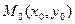и и 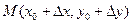, абсциссы которых отличаются на приращение ∆ х, а ординаты, соответственно на 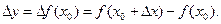Проведем секущую через точки М₀ и М и обозначим 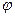, отсчитанный против часовой стрелки угол, который секущая образует с положительным направлением оси абсцисс. При стремлении ∆ х к нулю точка М, перемещаясь по графику функции, стремится к точке М₀, при этом секущая ММ₀, поворачивается вокруг точки М₀ и стремится занять предельное положение касательной, проведенной к графику функции через точку М₀. Обозначим 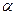угол, который касательная образует с положительным направлением оси абсцисс. Тогда из треугольника ∆ М₀КМ имеем:

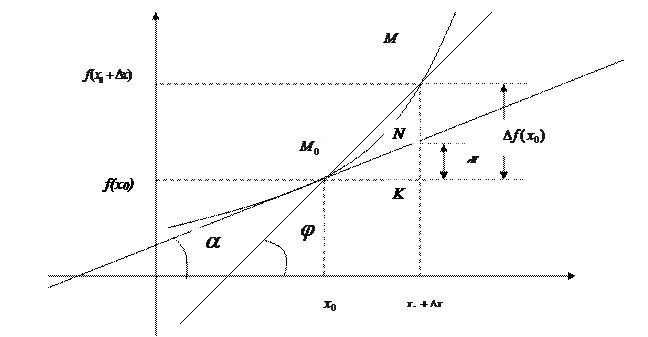
Рис.6

.

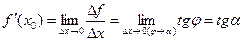Следовательно, если производная функции f(x) в точке х ₀ существует и конечна, то ее значение равно тангенсу угла наклона касательной, проведенной к графику функции в точке .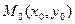

Как видно из рис.6, приращение функции 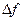, соответствующее приращению аргумента 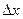, равно приращению ординаты кривой

.

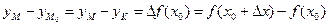Из геометрического смысла производной и свойств треугольника ∆ М₀КМ следует, что приращение ординаты касательной равно

.

Из рис.6 видно, что отрезок МК не равен отрезку NK, т.е. 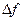не равно 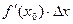. Можно показать, что если в точке х функция f(x) имеет конечную производную, то справедливо равенство

.

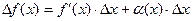где 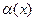- бесконечно малая величина при . Линейная по 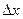часть 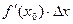приращения 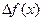называется дифференциалом функции и обозначается df, т.е. 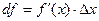. Если 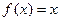то 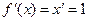(см. ниже табл. производных), так что , т.е. дифференциал независимой переменной совпадает с ее приращением. Тогда для дифференциала df функции f(x) имеем

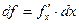. (5)

Именно так обычно и записывается дифференциал первого порядка или просто дифференциал. Помимо дифференциалов первого порядка можно определить дифференциалы высших порядков:

.

Производная любой функции может быть вычислена по определению (4). Однако, вычисления значительно упрощаются, если применять правила дифференцирования и таблицу производных, содержащую производные от элементарных функций. Эти производные можно получить по формуле (4).

Таблица производных

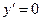
1)		8)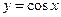
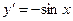
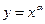
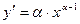
2)		9)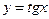
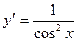
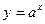
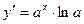
3)		10)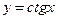
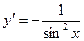
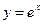
4)		11)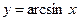
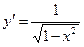
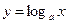
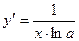
5)		12)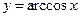
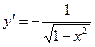
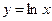
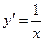
6)		13)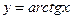
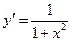
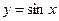
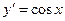
7)		14)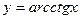

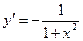
Дата добавления: 2015-06-04