Достаточность

Необходимость

Пусть 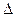есть полный дифференциал, т. е.

.

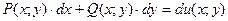Учитывая, что 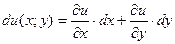(см. р.1.1), имеем:

; .

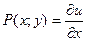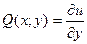Дифференцируя эти равенства по у и по х соответственно, получаем

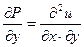и .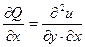

А так как смешанные частные производные 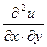и 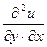равны между собой (см. р.3.1), получаем (4.19).

Пусть в области D выполняется условие (4.19). Покажем, что существует функция и(х; у) в области D такая, что

du(x; у) = Р(х; у)·dx + Q(x; у)·dy.

Найдем эту функцию. Искомая функция должна удовлетворять требованиям:

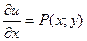и 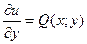. (4.20)

Если в первом уравнении (4.20) зафиксировать у и проинтегрировать его по x, то получим:

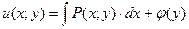. (4.21)

Здесь произвольная постоянная 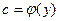зависит от у (либо является числом). В решении (4.21) не известна лишь 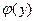. Для ее нахождения продифференцируем функцию (4.21) по у:

Используя второе равенство (4.20), можно записать:

.

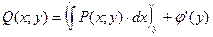Отсюда

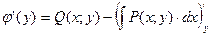. (4.22)

В равенстве (4.22) левая часть зависит от у. Покажем, что и правая часть равенства зависит только от у.

Для этого продифференцируем правую часть по x и убедимся, что производная равна нулю. Действительно,

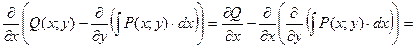
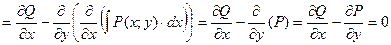
в силу условия (4.19).

Из равенства (4.22) находим :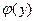

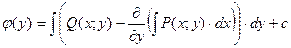, c - const.

Подставляя найденное значение для 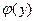в равенство (4.21), находим функцию

и(х; у) такую, что du(x; у) = Р(х; у)·dx + Q(x; у)·dy.

Таким образом, при решении ДУ вида (4.17) сначала проверяем выполнение условия (4.19). Затем, используя равенства (4.20), находим функцию и(х;у). Решение записываем в виде (4.18).

Пример 4.11. Решить уравнение .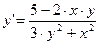

Решение: Запишем уравнение в дифференциальной форме:

.

Здесь Р(х;у) = 2ху - 5, Q(x;y) = Зу² + х². Проверяем выполнение условия (4.19):

; ; .

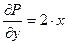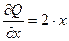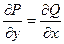Следовательно, данное уравнение есть уравнение в полных дифференциалах. Условия (4.20) будут здесь выглядеть так

, .

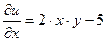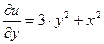Отсюда имеем

;

.

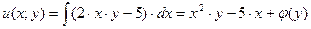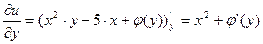Далее

, ,

, .

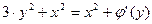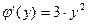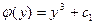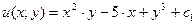Общим интегралом является 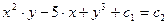, или ,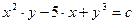

где .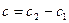

Если условие (4.19) не выполняется, то ДУ (4.17) не является уравнением в полных дифференциалах.

Однако это уравнение иногда можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию t(x; у), называемую интегрирующим множителем.

Чтобы уравнение 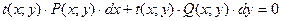было уравнением в полных дифференциалах, должно выполняться условие

.

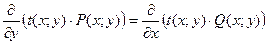Выполнив дифференцирование 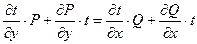и приведя подобные слагаемые, получим

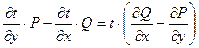. (4.23)

Для нахождения t(x; у) надо проинтегрировать полученное ДУ в частных производных. Решение этой задачи не простое. Нахождение интегрирующего множителя может быть упрощено, если допустить существование t как функции только одного аргумента х либо только у. Пусть, например, t = t(x). Тогда уравнение (4.23) принимает вид

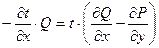, или .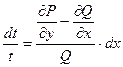

Отсюда

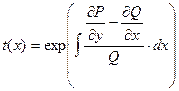. (4.24)

При этом выражение 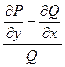должно зависеть только от х.

Аналогично получаем, что если t = t(y) (t не зависит от x), то

,

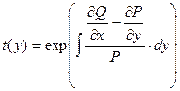а подынтегральное выражение должно зависеть только от у.

Пример 4.12. Решить уравнение .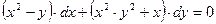

Решение: Здесь 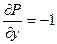; ; 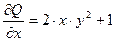т.е. .

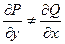Однако 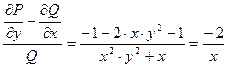зависит только от х.

Следовательно, уравнение имеет интегрирующий множитель, зависящий только от х, выражение которого может быть получено при помощи формулы (4.24). В нашем случае получим, что

.

Умножая исходное уравнение на 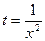, получаем:

,

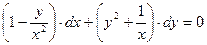т. е. уравнение в полных дифференциалах!!! Решив его, найдем, что общий интеграл заданного уравнения имеет вид

.

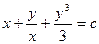Дата добавления: 2015-06-04