Методы определения оптимальных стратегий

1. Простейший метод состоит в нахождении седловой точки для чистых стратегий. Если такая седловая точка существует, то две чистые стратегии, которые к ней приводят, являются оптимальными.

2. Для уменьшения размерности игры используется доминирова­ние строк и столбцов.

Говорят, что k -я строка матрицы R доминирует i -ю строку (т.е. од­на чистая стратегия доминирует другую), если

при всех j.

Аналогично l -й столбец доминирует j -й столбец, если

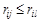при всех i.

Заметим, что доминирующая стратегия никогда не хуже, а в неко­торых случаях и лучше, чем доминируемая. Игроку невыгодно использо­вать доминируемую стратегию, и она не должна войти в оптимальную смешанную страте­гию. Это позволяет при решении игры все доминируе­мые строки и столбцы отбросить, т.е. уменьшить размеры матрицы.

Пример

Рассмотрим игру с матрицей

.

Вторая строка доминирует третью. Исключение третьей строки приводит к матрице

.

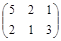Первый столбец в этой урезанной матрице доминирует второй. Исключе­ние второго столбца приводит к матрице

.

Найдя решение полученной игры, легко получить решение ис­ход­ной игры, приписав исключенным строкам и столбцам нулевые вероят­ности.

3. Существуют простые процедуры получения решения игр ма­лой размерности. Рассмотрим один из них на примере игры 2´2.

Пример

Рассмотрим игру с платежной матрицей

.

Эта игра не имеет решения в чистых стратегиях, так как

.

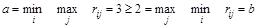Будем искать решение этой игры в смешанных стратегиях.

Пусть p и q – вероятности выбора игроками А и Б, соответст­вен­но, первой чистой стратегии. Тогда 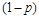и (1-q) – вероятности выбора ими вто­рой чистой стратегии.

Математическое ожидание результата .

Для определения оптимальной стратегии игрока А нужно найти

.

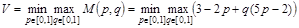Сначала при фиксированном значении p необходимо найти макси­мум по q, а для этого разобьем область изменения p на два интервала [0,0.4] и [ 0.4,1] знакопостоянства выражения (5p-2) и решим эту задачу на каждом из этих интервалов.

;

Итак, мы определили, что оптимальной для игрока А будет сме­шан­ная стратегия, при которой первая чистая стратегия выбирается им с вероятностью (или частотой) 0,4, а вторая - с вероятностью 0,6. Цена игры - 3,2.

Аналогично задача решается и для игрока Б.

С ростом размерности матрицы платежей сложность задачи замет­но воз­растает.

4. Для решения больших игр предложено несколько методов. Наи­бо­лее распространенным является определение опти­маль­ной стра­те­гии мето­да­ми линейного программирования.

Теорема. Каждой матричной игре m´n с платежной матрицей Rэквивалентна следующая пара двойственных задач линейного програм­мирования:

минимизировать целевую функцию при условиях

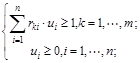(1)

максимизировать целевую функцию при условиях

(2)

Составляющие оптимальных смешанных стратегий игры 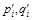и цена игры V связаны с компонентами оптимальных планов задачи ЛП со­от­но­шениями

(3)

Доказательство

Оптимальная стратегия должна обеспечить игроку А проиг­рыш, не боль­ший V при любом поведении противника. В частности, если игрок Б бу­дет использовать любую чистую стратегию, средний проигрыш не должен пре­высить V, т.е. должны выполняться следующие неравенства

(4)

Допустим, что все элементы матрицы платежей R положительны. Этого всег­да можно добиться, прибавив ко всем элементам матрицы достаточно боль­шое положительное число М; при этом цена игры уве­ли­чит­ся на М, а оп­тимальные стратегии не изменятся.

Тогда V>0 и, разделив неравенства (4) на V, получим

(5)

где

Так как , то .

Гарантированный проигрыш игрока А - V нужно миними­зи­ро­вать, т.е. - максимизировать.

Итак, мы доказали, что задача нахождения оптимальной страте­гии игрока А сводится к задаче линейного программирования (2) с m пере­менными и n ограничениями. Зная оптимальные значения , опти­мальную стратегию p и цену игры V можно найти по формулам (3).

Аналогично доказывается, что задача нахождения оптимальной стратегии игрока Б сводится к задаче линейного программирования (2).

Итак, вместо решения матричной игры можно решать эквива­лент­ную ей пару задач линейного программирования.

Справедливо и обратное утверждение: для любой задачи линейного программирования может быть построена эквивалентная ей задача теории игр.

Дата добавления: 2015-06-04