Эпюры внутренних усилий при растяжении-сжатии, кручении и изгибе

ОБЩИЕ ОРГАНИЗАЦИОННО-МЕТОДИЧВСКИЕ УКАЗАНИЯ

Методические указания к практическим занятиям составлены в соответствии с рабочей программой курса "Сопротивление ма­териалов".

Настоящие методические указания содержат теоретические сведения по наиболее трудным для усвоения темам курса, примеры решения типовых задач, варианты заданий для индивидуальной работы.

Задачи решается в буквенном виде, числовые данные подставля­ются лишь в окончательные выражения для искомых челичин. Реше­ние сопровождается вычерчиванием соответствующих схем, графи­ков.

Необходимые вычисления выполняются с помощью кальХулятора.

Внутренние силовые факторы (ВСФ) вычисляются на основе метода сечений. Эпюрами ВСФ называют графики изменения величины соответствуюшего ВСФ по длине бруса. Контроль пра­вильности построения эпюр проводится на основании дифференци­альных зависимостей между распределенной нагрузкой q и по­перечной силой Q (продольной силой N ) и изгибающим моментом М. Более подробно об этом можно прочитать в конспекте лекций или одном из рекомендуемых учебников.

Ниже приводятся примеры построении эпюр продольных сил N, крутящих моментов М_k поперечных сил Q и изгибающих момен­тов M.

Если брус загружен треугольной нагрузкой, то подход к вычислению ВСФ такой же, как и для случая равномерно распреде­ленной нагрузки:

1) находят равнодействующую (она равна площади, занимаемой нагрузки);

2) равнодействующее усилие проходит через центр тяжести этой площади.

Рассмотрим треугольную нагрузку и определим поперечную силу и изгибающий момент.

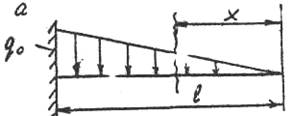
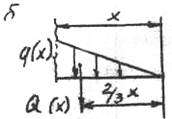
Рис 1.

На расстоянии x от свободного конца (рис. 1,а) проведем произвольное сечение. Равнодействующее усилие Q(x) будет приложено в центре тяжести треугольника (рис. 1,6) - в точке пересечения медиан (на расстояния 2/3 длины, отсчитываемой от острого угла).

Величина Q(x) равна площади треугольника:

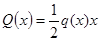
Произвольное значение распределенной нагрузки q(x) находим из подобия треугольнико через заданную величину q₀ рис 1.а.

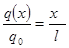
откуда

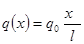
Следовательно,

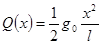
В соответствии с правилом знаков Q(x)>0, Находим изгибающий момент:

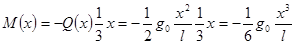
В случае трапециидальной нагрузки ее разбивают треугольную и прямоугольную (рис. 2).

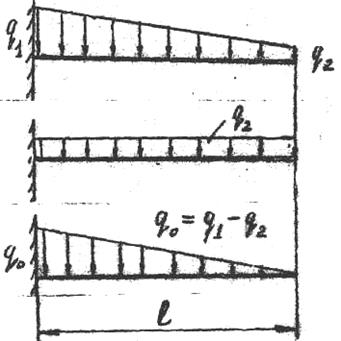
Рис. 2

Рассмотрим примеры построения ЭПЮР ВСФ.

Задача 1. Построить эпюру продольных сил для бруса, загруженного так как показано на рис. 3, и указать положение опасных сечений

Решение. Разбиваем брус на участки, начиная со свободного конца, и для каждого участка составляем выражение величин N. Границы участков определяются сечениями, где приложены внешние нагрузки. Правильность построения эпюры N проверяют по «скачкам»: «скачок» в эпюре N должен быть равен величине сосредоточенной силы, приложенной в соответствующем сечении.

Сечение 1-1 (рис.3) 0<=x₁<=4a

N₁=2P+qx₁=2qa+qx₁,

при x₁=0, N₁=2qa, при x₁=4a, N₁=2qa+4qa=6qa

Сечение 2-2 (рис.3) 4a<=x₂<=7a

N₂=2P+q4a-4P=2qa+4qa-4qa=2qa = const

Сечение 3-3 (рис.3) 0<=x₃<=5a

N₃=2P+q4a-4P-3Р-qx₃=2qa+4qa-4qa –3qa - qx₃=-qa - qx₃

при x₃=0, N₃= -qa - 0 = -qa

при x₃=5a, N₃= -qa – 5qa = -6qa

Из эпюры N видно, опасными поперечными сечениями будут сечения, где N₁=2qa+4qa=6qa – участок 1 и N₃= -qa – 5qa = -6qa участок 3. В первом случае имеем максимальное растягивающее, во втором максимальное сжимающее усилия.

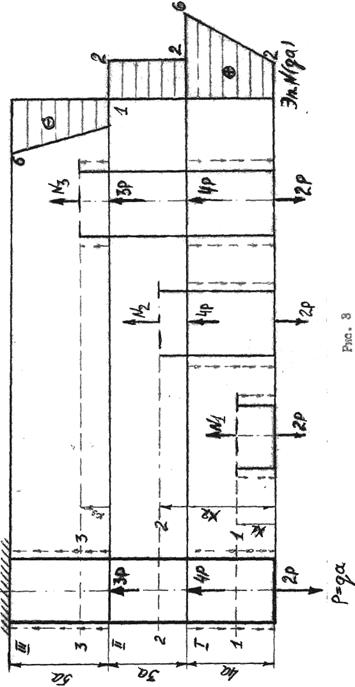
Задача 2. Построить эпюру крутящих моментов для вала нагруженного так как показано на рис. 4, и указать положение опасных сечений.

Решение. Вал круглого поперечного сечения вращается с постоянной угловой скоростью w=const. На вал насажены три шкива с внешними монетами: М₁ =50 кН·м, М₂ =17,50 кН·м, и М₃ (модуль и направление вращения М₃ по условию задачи не заданы). Диаметры вала на участках I и 2 различны: d₁=2d₂.

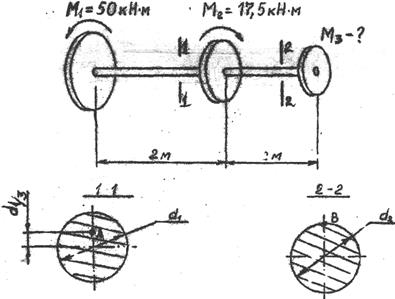
Рис. 4

Крутящий момент М_К это внутренний силовой фактор, возникающий в любом сечении вала при кручении.

Величина и направление крутящего момента зависят от значений внешних моментов, приложенных к валу.

Знаки Крутящих моментов проще определять по направлению внешних моментов.

Условимся считать крутящий момент положителдьным, если при взгляде со стороны сечения внешний момент направлен против хода часовой стрелки.

Для построения эпюры крутящих моментов условно разобьем вал иа участки и воспользуемся методом сечения.

Рассмотрим первый участок слева, изобразив отдельно отсеченную часть {рис. 5).

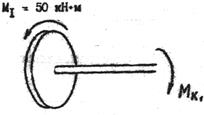Рис. 5

Внешний момент М₁ уравновешивается крутящим моментом M_К1, т.е M_К1 = M₁ = 50 кН·М.

Сделав сечение на втором участке и рассмотрев равновесие отсеченной части (рис. б), получим:

M₁- M₂- M_К2=0

M_К2= M₁- M₂=50-17.5=32.5кН·м

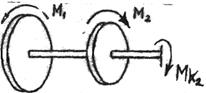
Рис. 6

По полученным значениям. M_К2 и M_К1построим эпюру M_К (рис 7.)

Так как M_К2 и M_К1постоянны, то эпюра ограничена прямыми линия­ми, параллельными оси вала.

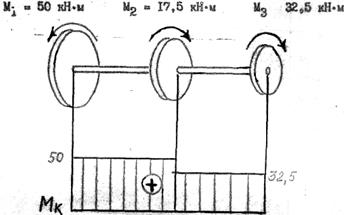Рис. 7

«Скачки» на эпюре М_К равны приложенным в соответствующих сечениях вала внешним моментам.

Следовательно, внешний мемент М₃ = 32,5 кН·м скручивает вал по часовой стрелке.

Значение и направление М₃ можно определить и до построения эпюры М_к исходя из того, что для вала, вращающегося с постоянной угловой скоростью сумма всех внешних моментов равна «0». Чтобы записать условие равновесия, произвольно зададимся направлением вращения М₃ по час овой стрелке.

Условие равновееия:

M₁- M₂- M₃ =0

отсюда M₃ = M₁- M₂ =50 –17.5= 32,5.

Тaк как значение получено со знаком "плюс", значит, первоначально выбранное направление для М₃ соответствует действительности.

Если в результате расчета получается отрицательная величииа, то первоначально выбранное направление необходимо изменить на противоположное.

Зная направление и значение M₃, строим эпюру крутящих моментов.

Опасными течениями вала будут сечени I-I и 2-2 (рис, 4), так как в сечегии 1-1 действует наибольший круутящий момент, а в сечении 2-2 диаметр вала меньше, чем в сечении I-I.

3 а д а ч и 3 и 4. Для балок, загруженных так, как показано на рис. 8 и 9, построить эпюры М и Q и указать положения опасных сечений.

Решение. В общем случае плоского прямого изгиба в поперечных, сечениях брусавозникают два внутренних силовых фактора: поперечная сила Q и изгибащий момент M.

Поперечная сила Q равна алгебраической сумме проекций внешних сил на ось, перпендикулярную оси балки, изгибающий момент М - алгебраичеокой сумме моментов всех внешних сил, расположенных по одну сторону, от сечения относительно центра тяжести рассмативаемого сечения.

Графики изменения Q и M по длине балки являютсясоответ­ственно эпюрой поперечных сил и эгидой изгибающих моментов.

Для определения знаков М и Q приняты специальные правила:

при рассмотрении правой части положительньми является поперечная сила, направленная вниз, и изгибающий момент, направленный против хода часовой стрелки;

при рассмотрении левой части положительными считается попе­речная сила, направленная вверх и изгибающий момент, направ­ленный по ходу часовой стрелки

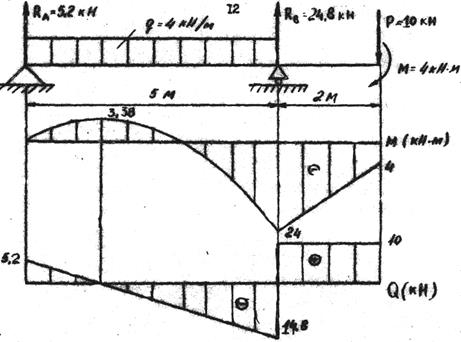Рис. 8

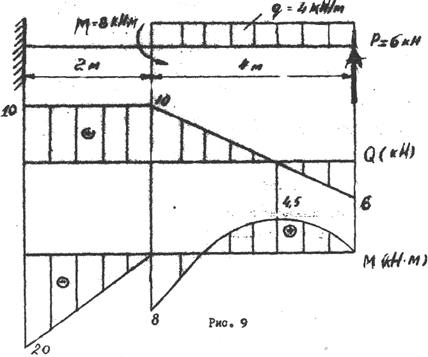Рис. 9

Эти правила можно проиллюстрировать следующим рисунком:

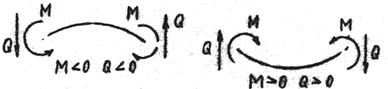
контроль правильности построения эпюр М и Q осуществляется с помощью дифференциальных зависимостей при изгибе.

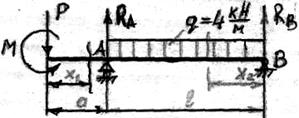
Построим эпиры М и Q, для балки, схема которой приведена на рис. 8.

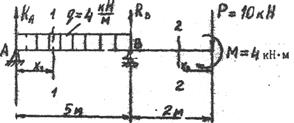
Прежде чем приступить к построению эпюр для балок на двух опорах необходимо определить опорные реакции.

Для этого составим уравнения равновесия для балки, освобожденной от связей:

Sm_A= - P7 – M - q5·5/2+R_B5=0

Sm_B= - R_A5 – P2-M+q5·5/2 =0

Подставим числовые значения и найдем величины R_A и R_B.

R_B =(10·7+4+50)/5 = 24.8kH

R_A= (50-20-4)/5 = 2.2kH

Проверку правильности найденных значений опорных реакций производим по третьему уравнению равновесия - сумме проекций всех сил на вертикальную ось балки SУ=0

SУ= R_A + R_B - q·5-P=5.2+24.8-4·5-10=0

Уравнение обращается в тождество. Следовательно, опорные реакции по величине и направлению определены правильно.

Для построения эпюр М и Q применим метод сечений, Балка состоит из двух участков первый участок расположен от точки A до точки В, второй от точки С до точки В. На первом участке произвольно выбираен сечение на расстоянии Х₁ от опоры А.

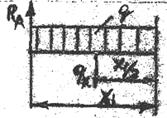
составим выражения М и Q для рассматриваемого первого участка 0<=Х₁ <=5m

Q₁=R_A – qx₁

M₁=R_AX₁ – qx₁x₁/2= R_AX₁ – 0.5qx₁²

На рисунке справа приводится правило знаков длярассматриваемой левой части балки. Равнодействующая распределенной q равна qx₁ и приложена на расстоянии x₁ /2 от рассматриваемого сечения в центре тяжести прямоугольника.

Для построения эпюры Q достаточно найти два значения, так как зависимость Q= Q(х) является линейной.

X₁ =0, Q=R_A

X₁ =5м, Q= 5.2-4·5= -14.8 кН

Поперечная сила (в пределах участка I) меняет знак с "плюса" на «минус», следовательно в сечении, где Q проходит через 0, имеем М =М_мах

Определим точку экстремума:

Q₁=R_A – qx₁=0, х₁=R_A/q=5,2/4=1.3м

Эпюра M ограничена параболической кривой X=0, М₁=0.

X₁ =4м, М₁= 5.2·4-4·16/2= -11.2 кН·м

X₁ =1,3м, М₁= 5.2·1.3-4·1.3²/2= 3.33 кН·м

Рассмотрим второй участок: 0<=Х₂ <=2m

Q₂=Р=10кН=const,

М₂= -P·X₂ –M;

X₂=0, М₂= -4 кН·м

X₂=2m, М₂= -10·2 – 4= -24 кН·м

По полученным данным строим эпюры М и Q (рис.8).

Для контроля правильности построения эпюр воспользуемся выводами, полученными из дифференциальных зависимостей.

Первый участок балки загружен сплошной равномеоно распреде­ленной нагрузкой, поэтому эпюра М ограничена параболической кривой, а эпюра Q- наклонной прямой.

Сплошная нагрузка направлена вниз, т.е 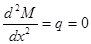, следовательно, эпюра М очерчена кривой, имеющей выпуклость вверх.

Второй участок свободен от равномерно распределенной нагрузки (q= 0), следовательно dQ/dx =0, Q=const т.е. на этом участке эпюра Q ограничена прямой, параллельной оси X, а эпюра М - наклонной прямой.

"Скачки" в сечениях под сосредоточенными силами равны соответствующим силам (рис. 8), а "скачок" в эпюре М равен моменту сосредоточенной пары сил.

На первом участке в сечении, где Q, переходит через нуль, М=М_мах.

Рассмотрим особенности построения эпюре М и Q для балки с защемленным концом (консоль). на рис 9.

Здесь так же как и в задаче 3, можно предварительно определить опроную рекцию и опорный момент и затем рассмотреть правую и левую части балки.

Однако для того, чтобы избежать вычислений, связанных с определением опорныхмоментов и реакций, рекомендуеися рассмотреть правую часть балки.

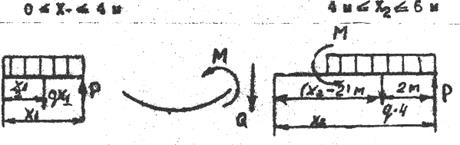
Q₁= -P + qx₁, Q₂= -P + q·4=const

M₁=PX₁ – 0.5qx₁²; M₂=PX₂ – q·4(x₂ –2) +M;

Подставив в формулы численные значения, строим эпюры М и Q так же как и в задаче 3 (рис. 9).

Для консольных балок эпюры строят аналогичным образом.

0<=Х₁ <=а; Q₁=-Р=const, М₁= -P·X₁ –M;

0<=Х₁ <= l; Q₂=-R_A+qx₂, М₂= R_B·X₂ – 0.5qx²;

В задаче 3 опасным сечением будет сечение над опорой В

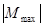=24кН·м, 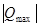=14.8кН,

Опасное сечение в задаче 4 - защемление;

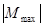=20кН·м, 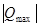=10кН,

Геометрические характеристики плоских сечений.

Прочность и деформация бруса зависят не только от поперечного сечения, но и от других геометрических характеристик сечения, основными из которых являются статические момненты сечения: осевые, полярный и центробежный момент инерции.

Оси, проходящие через центр тяжести сечения, называются ценральными осями.

При повороте сечения относительно некоторых осей осевые и центробежный моменты инерции изменяются.

Центральные оси, относительно которых центробежный моменты инерции равен нулю, называются главными центральными осями.

Осевые моменты инерции относительно зтих осей имеют экстремальные значения и называются главными центральными моментами инерции.

Дата добавления: 2015-06-30