Канонические формы представления ФАЛ

Задание ФАЛ с использованием контактных схем

Задание ФАЛ при помощи диаграмм Венна

Задание ФАЛ с использованием диаграмм двоичного решения

Диаграмма двоичного решенияявляется разновидностью корневого ориентированного графа. Она обеспечивает полное, краткое и простое описание сложных цифровых функций. На рисунке 2.7 приведена диаграмма двоичного решения для функции .

На рисунке 2.7 прямоугольники с цифрами 0 и 1 соответствуют окончательным значениям ФАЛ. Узлы, обозначенные кружками, соответствуют переменным, от которых зависит ФАЛ, а цифры у ветвей – значениям этих переменных. Диаграммы двоичного решения широко используются для анализа сложных функций, формирования тестов, задач верификации и т.д.

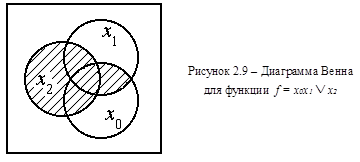
Диаграммы Венна, названные по имени священника Джона Венна [3], применявшего их в исследованиях по логике, являются графическим представлением, демонстрирующим соотношения между множествами. На основе соответствия между теорией булевой алгебры и теорией множеств диаграммы Венна очень полезны для визуального представления аксиом и законов булевой алгебры, однако их не следует использовать для построения доказательств тождеств, поскольку большинство общих положений эти диаграммы показать не могут. На рисунке 2.8 приведены диаграммы Венна для констант «0», «1» и элементарных функций логического умножения, сложения и инверсии. Область, ограниченная кружком на рисунке, соответствует одной переменной. На рисунке 2.9 представлена диаграмма Венна для функции .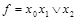

Контактная схемаможет рассматриваться как техническая модель логических выражений. Одну из первых моделей предложил в 1910 году физик П.С. Эренфест [3], в которой использована аналогия между высказываниями и электрическими контактами, поскольку и те и другие имеют двоичную природу. На рисунке 2.10 приведены контактные модели для констант 0, 1 и элементарных функций логического умножения, сложения и инверсии. Обозначение U _ип на рисунках указывает на положительный полюс источника питания.

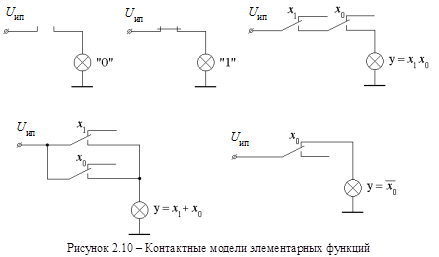
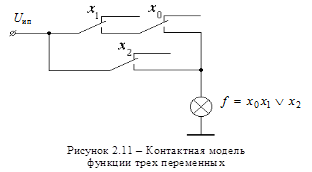
На рисунке 2.11 представлена реализация на контактах функции .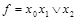

При минимизации ФАЛ часто приходится представлять исходные выражения в нормальном (каноническом) виде, т.е. пользоваться так называемыми каноническими формами ФАЛ [1]. Рассмотрим их подробнее.

К каноническим (общепринятым) формам представления ФАЛ относятся:

1) ДНФ (дизъюнктивная нормальная форма);

2) СДНФ (совершенная дизъюнктивная нормальная форма);

3) КНФ (конъюнктивная нормальная форма);

4) СКНФ (совершенная конъюнктивная нормальная форма).

Определение. Элементарной конъюнкцией называется конъюнкция (логическое умножение) любого числа различных независимых переменных, входящих в данную конъюнкцию с инверсией или без нее не более одного раза. Например,

Определение. Элементарной дизъюнкцией называется дизъюнкция (логическое сложение) любого числа различных независимых переменных, входящих в данную дизъюнкцию с инверсией или без нее не более одного раза. Например,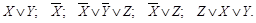

Определение. Дизъюнктивной нормальной формой называется дизъюнкция любого числа элементарных конъюнкций. Например,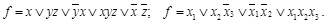

Совершенная ДНФ содержит в каждом члене все аргументы или инверсии заданной функции.

Например,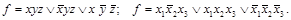

Определение. Конъюнктивной нормальной формой называется конъюнкция любого числа элементарных дизъюнкций. Например,

Совершенная КНФ содержит в каждой скобке все аргументы или их инверсии.

Например .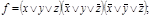

Формы СДНФ и СКНФ используются в процессе синтеза ДУ для перехода от табличной формы представления функций алгебры логики к аналитической, а также являются базовыми для различных методов минимизации, особенно связанных с применением персональных компьютеров.

Для получения СДНФ по ТИ необходимо проанализировать значение функции на всех наборах аргументов. Каждое единичное значение функции дает один член (одну конъюнкцию) в формуле СДНФ. Все члены (все конъюнкции) соединяются между собой знаками дизъюнкции. Таким образом, число конъюнкций равно числу единиц в значении функции в ТИ.

Каждая конъюнкция состоит из произведения аргументов функции, а каждый аргумент в формуле записывается без инверсии, если в ТИ он равен единице, или с инверсией, если в ТИ он равен нулю.

Например для таблицы 3.1, СДНФ будет иметь следующий вид: 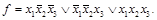Для перехода от ДНФ к СДНФ необходимо добавить к каждому члену (конъюнкции) недостающие аргументы, используя закон дополнительности до единицы. Например,

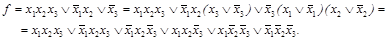
Форма ДНФ является упрощенной, т.е. позволяет построить схему с меньшим числом элементов, чем при форме СДНФ.

При переходе от СДНФ к ДНФ можно использовать для упрощения формулы законы АЛ или любые другие способы минимизации функций.

Форма СКНФ также получается по ТИ. В СКНФ присутствует столько скобок, сколько нулей имеет функция в ТИ. Каждая скобка соединяется знаком конъюнкции.

Для получения аргументов в скобках используются следующие правила.

1) Если значение аргументов в ТИ равно нулю, то в формуле этот аргумент записывается без инверсии.

2) Если же в ТИ значение аргумента равно единице, то он записывается в формулу с инверсией.

Все аргументы в скобке соединяются между собой знаками дизъюнкции. Для таблицы 3.1 СКНФ будет иметь следующий вид:

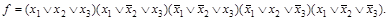
Для перехода от КНФ к СКНФ необходимо, используя законы и правила АЛ (в основном закон дополнительности до нуля), добавить к каждому члену (в каждой скобке) недостающий аргумент.

Например,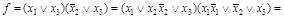

Большая часть методов минимизации ориентирована на получение минимальной дизъюнктивной нормальной формы (МДНФ).

Определение. Число переменных, входящих в конъюнкцию дизъюнктивной нормальной формы, называется рангом конъюнкции. Для СДНФ ранг конъюнкции равен числу аргументов функции.

Определение. Две конъюнкции называются соседними, если они различаются значением только одной переменной. Например,

Определение Конъюнкция (n – 1) переменной, полученная в результате склеивания соседних конъюнкций (конституентов) по закону склеивания называется минтермом (n – 1) ранга; конъюнкция (n – i) переменных, полученная склеиванием соседних минтермов [ n – (i – 1)]-го ранга, называется минтермом (n – i)-го ранга.

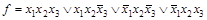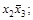
Например, в выражении после применения закона склеивания получатся следующие минтермы 2-го ранга: и функция после первой итерации применения закона склеивания будет состоять из дизъюнкции минтермов 2-го ранга 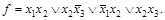Применив закон склеивания к полученной функции второй раз, получим минтерм 1-го ранга x ₂. Причем, этот минтерм будет реализовывать ту же ТИ, что и исходная функция, т.е.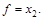

Определение. Конституенты (минтермы) функции, к которым не применима операция склеивания, называются простыми или первичными импликантами.

Определение. Простой импликант называется существенным, если он образован склеиванием таких конституентов, что по крайней мере для одного из них эта операция была единственной.

Определение. ДНФ ФАЛ, составленная из простых импликантов, некоторые члены которой могут быть избыточными и удалены без нарушения эквивалентности исходной функции, называется сокращенной.

Определение. ДНФ ФАЛ называется тупиковой, если ни один ее член не может быть удален без нарушения эквивалентности исходной функции. К минтермам тупиковой ДНФ (ТДНФ) операция склеивания неприменима.

Определение. ТДНФ называется минимальной, если она содержит наименьшее число вхождений переменных по сравнению с другими ТДНФ. Минимальная форма функции обязательно содержит существенные импликанты.

Можно выделить два направления в решении задачи минимизации.

Первое состоит в отыскании простых импликантов, построении из них тупиковых форм и определении путем перебора минимальной ДНФ.

Второе направление заключается в нахождении всех существенных импликантов, отыскании недостающих для реализации заданной функции простых импликантов и построении ТДНФ.

Каждое из обоих направлений включает целый ряд методов. Рассмотрим некоторые из них.

Дата добавления: 2015-07-02