Интегралы, зависящие от параметра

Мичуринск-Наукоград 2012

Реферат

«Параметрические интегралы»

Выполнил:

Студент

экономического

факультета

21 Э группы

Бахарев А.С

Проверил:

1. Непрерывность интеграла от параметра

Рассмотрим интеграл

F(y) =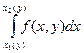

для области вида

Где f определена в области D (замкнутая), x₁(y), x₂(y) непрерывные функции, определенные на [c,d].

Теорема. Если f непрерывна на D, x₁(y), x₂(y) непрерывны на [c,d], то F(y) непрерывна на [c,d].

Доказательство. Функция f доопределим на прямоугольнике [a,b]´ [c,d] содержащем область D, как показано на рисунке,следующим образом: положим f(x,y) = f(x₁(y), y) при фиксированном y Î [c,d] и "xÎ[a, x₁(y)], аналогично в правой части области f(x,y) = f(x₂(y), y) при y Î [c,d] и "xÎ[ x₂(y), b]. Доопределенную функцию по прежнему будем обозначать f(x,y). Эта функция будет непрерывна на [a,b]´ [c,d].

Далее |F(y+Dy) - F(y)| = 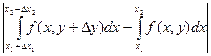= £ + + £ M|Dx₁|+(b - a)e + M|Dx₂|.

Здесь используется ограниченность функции f и ее равномерная непрерывность.

Определение. Пусть функция f(x,y) определена на [a,b] для любого yÎY. Говорят, что f(x,y) равномерно сходится к g(x) на [a,b] при y®y₀ если

"e >0$d >0"xÎ[a,b]"yÎU_d(y₀): |f(x,y) - g(x)|<e.

Можно доказать, что если f(x,y) непрерывна иравномерно сходится к g(x) на [a,b] при y®y₀ , то функция g(x) непрерывна на [a,b].

Доказательство. Выпишем неравенства

|g(x)-g(x₀)|=| g(x)-f(x,y) +f(x,y)-f(x₀,y)-g(x₀)+ f(x₀,y)|£ | g(x)-f(x,y)|+ |f(x,y)-f(x₀,y)|+ |g(x₀)- f(x₀,y)|. Для заданного e сначала выбираем d окрестность точки x₀ так, чтобы в этой окрестности |f(x,y)-f(x₀,y)|< e для любых y из некоторой окрестности точки y₀. Это можно сделать в силу равномерной непрерывности функции f(x,y). Величины | g(x)-f(x,y)|, |g(x₀)- f(x₀,y)| можно сделать также < e выбором ещё меньшей окрестности точки y₀ для всех x в силу равномерной сходимости f(x,y) к g(x).

Теорема. Если f(x,y) непрерывна и равномерно сходится к g(x) на [a,b] при y®y₀, то

.

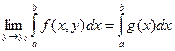Доказательство. 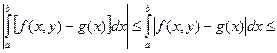|b - a|e.

1. Интегрирование интегралов зависящих от параметра

Предположим, что область является одновременно и областью типа А и В. Из формул выражения двойного интеграла через повторные следуют следующие формулы

F(y) =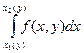

2. Дифференцирование интегралов, зависящих от параметра

Теорема (Лейбниц). Если f и непрерывны в [a,b]´ [c,d], то F(y) =

дифференцируема на [c,d] и .

Доказательство.

= = , 0<q <1. Тогда

£ .

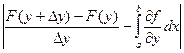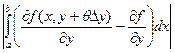Из этого неравенства и равномерной непрерывности функции следует требуемое утверждение.

Рассмотрим область типа В, указанную на рисунке и функцию f, определенную на прямоугольнике [a,b]´ [c,d], содержащем область D.

Теорема. Если f и ее производная непрерывны на [a,b]´ [c,d], x₁(y), x₂(y) имеют непрерывные на [c,d] производные, то F(y) = 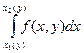также имеет производную

+ - .

Доказательство. Рассмотрим функцию Ф(y,u,v) = . Для нее существуют непрерывные частные производные (не очевидным является непрерывность функции ). Дифференцируя сложную функцию F(y) = 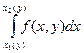= Ф(y, x₁(y), x₂(y)) получим требуемое равенство. Непрерывность функции = следует из равномерной непрерывности функции .

§2. Несобственные интегралы, зависящие от параметра

3. Равномерная сходимость несобственного интеграла от параметра

Рассмотрим интеграл

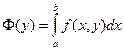(1)

, yÎY.

Предположим, что при некоторых y интеграл (1) является несобственным. Так, если и при некотором y интеграл (1) имеет единственную особенность в b, то условием сходимости интеграла (1) будет существование конечного предела

.

Если при заданном y интеграл сходится, то для любого hÎ[a,b) интеграл (называемый остатком) будет существовать и условие сходимости можно записать в виде . В случае расходимости этого интеграла, естественно считать, что условие не выполнено. Таким образом, условие сходимости будет в дальнейшем записываться в виде

.

Определение. Сходящийся на Y интеграл называется равномерно сходящимся на Y, если

"e >0$d >0"hÎ(b-d,b)"yÎY: 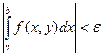(для интеграла 2-го рода)

"e >0$M"hÎ(M,+µ)"yÎY: (для интеграла 1-го рода)

Признак Вейерштрасса равномерной сходимости (для интеграла 2-го рода)

Если $g(x) на [a,b), интегрируемая на любом [a, h), hÎ(b-d,b) такая, что

1) |f(x,y)| £ g(x), a £ x < b, "yÎY

2) 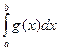сходится,

то интеграл (1) сходится равномерно на Y.

Утверждение следует из неравенств .

Теорема: Пусть и f(x,y) определена и непрерывна на [a,b) по x для всех yÎY. Если для любых h функция f(x,y) равномерно сходится к g(x) на [a,b-h] при y®y₀, интеграл равномерно сходится на Y, сходится. Тогда

.

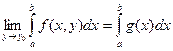Доказательство.

= .

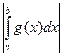можно сделать сколь угодно малым в силу равномерной сходимости функции f(x,y) к g(x). Интеграл можно сделать сколь угодно малым в силу равномерной сходимости интеграла . Интеграл можно сделать сколь угодно малым в силу сходимости интеграла .

Критерий Коши равномерной сходимости. Для равномерной сходимости интеграла необходимо и достаточно, чтобы

"e >0$d>0" y Î Y"h¢,h¢¢Î(b-d,b): .

Достаточность. При выполнении условия для " y Î Y"h¢,h¢¢Î(b-d,b) можно перейти к пределу при h¢¢ ® b. Тогда для " y Î Y"h¢Î(b-d,b): , что означает равномерную сходимость интеграла .

Необходимость. Имеем "e >0$d>0" y Î Y"hÎ(b-d,b): 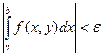. Тогда при h¢,h¢¢Î(b-d,b) будет выполнено .

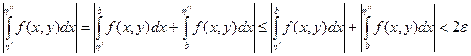4. Непрерывность интеграла от параметра

Теорема 2. Если f(x,y) определена и непрерывна на [a,b)´[c,d], интеграл F(y) = сходится равномерно на [c,d], то этот интеграл является непрерывной функцией.

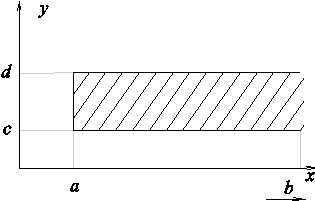
Доказательство.

|F(y+Dy) - F(y)| = £ + + .

Второй и третий интегралы могут быть сделаны меньше заданного e выбором h в силу равномерной сходимости интеграла . После выбора h первый интеграл может быть сделан меньше заданного e выбором достаточно мелкого разбиения в силу равномерной непрерывности функции.

5. Интегрирование интегралов зависящих от параметра

Теорема. Если функция f(x,y) определена и непрерывна на [a,b)´[c,d], интеграл F(y) = сходится равномерно на [c,d], то

= = .

Доказательство. Для любого h в разумных пределах

= . Отсюда следует требуемое утверждение, если учесть, что сходится равномерно на [c,d] к при h®b.

Эту теорему можно обобщить

Теорема. Если функция f(x,y) определена и непрерывна на [a,b)´[c,d), интеграл сходится равномерно на " [c,h], интеграл сходится равномерно на " [a,x] и существует один из повторных интегралов

,

, то существует и другой и выполняется равенство

= .

Без доказательства.

6. Дифференцирование интегралов, зависящих от параметра

Лемма. Если функция f(x,y) непрерывна на [a,b)´[c,d], то сходимость интеграла эквивалентна условию для любой последовательности h_n®b сходится ряд .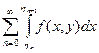

Аналогично для равномерной сходимости.

Теорема. Пусть функции f(x,y) и непрерывны на [a,b)´[c,d]. Если сходится для всех y а сходится равномерно на [c,d], то функция F(y) = непрерывна дифференцируема на этом отрезке и

.

Доказательство: Пусть h_n®b. Согласно лемме

F(y) = = , .

Далее применяется теорема о дифференцировании функционального ряда.

Пример. Гамма функция Эйлера Г(p) = , p > 0.

Непрерывность на (0, µ).

Рассмотрим два интеграла , .

1) £ 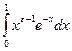, pÎ[e, 1). Признак Вейерштрасса.

- собственный для pÎ[1, ¥).

2) £ 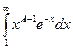, pÎ[1, A]. Признак Вейерштрасса.

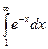£ , pÎ(0, 1].

Докажем формулу

(1)

Для этого сделаем замену x ® xy. G(p) = = = .

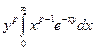2. Бета функция Эйлера В(p,q) = , p > 0, q >0.

Сделаем замену , dx = .

В(p,q) = = .

В(p,q) = (2)

3. Некоторые свойства функций Эйлера

Из формулы (1) следует, что

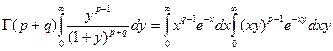, . Интегрируя, получим . Откуда, используя (2)

Г В(p,q) = Г Г .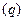

В(p,1-p) = Г Г = = .

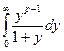Г(1) = 1, Г(p+1) = p Г(p).

Отметим, что из этой формулы следует, что Гамма функцию достаточно знать на интервале (0, 1/2).

Интеграл сходится равномерно на любом [e, A ], 0 < e < A. Поэтому интеграл можно дифференцировать по параметру. Рассмотрим интеграл .

В окрестности нуля |ln x| £ для e > 0 существует C₁(e).

В окрестности бесконечности |ln x| £ для e > 0 существует C₂(e).

Интеграл Г^(k)(p)= сходится равномерно на любом компакте. Это следует из оценок £ + 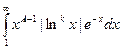, pÎ[e, A]. Здесь для степеней логарифма справедливы оценки:

В окрестности нуля интеграл сходится при 0<a<1, действительно т. к. x^b-aln^kx = .

В окрестности бесконечности сходится, действительно

x^A-1|ln ^k x| £ C x^A т. к. и кроме того .

4. Примеры вычисления несобственных интегралов, зависящих от параметра

Формула Фруллани. Функция f(x) непрерывна и интеграл существует для любого A > 0.

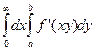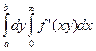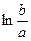= , = = = = =- f(0) .

= f(0) .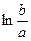

Интегрированием по частям вычисляются интегралы

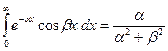, a ³ 0, , a ³ 0.

Другой способ: Положим g = -a + ib, , откуда и следуют указанные формулы.

Вычислить

.

, = +С.

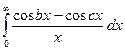= = Þ С = 0.

Интеграл Пуассона

I = .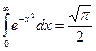

I ² = = = = = = .

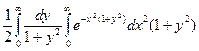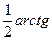
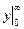Интеграл I = .

Интегрирование по частям I = = = .

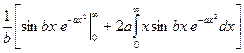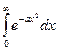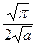= I, , I = C , I(0) = = = , I = .

Вычислить интеграл F(a,b) = 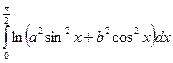, a>0, b>0 (1)

(2),

из (2) F(a,b) = 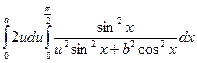+С(b).

= = =

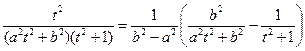
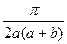
F(a,b) = +C(b)= +C(b).

p ln b = F(b,b)=p ln 2 + C(b), C(b) = p .

Дата добавления: 2015-07-02