Декомпозиция правил грамматики

ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ КС- И А-ГРАММАТИК

Напомним, что две грамматики G₁ и G₂ называются эквивалентными, если они порождают один и тот же язык (L(G₁)=L(G₂)). Одна из основных задач теории формальных языков - задача выбора наилучшей, по некоторым показателям, грамматики или автомата для описания того или иного языка.

Задача определения эквивалентности двух произвольных грамматик (автоматов) алгоритмически неразрешима. Однако, существуют некоторые преобразования, которые позволяют получить грамматику эквивалентную данной. Преобразования из недетерминированной формы в детерминированную, минимизация, сжатие и ускорение, рассмотренные в разделе 3, - примеры таких эквивалентных преобразований. Ниже будут рассмотрены еще некоторые преобразования, полезные для практики.

Пусть нам дана КС-грамматика G₁=(N,S,P,S).

Теорема 4.1. Если в КС-грамматике G₁ существуют правила Y ®aXb и X ®g, тограмматика G₂=( N,S,P È { Y®agb},S) эквивалентна G₁.

Доказательство. Проверим, что любая цепочка, выводимая в одной грамматике, выводима и в другой.

Пусть j Î L(G₁), тогда дерево вывода j в G₁ является деревом вывода j и в G₂. Обратно, пусть j Î L(G₂), следовательно существует некоторое дерево вывода j в G₂. Если при этом правило Y®agb не используется, то дерево вывода j в G₂ является деревом вывода j в G₁. Если же правило Y®agb использовалось при выводе j в G₂, то фрагмент вывода Y Þ agb заменяем на фрагмент

Y Þ aXb Þ agb.

В результате получим дерево, в котором используются правила только из P, то есть получим вывод цепочки в G₁. Следовательно, из j Î L(G₂) следует, что j Î L(G₁). 

Теорема 4.2. Пусть в грамматике G₁ имеется множество правил

{Y® a Xb, X® g₁, X® g₂,..., X® g_n}.

Тогда, заменив это множество на множество

{Y® ag₁b, Y® ag₂b,..., Y® ag_nb, X ® g₁, X® g₂,... X® g_n},

получим грамматику, эквивалентную G₁. И далее, если X ¹ S и других правил, которые имеют X в правой части нет, то группу правил X ® g _k, 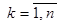можно удалить.

Доказательство. Многократно применяя теорему 4.1 в грамматику добавляем правила Y® ag_kb, где 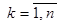. Удаление правила Y® aXb не приводит к потере выводимых цепочек, так как фрагмент дерева вывода Y Þ aXb Þ ag_kb можно заменить на YÞ ag_kb. ƒ

Пример 4.1. Рассмотрим фрагмент грамматики для описания числа

<число> ® <знак> <чбз>

<знак> ® + ½ -½ e

Здесь в соответствии с теоремой 4.2: Y - <число>, a - пустая цепочка, X - <знак>, b - <чбз> (число без знака), g₁ - +, g₂ - -, g₃ - e. Группу приведенных правил заменяем на правила

<число> ® + <чбз> ½- <чбз> ½ <чбз> ƒ

Теорема 4.3. Замена группы правил Y₁ ® a ₁Xb ₁ , Y₂ ® a ₂Xb ₂ ,... Y_m ® a _mXb_m, X ® g на правила Y₁ ® a ₁gb ₁ , Y₂ ® a ₂gb ₂ ,... Y_m ® a _mgb _m, X ® g, где других правил с нетерминалом X в левой части нет, приводит к эквивалентной грамматике. Если X ¹ S и других правил, которые имеют X в правой части нет, то правило X ® g можно удалить.

Доказательство здесь аналогично теореме 4.2. ƒ

Пример 4.2. Замена правил:

S ® AB. C ½ AB. ½ A. C ½ B. ½. C

A ® -

на правила:

S ® - B. C ½ - B. ½ -. C ½ B. ½. C

приводят к эквивалентной грамматике. ƒ

Теорема 4.4. Декомпозиция правил. Замена в грамматике G₁ группы правил

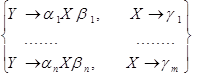на группу правил 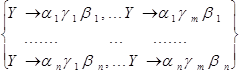, если

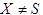и других 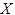в левых и правых частях правил грамматики нет, приводит к грамматике, эквивалентной G₁.

При декомпозиции n+m правил грамматики заменяется на n * m правил. ƒ

Пример 4.3. Рассмотрим КС - грамматику идентификатора, имеющую вид:

<И> ® <Б> ½ <Б> <И₁>

<И₁> ® <Б> ½ <Б> <И₁> ½ <Ц> ½ <Ц> <И₁>

<Б> ® a ½ b ½ c ½ ... ½ y ½ z

<Ц> ® 0 ½ 1 ½ 2 ½ ... ½ 8 ½ 9

В предложенной грамматике 42 правила. Проведем в ней декомпозицию по <Б> и по <Ц>. Получим новую грамматику, эквивалентную заданной.

<И> ® a ½ ... ½ z ½ a <И₁> ½ ... ½ z <И₁>

<И₁> ® a ½ ... ½ z ½ a <И₁> ½ ... ½ z <И₁> ½ 0 ½...½ 9 ½ 0<И₁> ½ ... ½ 9<И₁>

В результате получено 4*26=104 правил для букв и 2*10=20 правил для цифр, итого 124 правила. Правил стало больше, но вывод, а следовательно и разбор, будет короче. Нетрудно видеть, что рассмотренная декомпозиция позволила перейти от КС-грамматики идентификатора к А-грамматике. ƒ

Отметим в заключении параграфа, что все рассмотренные теоремы работают в обе стороны. Так n * m правил при композиции можно заменить на n+m правил. Иногда лучше иметь правил поменьше и компактно описывать язык; иногда, с целью повышения эффективности разбора, их количество необходимо увеличить.

Дата добавления: 2015-06-27