Приведение задачи линейного программирования к канонической форме

,,.

Виды задач линейного программирования

Задачи линейного программирования делятся на два вида: канонические (основные) и стандартные (симметричные).

Каноническая задача линейного программирования – это задача, в систему ограничений которой входят только линейные уравнения и условия неотрицательности выполняются для всех переменных, то есть

, , .

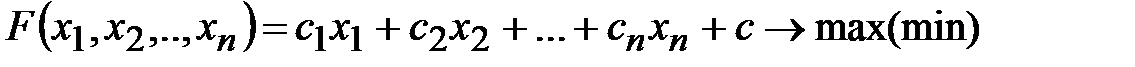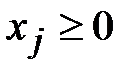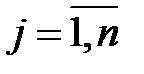Стандартная задача линейного программирования – это задача, в систему ограничений которой входят только линейные неравенства со знаком (со знаком 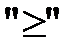), целевая функция стремится к максимуму (минимуму) и условия неотрицательности выполняются для всех переменных, то есть

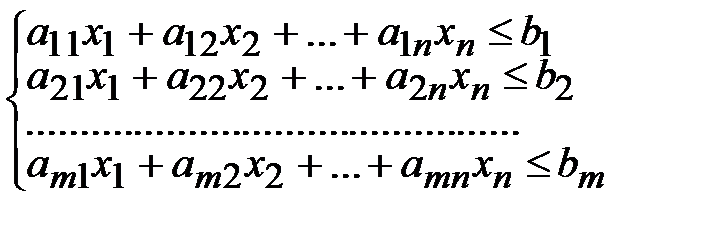
Любую задачу линейного программирования можно привести к канонической форме по следующему правилу:

1) если знак неравенства 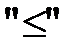, то балансовая переменная вводится со знаком плюс;

2) если знак неравенства 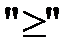, то балансовая переменная вводится со знаком минус;

3) в целевую функцию балансовые переменные не вводятся;

4) если на какую либо исходную переменную не наложено условие неотрицательности (например, на 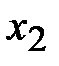), то ее можно представить в виде разности двух положительных переменных (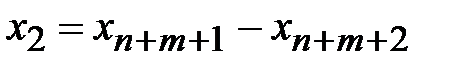) и выполнить соответствующую замену в исходной задаче.

Пример 3. Привести к каноническому виду задачу линейного программирования

, , .

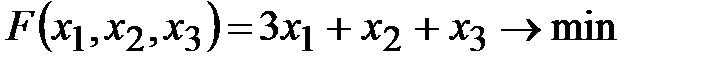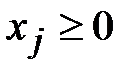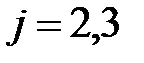Решение. Первое уравнение системы ограничений оставим без изменения. Во второе неравенство системы ограничений введем балансовую переменную со знаком плюс 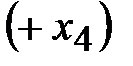, а во второе неравенство переменную со знаком минус 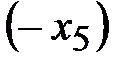. В целевую функцию эти переменные не вводятся. Так как на переменную 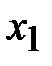не наложено условие неотрицательности, то заменим ее разностью двух положительных переменных 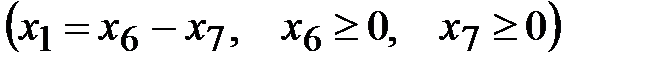. Выполним соответствующую замену в целевой функции.

Каноническая форма исходной задачи будет иметь вид:

, , .

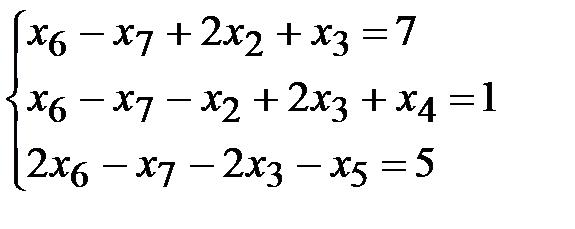
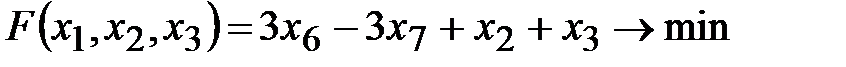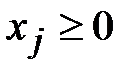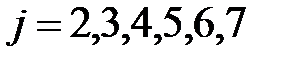Задания для решения в аудитории

1. Привести к каноническому виду задачу линейного программирования

, , .

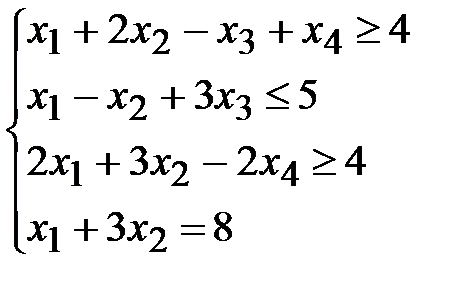
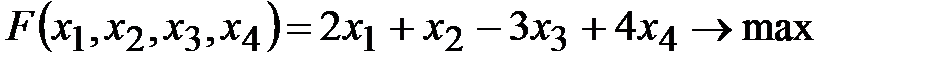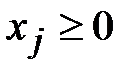Дата добавления: 2015-06-27