
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Особые случаи симплексного метода
Составление и преобразование симплексных таблиц
Алгоритм решения задач линейного программирования симплексным методом:
1. Привести задачу линейного программирования к каноническому виду.
2. Привести систему ограничений (1) к допустимому виду (4) и найти начальное базисное решение. Если начальное допустимое базисное решение отсутствует, то условия задачи противоречивы и оптимального решения нет.
3. Составить первую симплексную таблицу. Если система ограничений (1) приведена к допустимому виду (3), а целевая функция (2) к виду (5), то первая симплексная таблица примет вид (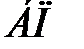 - базисные переменные,
- базисные переменные,  - свободные члены):
- свободные члены):

| 
| 
| 
| 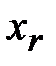
| 
| 
| 
| 
| 
| 
|

| 
| 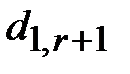
| 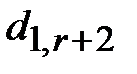
| 
| 
| 
| ||||

| 
| 
| 
| 
| 
| 
| ||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
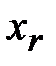
| 
| 
| 
| 
| 
| 
| ||||

| 
| 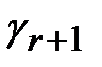
| 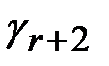
| 
| 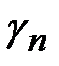
| 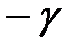
| - |
4. Предположим, что целевая функция (5) стремится к максимуму. Если задача линейного программирования на минимум  , то ее можно свести к задаче на максимум путем умножения целевой функции на
, то ее можно свести к задаче на максимум путем умножения целевой функции на 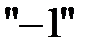 , то есть
, то есть  .В этом случае, если в последней строке первой симплексной таблицы (кроме числа
.В этом случае, если в последней строке первой симплексной таблицы (кроме числа 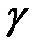 ) все числа отрицательные, то есть все
) все числа отрицательные, то есть все 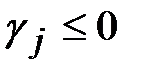 , то базисное решение
, то базисное решение  является оптимальным и
является оптимальным и  .
.
5. Пусть среди чисел  имеется хотя бы одно положительное число, причем наибольшее из этих чисел находится в столбце
имеется хотя бы одно положительное число, причем наибольшее из этих чисел находится в столбце  , то есть это
, то есть это  и пусть среди чисел этого столбца есть положительные числа. Для каждого такого числа
и пусть среди чисел этого столбца есть положительные числа. Для каждого такого числа  составляем отношение
составляем отношение  . Из всех таких выражений выбираем наименьшее. Пусть оно соответствует
. Из всех таких выражений выбираем наименьшее. Пусть оно соответствует  строке (базисному неизвестному
строке (базисному неизвестному  ), тогда
), тогда  - строка и
- строка и  - столбец – это разрешающие строка и столбец, а элемент
- столбец – это разрешающие строка и столбец, а элемент  - стоящий на их пересечении – разрешающий элемент.
- стоящий на их пересечении – разрешающий элемент.
6. Осуществим переход к новой таблице. Для этого  разрешающую строку делим на
разрешающую строку делим на  , чтобы разрешающий элемент был = 1, а затем в
, чтобы разрешающий элемент был = 1, а затем в  -ом столбце с помощью
-ом столбце с помощью  -ой строки получаем нули, умножая
-ой строки получаем нули, умножая  строку на соответствующие числа и вычитая их из других строк таблицы. При этом старая базисная неизвестная
строку на соответствующие числа и вычитая их из других строк таблицы. При этом старая базисная неизвестная  станет свободной и заменится на новое базисное неизвестное
станет свободной и заменится на новое базисное неизвестное 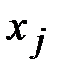 . В результате будет осуществлен переход к новому базису
. В результате будет осуществлен переход к новому базису  .
.
7. С новой таблицей возвращаемся к выполнению пункта 4.
Пример 7. Решить симплексным методом задачу линейного программирования:
 ,
, 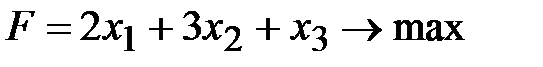 (**),
(**), 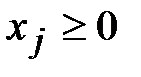 ,
,  .
.
Решение.
1. Приведем задачу к каноническому виду. Для этого введем балансовые переменные: 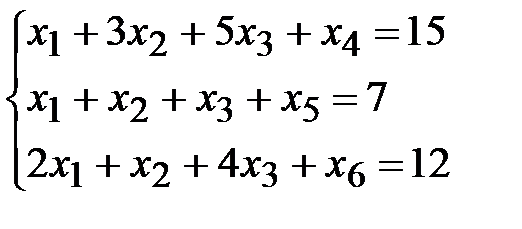 (*).
(*).
2. Так как балансовые переменные введены с положительным знаком (знаки балансовых переменных совпадают со знаками свободных членов), то они могут быть выбраны в качестве базисных. То есть 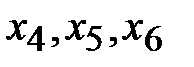 - базисные переменные,
- базисные переменные, 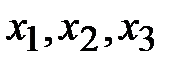 - свободные. Выразим базисные переменные через свободные:
- свободные. Выразим базисные переменные через свободные:  . Отсюда
. Отсюда  - начальное допустимое базисное решение. Целевая функция
- начальное допустимое базисное решение. Целевая функция  не зависит от базисных переменных, то есть уже выражена через свободные, следовательно
не зависит от базисных переменных, то есть уже выражена через свободные, следовательно  - значение функции в начальном решении.
- значение функции в начальном решении.
3. Составим начальную симплексную таблицу используя систему (*) и целевую функцию (**).

| 
| 
| 
| 
| 
| 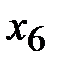
| 
| 
|

| 
| |||||||

| 
| |||||||

| 
| |||||||

| min |
Решение  не является оптимальным, так как в последней строке есть положительные числа. Максимальное из них равно
не является оптимальным, так как в последней строке есть положительные числа. Максимальное из них равно  и соответствует столбцу
и соответствует столбцу  (разрешающий столбец). Для каждого положительного числа столбца
(разрешающий столбец). Для каждого положительного числа столбца  найдем оценку
найдем оценку  и внесем эти оценки в последний столбец первой симплексной таблицы. Среди оценок
и внесем эти оценки в последний столбец первой симплексной таблицы. Среди оценок  выберем минимальную, то есть
выберем минимальную, то есть  . Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть
. Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть  - разрешающий.
- разрешающий.
4. Осуществим переход ко второй симплексной таблице.
Для этого разрешающую (первую) строку разделим на  , чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная
, чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная  станет свободной, а
станет свободной, а  - базисной. Для этого первую строку (после деления на
- базисной. Для этого первую строку (после деления на  ): вычтем из второй строки (
): вычтем из второй строки (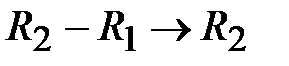 ),вычтем из третьей строки (
),вычтем из третьей строки ( ), умножим на
), умножим на  и вычтем из четвертой строки (
и вычтем из четвертой строки ( ).
).

| 
| 
| 
| 
| 
| 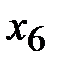
| 
| 
|
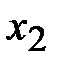
| 1/3 | 5/3 | 1/3 | 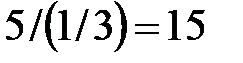
| ||||

| 2/3 | -2/3 | -1/3 | 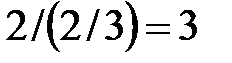
| ||||

| 5/3 | 7/3 | -1/3 | 
| ||||

| -4 | -1 | -15 | min |
Решение 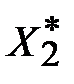 не является оптимальным, так как в последней строке есть положительное число
не является оптимальным, так как в последней строке есть положительное число 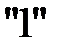 , соответствующее столбцу
, соответствующее столбцу 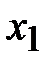 (разрешающий столбец). Для каждого положительного числа столбца
(разрешающий столбец). Для каждого положительного числа столбца  найдем оценку
найдем оценку  и внесем эти оценки в последний столбец второй симплексной таблицы. Среди оценок
и внесем эти оценки в последний столбец второй симплексной таблицы. Среди оценок  выберем минимальную, то есть
выберем минимальную, то есть 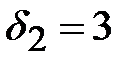 . Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть
. Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть  - разрешающий.
- разрешающий.
5. Осуществим переход к третьей симплексной таблице.
Для этого разрешающую (вторую) строку разделим на  , чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная
, чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная 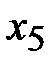 станет свободной, а
станет свободной, а  - базисной. Для этого вторую строку (после деления на
- базисной. Для этого вторую строку (после деления на  ): умножим на
): умножим на  и вычтем из первой строки (
и вычтем из первой строки ( ); умножим на
); умножим на  и вычтем из третьей строки (
и вычтем из третьей строки ( ); вычтем из четвертой строки (
); вычтем из четвертой строки ( ).
).

| 
| 
| 
| 
| 
| 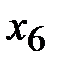
| 
| 
|
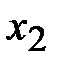
| 1/2 | -1/2 | ||||||
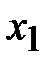
| -1 | -1/2 | 3/2 | |||||

| 1/2 | -5/2 | ||||||

| -3 | -1/2 | -3/2 | -18 | min |
Так как в последней строке нет положительных чисел, то из третьей симплексной таблицы 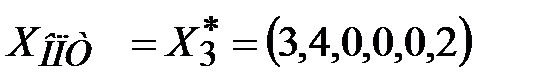 - оптимальное решение,
- оптимальное решение, 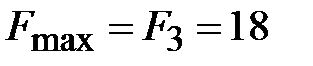 .
.
Задания для решения в аудитории
1. Решить симплексным методом задачу линейного программирования:  ,
, 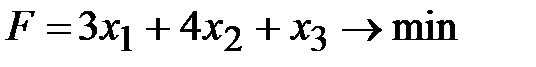 ,
, 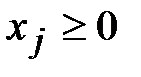 ,
,  .
.
При решении задач линейного программирования симплексным методом могут встретиться особые случаи:
1. Если целевая функция на максимум (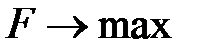 ), в последней строке симплексной таблицы нет положительных чисел, но при этом хотя бы одно из чисел последней строки стоящее в столбце для свободной переменной, равно нулю, то задача имеет бесконечное множество решений.
), в последней строке симплексной таблицы нет положительных чисел, но при этом хотя бы одно из чисел последней строки стоящее в столбце для свободной переменной, равно нулю, то задача имеет бесконечное множество решений.
2. Если целевая функция на максимум ( ), в последней строке есть хотя бы одно положительное число, но в столбце, соответствующем этому числу, положительных чисел нет, то задача не имеет оптимального решения (
), в последней строке есть хотя бы одно положительное число, но в столбце, соответствующем этому числу, положительных чисел нет, то задача не имеет оптимального решения ( )
)
Пример 8. Решить симплексным методом задачу линейного программирования:
 ,
,  (**),
(**), 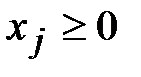 ,
,  .
.
Решение.
1. Приведем задачу к каноническому виду. Для этого введем балансовые переменные:  (*).
(*).
2. Так как балансовые переменные введены с положительным знаком (знаки балансовых переменных совпадают со знаками свободных членов), то они могут быть выбраны в качестве базисных. То есть 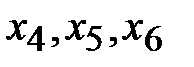 - базисные переменные,
- базисные переменные, 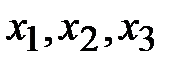 - свободные. Выразим базисные переменные через свободные:
- свободные. Выразим базисные переменные через свободные:  . Отсюда
. Отсюда 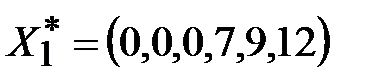 - начальное допустимое базисное решение. Целевая функция
- начальное допустимое базисное решение. Целевая функция  не зависит от базисных переменных, то есть уже выражена через свободные, следовательно
не зависит от базисных переменных, то есть уже выражена через свободные, следовательно  - значение функции в начальном решении.
- значение функции в начальном решении.
3. Составим начальную симплексную таблицу используя систему (*) и целевую функцию (**).

| 
| 
| 
| 
| 
| 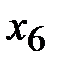
| 
| 
|

| 
| |||||||

| 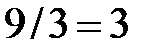
| |||||||

| 
| |||||||

| min |
Решение  не является оптимальным, так как в последней строке есть положительные числа. Все числа одинаковые, выберем любое, например число
не является оптимальным, так как в последней строке есть положительные числа. Все числа одинаковые, выберем любое, например число 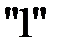 в столбце
в столбце  (разрешающий столбец). Для каждого положительного числа столбца
(разрешающий столбец). Для каждого положительного числа столбца  найдем оценку
найдем оценку  и внесем эти оценки в последний столбец первой симплексной таблицы. Среди оценок
и внесем эти оценки в последний столбец первой симплексной таблицы. Среди оценок  выберем минимальную. Таких оценок две, выберем любую, например
выберем минимальную. Таких оценок две, выберем любую, например 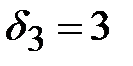 . Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть
. Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть  - разрешающий.
- разрешающий.
4. Осуществим переход ко второй симплексной таблице.
Для этого разрешающую (третью) строку разделим на 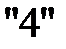 , чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная
, чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная  станет свободной, а
станет свободной, а  - базисной. Для этого третью строку (после деления на
- базисной. Для этого третью строку (после деления на  ): вычтем из первой строки (
): вычтем из первой строки (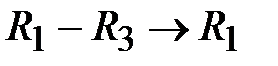 ); умножим на
); умножим на  и вычтем из второй строки (
и вычтем из второй строки (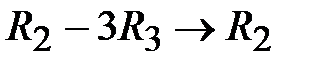 ); вычтем из четвертой строки (
); вычтем из четвертой строки ( ).
).

| 
| 
| 
| 
| 
| 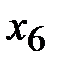
| 
| 
|
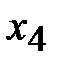
| 1/4 | 3/4 | -1/4 | 
| ||||
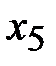
| -1/4 | 1/4 | -3/4 | 
| ||||

| 3/4 | 1/4 | 1/4 | 
| ||||

| 1/4 | 3/4 | -1/4 | -3 | min |
Решение  не является оптимальным, так как в последней строке есть положительные числа. Выберем максимальное из них
не является оптимальным, так как в последней строке есть положительные числа. Выберем максимальное из них  , соответствующее столбцу
, соответствующее столбцу  (разрешающий столбец). Для каждого положительного числа столбца
(разрешающий столбец). Для каждого положительного числа столбца  найдем оценку
найдем оценку 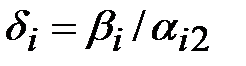 и внесем эти оценки в последний столбец второй симплексной таблицы. Среди оценок
и внесем эти оценки в последний столбец второй симплексной таблицы. Среди оценок  выберем минимальную, то есть
выберем минимальную, то есть  . Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть
. Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть  - разрешающий.
- разрешающий.
5. Осуществим переход к третьей симплексной таблице.
Для этого разрешающую (вторую) строку разделим на  , чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная
, чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная 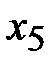 станет свободной, а
станет свободной, а  - базисной. Для этого вторую строку (после деления на
- базисной. Для этого вторую строку (после деления на  ): умножим на
): умножим на 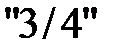 и вычтем из первой строки (
и вычтем из первой строки (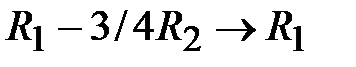 ); умножим на
); умножим на  и вычтем из третьей строки (
и вычтем из третьей строки (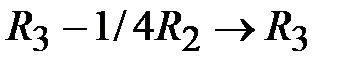 ); умножим на
); умножим на  и вычтем из четвертой строки (
и вычтем из четвертой строки ( ).
).

| 
| 
| 
| 
| 
| 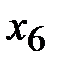
| 
| 
|

| -3 | 
| ||||||

| -1 | -3 | - | |||||
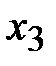
| -1 | 
| ||||||

| -3 | -3 | min |
Решение  не является оптимальным, так как в последней строке есть положительные числа. Выберем максимальное из них
не является оптимальным, так как в последней строке есть положительные числа. Выберем максимальное из них 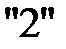 , соответствующее столбцу
, соответствующее столбцу  (разрешающий столбец). Для каждого положительного числа столбца
(разрешающий столбец). Для каждого положительного числа столбца  найдем оценку
найдем оценку  и внесем эти оценки в последний столбец второй симплексной таблицы. Среди оценок
и внесем эти оценки в последний столбец второй симплексной таблицы. Среди оценок  выберем минимальную, то есть
выберем минимальную, то есть 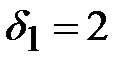 . Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть
. Строка соответствующая минимальной оценке будет разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки является разрешающим, то есть  - разрешающий.
- разрешающий.
6. Осуществим переход к четвертой симплексной таблице.
Для этого разрешающую (первую) строку разделим на  , чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная
, чтобы разрешающий элемент был равен 1. Затем в разрешающем столбце необходимо получить все нули, кроме разрешающего элемента. При этом базисная переменная  станет свободной, а
станет свободной, а  - базисной. Для этого первую строку (после деления на
- базисной. Для этого первую строку (после деления на  ): умножим на
): умножим на 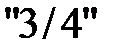 и вычтем из второй строки (
и вычтем из второй строки ( ); вычтем из третьей строки (
); вычтем из третьей строки (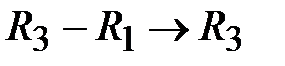 ); умножим на
); умножим на  и вычтем из четвертой строки (
и вычтем из четвертой строки ( ).
).

| 
| 
| 
| 
| 
| 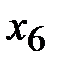
| 
| 
|
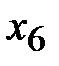
| 1/2 | 1/2 | -3/2 | |||||

| 1/2 | 3/2 | -1/2 | |||||
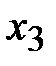
| 1/2 | -1/2 | 1/2 | |||||

| -1 | -7 | min |
В последней строке симплексной таблицы нет положительных чисел, но при этом есть числа стоящие в столбцах для свободных переменных, равные нулю (при  и
и  ). Следовательно, максимальное значение функции
). Следовательно, максимальное значение функции 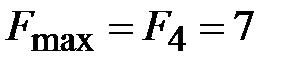 . Это значение может быть достигнуто на бесконечном множестве решений. Одним из решений этого множества является
. Это значение может быть достигнуто на бесконечном множестве решений. Одним из решений этого множества является  . Для того чтобы найти следующее решение перейдем к пятой симплексной таблице.
. Для того чтобы найти следующее решение перейдем к пятой симплексной таблице.
7. В последней строке нет положительных элементов. Выберем столбец соответствующий свободной переменной и содержащий ноль в последней строке, например столбец 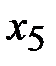 . Среди элементов этого столбца имеется только один положительный
. Среди элементов этого столбца имеется только один положительный  . Выберем его в качестве разрешающего. Далее третью строку разделим на
. Выберем его в качестве разрешающего. Далее третью строку разделим на 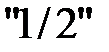 , чтобы разрешающий элемент был равен
, чтобы разрешающий элемент был равен  . После деления на
. После деления на 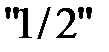 третью строку прибавим к первой и ко второй. При этом базисная переменная
третью строку прибавим к первой и ко второй. При этом базисная переменная  станет свободной, а
станет свободной, а  - базисной.
- базисной.

| 
| 
| 
| 
| 
| 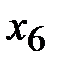
| 
| 
|
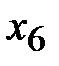
| -1 | -2 | ||||||

| -1 | -1 | ||||||

| -1 | |||||||

| -1 | -7 | min |
Получено новое решение  . При этом выполненные преобразования не повлияли на значение целевой функции:
. При этом выполненные преобразования не повлияли на значение целевой функции:  . Таким образом улучшить целевую функцию нельзя, она достигла возможного максимума.
. Таким образом улучшить целевую функцию нельзя, она достигла возможного максимума.
Дальнейшие преобразования симплексных таблиц можно выполнять бесконечно, при этом будут получаться различные оптимальные решения.
Задания для решения в аудитории
1. Решить симплексным методом задачу линейного программирования:  ,
, 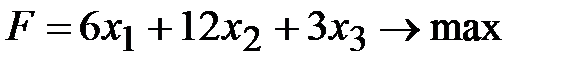 ,
, 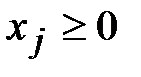 ,
,  .
.
2. Решить симплексным методом задачу линейного программирования: 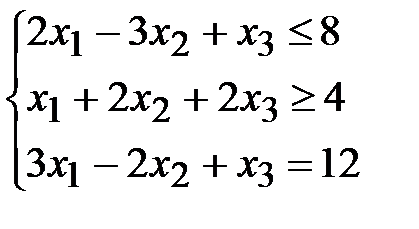 ,
,  ,
, 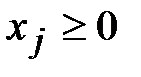 ,
,  .
.
Задания для самостоятельной подготовки
Решить задачи линейного программирования симплексным методом 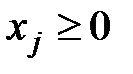 ,
, 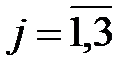 :
:
1) 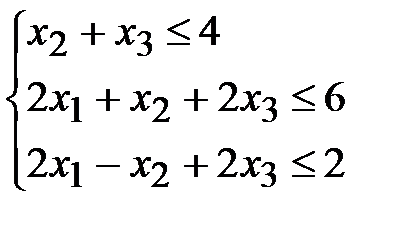 2)
2)  3)
3) 
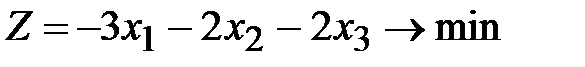


Ответы: 1. 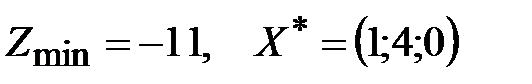 . 2.
. 2.  ,
,  ,
,  . 3. Оптимального решения нет,
. 3. Оптимального решения нет,  .
.
|
|
Дата добавления: 2015-06-27; Просмотров: 960; Нарушение авторских прав?; Мы поможем в написании вашей работы!