Алгоритм проверки формул на логическое следование

Санитарно-гигиенические показатели.

Химические показатели.

Вода характеризуется ионным составом:

- натрий, калий;

- хлориды, сульфаты;

- карбонаты, бикарбонаты (они все вместе обусловливают щелочность воды);

- кальций, магний (влияют на жесткость воды);

- железо и марганец (в зависимости от рН могут находиться либо в окислительной, либо в восстановительной форме в виде комплексов, коллоидов, дисперсных частиц);

- силикаты могут присутствовать в органических и неорганических формах;

- фтор, необходимый в биологическом питании для предотвращения таких заболеваний, как кариес и флюороз, в концентрации 0,7 – 1,5 мг / л, содержится в виде аниона;

- азотсодержащие вещества (ионы аммония, нитриты и нитраты), внесенные с бытовыми, промышленными и дренажными сточными водами и кислотными дождями.

Токсические вещества (стронций, свинец, ртуть, бериллий и др.), а также радионуклиды.

В основном это антропогенные продукты. Растворенные в воде газы – кислород, углекислый газ, сероводород, метан, аммиак (обусловливают запахи и коррозионную активность воды по отношению к трубопроводам и оборудованию).

В настоящее время существуют две главных проблемы водных ресурсов:

1) уменьшаются запасы пресной воды, пригодной для хозяйственно-питьевых нужд, по причинам нерационального их использования и загрязнения;

2) происходит загрязнение Мирового океана нефтепродуктами и отходами других производств.

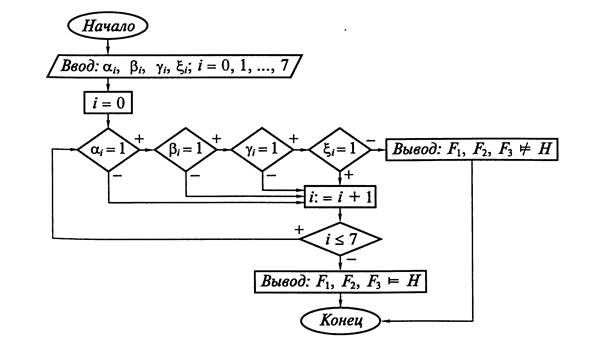
Алгоритм действует следующим образом. Он просматривает последовательно по строкам таблицы значений формул F1, F2, F3, H. Если хотя бы один элемент нулевой строки α₀, β₀, γ₀ равен 0, то без просмотра значения формулы H в этой строке (т. е. числа ξ₀) происходит переход к просмотру следующей строки α₁, β₁, γ₁. Если все элементы α₀, β₀, γ₀ нулевой строки равны 1, то просматривается значение ξ₀ формулы H в этой строке. При ξ₀ = 0 выдается результат: формула H не является логическим следствием формул F1, F2, F3. При ξ₀ = 1 происходит переход к просмотру следующей строки α₁, β₁, γ₁. И так далее. Если после просмотра последней строки α₇, β₇, γ₇, ξ₇ должен произойти переход к просмотру следующей строки, то это означает, что определение логического следования выполнено и формула H является логическим следствием формул F1, F2, F3.

Пример 1. По таблице истинности нескольких формул попытаемся определить, какие из них следуют из каких:

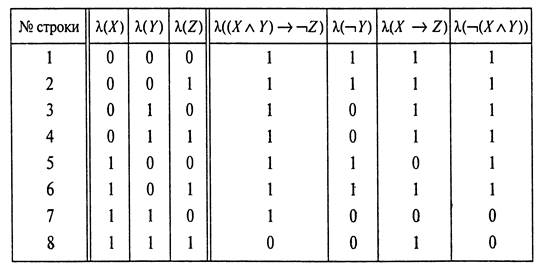
Рассмотрим формулы Х, Z, (X _^ Y) → Z, Y. Из таблицы видно, что имеется только одна строка (6-я), в которой первые три формулы принимают значение 1. В этой строке и формула Y также принимает значение 1. Следовательно, X, Z, (X _^ Y) → Z ╞ Y

Теперь рассматриваем формулы (Х _^ Y) → Z, Х → Z, (Х _^ Y). Из таблицы видно, что имеется точно пять строк, в которых первые две формулы принимают значение 1, а именно 1-я, 2-я, 3-я, 4-я и 6-я. В этих строках третья формула также принимает значение 1. Следовательно, (X _^ Y) → Z, X → Z ╞ (Х _^ Y).

Признаки логического следствия.

То, что некоторая формула является логическим следствием каких-то формул, можно выразить так же, сказав, что подходящая формула является тавтологией. В этом существо признаков, о которых пойдет речь в настоящем пункте, чем еще раз подчеркивается важное значение тавтологий.

Теорема 6.3 (признак логического следствия). Формула Н будет логическим следствием формулы F тогда и только тогда, когда формула F → Н является тавтологией: F ╞ H ↔ ╞ F → H.

Доказательство. Необходимость. Дано: F (X₁,..., Х_n) ╞ Н (X₁,..., Х_n), т.е. если для набора высказываний А₁,..., А_n имеет место λ(F (А₁,..., А_n)) = 1, то λ(H (А₁,..., А_n)) = 1. Тогда для любого набора высказываний А₁,..., А_n имеет место равенство λ(F (А₁,..., А_n)) → λ(H (А₁,..., А_n)) = 1, поскольку равенство нулю возможно лишь в том случае, когда λ(F (А₁,..., А_n)) = 1 и λ(H (А₁,..., А_n)) = 0, но такая ситуация исключена условием. Следовательно, на основании равенства (1.4) λ(F (А₁,..., А_n)) → λ(H (А₁,..., А_n)) = 1 для любых высказываний А₁,..., А_n. Это означает, что формула F (X₁,..., Х_n) → Н (X₁,..., Х_n) — тавтология, т.е. ╞ F → Н.

Достаточность. Дано: ╞ F → Н. Тогда: λ(F (А₁,..., А_n)) → λ(H (А₁,..., А_n)) = 1 для любых высказываний А₁,..., А_n, откуда в силу равенства (1.4) λ(F (А₁,..., А_n)) → λ(H (А₁,..., А_n)) = 1. Предположим теперь, что λ(F (А₁,..., А_n)) = 1. Тогда: 1 → λ(H (А₁,..., А_n)) = 1, откуда (на основании определения 1.7) λ(H (А₁,..., А_n)) = 1, ибо в противном случае 1 → 0 = 1 — противоречие. Но это значит (по определению 6.1 логического следствия), что F ╞ H.

Следующая теорема дает признаки того, что формула является логическим следствием двух или большего количества формул.

Теорема 6.4. Для любых формул F₁, F₂,..., F_m,╞ H (m ≥ 2) следующие утверждения равносильны:

а) F₁, F₂,..., F_m ╞ H;

б) F_{1 ^} F_{2 ^}... _^ F_m ╞ H;

в) ╞ (F_{1 ^} F_{2 ^}... _^ F_m) → H.

Доказательство. Утверждения б) и в) равносильны на основании предыдущей теоремы. Докажем равносильность утверждений а) и б).

а) => б). Дано: F₁, F₂,..., F_m ╞ H Покажем, что F_{1 ^} F_{2 ^}... _^ F_m ╞ H. Пусть A₁, …, A_n — такие конкретные высказывания, что

λ(F₁ (A₁, …, A_n) _^ … _^ F_m (A₁, …, A_n)) = 1

Тогда по равенству (1.2)

λ(F₁ (A₁, …, A_n)) _^ … _{^ λ(} F_m (A₁, …, A_n)) = 1

Отсюда по определению 1.3

λ(F₁ (A₁, …, A_n)) = 1, …, _λ( F_m (A₁, …, A_n)) = 1

Но поскольку по условию F₁, F₂,..., F_m ╞ H, то отсюда следует, что λ(H (A₁, …, A_n)) = 1. Следовательно, F_{1 ^} F_{2 ^}... _^ F_m ╞ H.

б) => а). Дано: F_{1 ^} F_{2 ^}... _^ F_m ╞ H. Покажем, что F₁, F₂,..., F_m ╞ H. Предположим, что справедливы все соотношения (6.3) для некоторых A₁, …, A_n. Тогда имеет место соотношение (6.2), из которого на основании равенства (1.2) приходим к соотношению (6.1). Из последнего на основании условия F_{1 ^} F_{2 ^}... _^ F_m ╞ H заключаем: λ(H (A₁, …, A_n)) = 1. Но это и означает, что F₁, F₂,..., F_m ╞ H.

Два свойства логического следования.

Свойства, формулируемые в теореме 6.5, используются для доказательства того, что какая-то формула является логическим следствием некоторых формул (см. пример 6.2).

Теорема 6.5. Отношение логического следования между формулами алгебры высказываний обладает следующими свойствами:

а) F1, Ръ..., Fm *= Fh для / = 1, 2,..., т\

б) если Fu F2,..., Fm *= Gjjumj = 1, 2,..., p и Gh G2,..., Gp t= H,

то Fu F2,..., Fm i= Я.

Доказательство. а) Фактически это свойство состоит в следующем: F/ •= Fh Оно непосредственно вытекает из определения 6.1 логического следования и означает, что отношение логического следования рефлексивно.

б) В частном случае при т-р-\ данное свойство утверждает: если F i= G и G»= Я, то F»= Я. Другими словами, отношение логического следования транзитивно. Докажем исходное утверждение. Строим таблицу истинности для всех формул, указанных в утверждении б), перечислив все пропозициональные переменные Хь Х2,..., Хт входящие хотя бы в одну из этих формул. Рассмотрим какую-нибудь строку этой таблицы, в которой каждая формула Fb F2,..., Fm получает истинностное значение, равное 1. Тогда на основании условий каждая из формул Gu G2,..., Gp также принимает истинностное значение, равное 1. Следовательно, и Я имеет значение 1. Таким образом, для всякого набора истинностных значений переменных Хи Хъ..., Хп, для которого каждая формула Fu F2,..., Fm принимает значение 1, формула Я также принимает значение 1. Это означает, что Fu F2,..., Fm t= Я. □

Следование и равносильность формул.

Если говорить о следовании из одной формулы другой, то получаем бинарное отношение на совокупности всех формул алгебры высказываний. Две формулы Fw Я (в указанном порядке) находятся в данном отношении, если F*= Я.

В § 4 рассмотрены бинарные отношения равносильности на совокупности всех формул алгебры высказываний. Две формулы Fw Я (в указанном порядке) находятся в этом отношении, если F = Я. Там же (следствие 4.3) установлено, что отношение равносильности формул есть отношение эквивалентности. Установим взаимосвязь между отношением равносильности и отношением следования.

Теорема 6.6. Две формулы алгебры высказываний равносильны тогда и только тогда, когда каждая из них является логическим следствием другой: F=H<^>Ft=HnH*=F.

Доказательство. Необходимость. Дано: F= Я. По определению равносильности обе формулы F(XU..., Хп) и Н(Хи..., Хп) для любых конкретных высказываний Аи..., Ап превращаются в высказывания F(AU..., Ап) и Н(Аи..., Ап), которые одновременно либо оба истинны, либо оба ложны. А раз так, то каждое из высказываний F(AU..., Ап) -* Н(Аи..., Ап) и Н(Аи..., Ап) -» -> F(AU..., Ап) истинно для любых конкретных высказываний А\,..., Ап. Это означает, что t=F->Hnt=H->F, откуда, по теореме 6.3, F t= Я и Я t= F.

Достаточность. Дано: Ft= Ни Н*= F. Тогда, по теореме 6.3, *= F-> -> Ни *= Я-» F. Поскольку формула /*-> Я всегда превращается в истинное высказывание и формула Н -^ F всегда превращается в истинное высказывание, то и их конъюнкция (F -» Я) л (Я -> F) является формулой, которая превращается в истинное высказывание всегда, т.е.»= (F-^> Я) л (Я-> F). Но на основании теоремы 4.4, ч, (F -» Я) л (Я -» i7) = F<-> Я. Тогда по замечанию 4.7 t= i7^-» Я, а по теореме 4.2 F= Я.

Замечание 6.7. Если некоторая формула является тавтологией, то и всякое ее логическое следствие также является тавтологией. Символически это можно записать так: t=FHFt=H=$t=H

Правила логических умозаключений.

Теперь можем рассмотреть примеры структур правильного мышления, т.е. ответить на вопрос, что из чего следует.

Начнем с тавтологии из теоремы 3.1,/с: t= (Fa(F-> G)) -> G. (На основании замечания 3.7 пропозициональные переменные Р и Q заменены произвольными формулами Fn G алгебры высказываний.) На основании теоремы 6.4 заключаем, что F, /*-> G*= G. Полученную схему, или правило вывода (умозаключения), также называют правилом modus ponens.

Правило 6.8 {modus ponens): '.

G

Это правило означает, что от утверждения об истинности посылки F с помощью другой посылки F -» G переходят к утверждению об истинности следствия G. Данное правило называют также правилом заключения или отделения (от посылки F -> G с помощью посылки Fотделяется заключение G). По теореме 3.5 правилу 6.8 можно придать несколько иной смысл: если формулы, стоящие в числителе, являются тавтологиями, то и формула в знаменателе — также тавтология.

Не менее важное и широко применяемое в рассуждениях правило умозаключения получается на основе тавтологии теоремы 3.1, л.

Правило 6.9 (modus tollens): '~*.

—i Г

Оно называется правилом modus tollens: от отрицания истинности посылки G с помощью посылки F -» G переходят к отрицанию истинности F.

Таким образом, рассмотренные правила вывода 6.8 и 6.9 позволяют в истинной импликации F-> Сиз истинности посылки F делать вывод об истинности следствия G, а из ложности следствия G — о ложности посылки F.

Укажем еще некоторые правила вывода, применяемые в рассуждениях. Путь их получения состоит в том, что сначала заменяем в соответствующей тавтологии каждую пропозициональную переменную произвольной формулой алгебры высказываний, в результате чего на основании теоремы 3.6 снова получаем тавтологию, а затем от нее по теореме 6.3 переходим к соответствующему правилу вывода (умозаключения), которое и записываем в принятой форме. Так, тавтология теоремы 3.3, б дает следующее правило вывода:

Правило 6.10 (введения конъюнкции): ' ■

Из тавтологий теоремы 3.2, б приходим к таким правилам вывода:

Правило 6.11 (удаления конъюнкции):

Правило 6.12 (введения дизъюнкции):

F G

F G

FaG9 FaG

Смысл названий этих правил виден из характера их действия.

Из тавтологии теоремы 3.1, д получаем правило контрапозиции.

JT» >Т

Правило 6.13 (контрапозиции): — -.

—\G —> —\F

Из тавтологии теоремы 3.1, е вытекает правило цепного заключения (или правило силлогизма).

жт *и, ч F->

Правило 6.14 (цепного заключения):.

г —> Н

Из тавтологии теоремы 3.1, м следует правило перестановки посылок.

тт tier ч F->(G-*H)

Правило 6.15 (перестановки посылок): -.

G -> (Z1-» H)

Наконец, из тавтологии теоремы 3.1, н получаем следующие правила:

Правила 6.16 (объединения и разъединения посылок):

F->(G-*H) (FaG) ->Я

(F aG)^H ' F^(G-^H)'

Правило 6.17 (расширенной контрапозиции):

(FaG) ->Я

(F л-н#)->-.£'

Аналогично формулируются другие правила вывода тавтологий, что рекомендуется проделать самостоятельно.

На правила 6.8 — 6.17 можно смотреть с двух точек зрения. Во-первых, каждое из них представляет собой утверждение следующего типа: формула, записанная в знаменателе, является логическим следствием всех формул, записанных в числителе данного правила. Во-вторых, каждое из этих правил можно рассматривать как правило получения новой тавтологии из уже имеющихся: если все формулы, записанные в числителе, являются тавтологиями, то тавтологией будет и формула, записанная в знаменателе правила (для доказательства этого утверждения примените замечание 6.7).

Еще один способ проверки логического следования. Требуется выяснить, является ли формула Н(Хи..., Х„) логическим следствием формул FX(XU..., Х„),..., Fm(Xu..., Хп), т.е. Fu Ръ..., Fm *= Я. Предположим, что Яне есть логическое следствие формул Fu F2,..., Fm. Значит, существуют такие конкретные высказывания Аъ..., Ап, что высказывание Н(АЪ..., Ап) ложно, в то время как все высказывания Fx(Ab..., Ап),..., Fm(Au..., Ап) истинны. Если при этом удается найти распределение нулей и единиц между значениями переменных Хь..., Хт соответствующее сделанному предположению, то предположение верно. Если же возникает противоречие, то предположение неверно. Посмотрим на примерах, как это делается.

Пример 6.18. Выясните, выполняется ли логическое следование

*= Xv Z.

Допустим, что существуют такие конкретные высказывания А, В, С, что Х(А -> (-.В v С)) = 1, Х(гА) = 1, ЦВ -> С) = 1, но Х(А v С) = 0. Тогда из последнего соотношения получаем Х(А) = 0, ЦС) = 0, что не противоречит соотношению Ц-Л) = 1. Далее, соотношение Х(В -» С) = 1 дает ЦВ) = 0 (так как ЦС) = 0). Наконец, вычислив при данных значениях А, Ви С значение Х(А -> -»(-ii? v С)), убеждаемся что оно равно 1, а это находится в полном соответствии с допущением. Следовательно, приходим к выводу: если высказывания А, В, С таковы, что Х(А) = Х(В) = ЦС) = 0, то при подстановке X = A, Y= В, Z = С формулы-посылки примут значение 1, а формула Xv Z примет значение 0. Значит, формула Xv Zne выводима из формул X-» (-iKv Z), -лХ, Y-> Z

Нахождение следствий из данных посылок.

Мы научились определять, является ли данная формула логическим следствием некоторых других данных формул. Теперь возникает вопрос, как можно находить все формулы, являющиеся логическим следствием данной совокупности формул. Следующая теорема дает ключ к решению этой задачи.

Теорема 6.19. Формула Н(ХХ,..., Хп), не являющаяся тавтологией, тогда и только тогда будет логическим следствием формул FX(XX,..., Хп),..., Fm(Xx,..., Хп), не все из которых являются тавтологиями, когда все совершенные дизъюнктивные одночлены из разложения формулы Не совершенную конъюнктивную нормальную форму входят в совершенную конъюнктивную нормальную форму формулы ад, -, хп) а... л Fm{xb..., хп).

Доказательство. Необходимость. Дано: Fb..., Fm*= HТогда, по теореме 6.4, Fx л... л Fm *= Н Найдем для формул Fx л... л Fm и Яих совершенные конъюнктивные нормальные формы. Такая форма для каждой не тождественно истинной формулы существует и единственна с точностью до порядка совершенных дизъюнктивных одночленов в конъюнкции (см. теорему 5.5). Пусть Dx л... л Dk — СКН-форма для формулы Fx л... л Fm9 а Нх л... л Я7— СКН-форма для формулы Н Тогда: Fx л... л Fm = Д л... л Dk, Н= Нх л... л Ht.

Допустим, что заключение теоремы не выполняется, т. е. среди совершенных дизъюнктивных одночленов Нъ..., Я/ имеется такой, которого нет среди совершенных дизъюнктивных одночленов Du..., Dk. He нарушая общности (ввиду несущественности порядка вхождения одночленов Яь..., Я/ в СКН-форму Нх л... л Я/), можем считать, что таким одночленом является, например, Нх. Итак, ВД,..., Хп) Z DX(XX,..., Хп),..., НХ(ХЬ..., Хп) 2 Dk(Xx,..., Хп). Тогда существует единственный (с точки зрения логических значений) набор Аи..., Ап, на котором совершенный дизъюнктивный одночлен Нх{Хи..., Хп) принимает значение 0: Х(НХ(АХ,..., Ап)) = 0, откуда

ЦЩАХ,..., Л)) = 0. (1)

Этот набор выбирается следующим образом. Если переменная Х{ входит в Нх без знака отрицания, то А,- таково, что X(Aj) = 0; если X,- входит в Нх со знаком отрицания, то А,- таково, что \(Aj) = 1 (1 < / < п). Каждый из совершенных дизъюнктивных одночленов Du..., Dk в силу его отличия от совершенного дизъюнктивного одночлена Нх обращается на данном наборе в 1 (почему?): UDX(AX,..., Л)) = 1,..., 4Dk(Au..., Л)) = 1. Тогда X(DX(AU..., Ап)) л... л Dk(Ax,..., Ап)) = 1, откуда, в силу равносильности Dx л... л Dk = s F, л... л Fm получаем X(FX(AX,..., Л) а... л Fm(Au..., Л)) = 1. Следовательно, А,(/!(Л,,..., Ап)) л... лЦ/^Ль..., А„)) = 1, а значит,

..., Л)) = 1,.-, M^Wi,..., Ап)) = 1. (2)

Соотношения (1) и (2) противоречат условию: Fx,..., Fm *= Н Следовательно, в СКН-форме формулы Н нет ни одного совершенного дизъюнктивного одночлена, который отсутствовал бы в СКН-форме формулы Fx л... л Fm.

Достаточность. Пусть Dx л... л Dk — СКН-форма формулы Fx л... л Fm. Тогда F\ л... л Fm = Dx л... л Dk. Пусть далее #= Д, л... л /)/5, где 1 < /ь..., is < к и /l5..., /, попарно различны. Тогда ясно, что если при некоторой подстановке формула fl л... л Fm принимает истинное значение, то и равносильная ей формула Dx л... л Dk также принимает значение 1. Следовательно, и все члены Du..., Dk последней конъюнкции принимают значение 1, включая члены Di{9..., Dis. Но тогда и конъюнкция Dix л... л Dis = Н также принимает значение 1. Значит, Fu..., Fm»= Я. П

Эта теорема определяет следующее правило (алгоритм) для нахождения всех (неравносильных) формул, являющихся логическими следствиями из посылок Fl9..., Fm: 1) составить конъюнкцию Fx л... л Tv,; 2) найти СКН-форму формулы Fx л... л Fm\ Ъ) выписать все совершенные дизъюнктивные одночлены найденной СКН-формы, а также всевозможные конъюнкции этих одночленов. Полученное множество формул и является искомым (см. Задачник, № 2.34, л).

Нахождение посылок для данного следствия.

Задача нахождения всех формул, из которых данная формула логически следует, является обратной по отношению к той, которая была рассмотрена в предыдущем пункте. Ее решение основывается на следующей теореме.

Теорема 6.20. Чтобы найти все формулы, логическим следствием каждой из которых будет данная формула G(XX,..., Хп), нужно действовать по следующему алгоритму. Найти СКН-форму для формулы G(XU...,Хп); выявить все совершенные дизъюнктивные одночлены, которые в ней отсутствуют', составить всевозможные конъюнкции формулы G(Xx,...,Xn) с недостающими дизъюнктивными одночленами. Получившаяся совокупность формул (вместе с формулой G) будет искомой (с точностью до равносильности формул).

Доказательство. Ясно, что из каждой формулы этой совокупности будет логически следовать формула G, так как G л Н *= G (конъюнкция сильнее каждого из сомножителей). Обратно, покажем, что каждая формула F, из которой логически следует данная формула G, имеет указанный вид, т.е. представляет собой конъюнкцию формулы G и некоторых совершенных дизъюнктивных одночленов, отсутствующих в СКН-форме для G. В самом деле, пусть F *= Си G = Dx л D2 л... л Dk — СКН-форма для формулы G(XX,..., Хп) и F= А! л А2 л... лА,- СКН-форма для формулы F(XU..., Xn). По определению логического следования, F *= G означает, что если формула F(XU..., Хп) на некотором наборе Аи..., Ап значений пропозициональных переменных приняла значение 1, то и формула G(XU..., Хп) на этом наборе примет значение 1. Другими словами, если формула G{XX,..., Хп) на некотором наборе А\,..., Ап значений пропозициональных переменных принимает значение 0, то и формула F(XU..., Хп) на этом наборе принимает значение 0. Но все наборы значений переменных, на которых G принимает значение 0, находятся во взаимно-однозначном соответствии с совершенными дизъюнктивными одночленами D\, D2,..., Dk, образующими СКН-форму для формулы G, т.е. если G(AU..., Ап) = 0, то Dt{Ab..., Ап) = 0 для некоторого 1 <i< к. Следовательно, F(AU..., Ап) = 0 и значит на этом же наборе принимает значение 0 некоторый совершенный дизъюнктивный одночлен А/, входящий в ее СКН-форму. Но тогда этот одночлен совпадает с одночленом Д. Таким образом, каждый совершенный дизъюнктивный одночлен D, из СКН-формы для G входит в СКН-форму для формулы F, т.е. СКН-форма для У7имеет вид: F= D\ л D2 л... л Dk л A^+1 л... л А5, где A^+1,..., А^ — совершенные дизъюнктивные одночлены от переменных Хи..., Хп, не входящие в СКН-форму для формулы G. П

Заключение

Список использованной литературы

Дата добавления: 2015-06-27