Интегральная и дифференциальная функции распределения

Лекция № 6

Наиболее общей формой задания распределения случайных величин является интегральная функция распределения. Она определяет вероятность того, что случайная величина x примет значение, которое будет меньше фиксированного действительного числа х_i

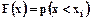. (6.1)

В случае дискретной случайной величины интегральная функция распределения определяется следующим образом

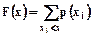. (6.2)

График функции распределения для непрерывной случайной величины имеет вид (рис.6.1):

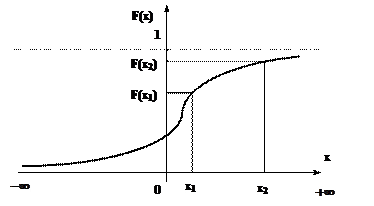
Рисунок 6.1. – Интегральная функция непрерывной случайной величины

Эта функция определена от 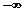до 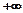. Ее область значений – от 0 до +1. Кривая интегральной функции распределения асимптотически приближается к значению +1.

Вероятность того, что случайная величина x примет значение, меньшее, например, x_1, равна длине отрезка 0x₁ на оси ординат.

Вероятность того, что значение непрерывной случайной величины будет находиться в интервале (x₁, x₂), равна разности значений F(x) в этих точках

.

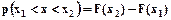На графике (рис.6.1) эта вероятность изображается отрезком на оси ординат соответствующей длины.

Для дискретной случайной величины интегральная функция распределения в соответствии с (6.2) имеет вид ступенчатой ломаной линии (рис.6.2).

Рисунок 6.2 – Интегральная функция распределения дискретной случайной величины

Она скачкообразно возрастает в точках x_i и постоянна в интервалах (x_i,x_i+1),т.к.в самих этих интервалах вероятность того, что х станет меньше x_i, не меняется.

Если F(x) продифференцировать, то получится дифференциальная функция распределения или функция плотности распределения р(х), график которой в случае непрерывной случайной величины имеет вид (рис.6.3):

Рисунок 6.3 – Дифференциальная функция распределения непрерывной случайной величины

Для непрерывных случайных величин область определения р(х) от -∞ до +∞, причем левая и правая ветви графика асимптотически приближаются к оси абсцисс.

Вероятность попадания непрерывной случайной величины х в интервал (х₁, х₂) равна

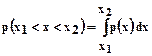(6.3)

Поскольку дифференциальная функция распределения нормирована условием:

,

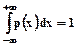то вероятность попадания в интервал (х₁,х₂) интерпретируетсякак относительная доля площади под кривой р(х) (на рис.4.3 она не заштрихована).

Интегральная и дифференциальная функции распределения эквивалентны с точки зрения описания распределений, поскольку все, что можно узнать по F(x), можно узнать и по р(х). Например, вероятность того, что случайная величина х будет меньше фиксированного числа х₁ при помощи дифференциальной функции находится так

.

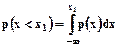Вероятность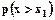

.

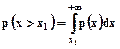Для дискретных случайных величин дифференциальная функция имеет вид ступенчатой линии (рис.6.4):

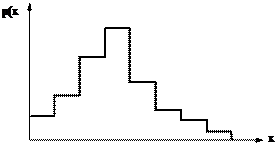Рисунок 6.4 – Дифференциальная функция распределения дискретной случайной величины

Дата добавления: 2014-01-03