Корреляционное отношение

На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.

Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это 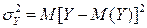. Дисперсию можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим в следующем виде:

. (1.9)

Первое слагаемое обозначим . Это дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака Y);.она измеряет влияние признака X на Y. Второе слагаемое обозначим 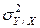. Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией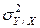измеряет влияние на Y прочих факторов.

Покажем, что действительно можно разложить на два таких слагаемых:

(1.10)

Для простоты полагаем распределение дискретным. Имеем

так как при любом х справедливо равенство

Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии , т.е. рассматривать отношение . Эту величину обозначают 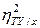и называют теоретическим корреляционным отношением. Таким образом,

(1.11)

Разделив обе части равенства (1.9) на получим

Из последней формулы имеем

(1.12)

Поскольку , так как — составная часть , то из равенства (1.12) следует, что значение 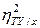всегда заключено между нулем и единицей.

Все сделанные выводы справедливы и для . Из равенства (1.12) следует, что 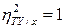только тогда, когда , т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии . В этом случае между Y и X существует функциональная зависимость. Далее, из равенства (1.12) следует, что тогда и только тогда, когда

=M(Y) = const, т.е. линия регрессии Y по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная Y не коррелирована с X (рис. 1.2,а, б, в).

Аналогичными свойствами обладает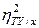— показатель тесноты связи

между X и Y.

Часто используют величину

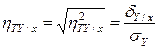. (1.13)

Считают, что она не может быть отрицательной. Значения величины (или ) также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).

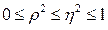Значения , лежащие в интервале 0<<1, являются показателями тесноты группировки точек около кривой регрессии независимо oт её вида (формы связи). Корреляционное отношение связано сследующим образом: . В случае линейной зависимости между переменными . Разность может быть использована как показатель нелинейности связи между переменными.

При вычислении по выборочным данным получаем выборочное корреляционное отношение. Обозначим его. Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид

Дата добавления: 2014-01-03