Математика в Древней Греции

В Древней Греции математика преобразовалась в абстрактную дедуктивную науку.

Характерная черта греческой математики заключается в переходе от одного предложения к другому с помощью доказательства. Так, если раньше решались задачи, как вычислить площадь треугольника или круга, то теперь обсуждается, как доказать результат. В Древней Греции появились первые математические теории.

Из арифметики была выделена в отдельную область теория чисел, наука об общих свойствах операций с натуральными числами. Была разработана теория делимости, рассмотрены арифметические и геометрические прогрессии, отыскивались пифагоровы тройки чисел, удовлетворяющих условию а² + b ² = с².

Одним из главных результатов греческой математики было открытие несоизмеримости. На основе теоремы Пифагора было показано, что диагональ а квадрата со стороной, равной единице, удовлетворяет равенству а² = 1² +1² или а² = 2. Затем, пользуясь теорией делимости, греки доказали, что не существует рационального числа, квадрат которого равен двум. Других чисел, кроме рациональных, в математике еще не было. Таким образом, оказалось, что длина диагонали квадрата со стороной, равной единице, не выражается никаким числом.

Это открытие произвело на греческих ученых огромное впечатление. Поскольку выяснилось, что множество отрезков больше, чем множество чисел, то общую теорию греки строили в геометрической форме. Они разработали правила действий с отрезками.

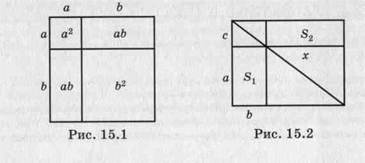
Сложение отрезков давало новый отрезок, получающийся приставлением одного слагаемого отрезка к другому. Результат умножения отрезков а и b понимали как площадь прямоугольника со сторонами а и b. Произведение трех отрезков давало параллелепипед, а произведение большего числа отрезков нельзя было представить. Так была разработана геометрическая алгебра. Например, тождество (а + b)² = а² + 2аb + b² интерпретировалось геометрически, как это показано на рис. 15.1. Решение линейного уравнения ab = сх проводилось с помощью чертежа, подобного рис. 15.2. Легко доказать, что S ₁ = S₂.

Греческие математики нашли общие методы решения квадратных уравнений. Все построения они проводили с помощью циркуля и линейки. Как было показано значительно позже, в XIX в., с помощью циркуля и линейки можно решить только квадратные уравнения и уравнения, сводящиеся к квадратным, например, биквадратные. Поэтому задача удвоения куба, приводящая к кубическому уравнению х³ = 2а³, не могла быть решена средствами геометрической алгебры. Для ее решения был развит метод конических сечений, в математику вошли новые линии — гипербола, эллипс, парабола.

Возможности геометрической алгебры были ограничены также тем, что нельзя было рассмотреть произведение четырех и более величин, и поэтому задачу решения уравнений четвертой степени и выше нельзя было даже поставить.

Открыв несоизмеримость, античные ученые впервые пришли к изучению понятия непрерывности. Заметим, что речь идет о теоретической проблеме. Длину диагонали квадрата можно найти приближенно с любой степенью точности, и вавилонян удовлетворяли приближенные вычисления. На практике инженеры и естествоиспытатели в своих расчетах также пользуются приближенными значениями; так, например, вместо 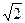обычно берется его приближение. Но для теоретической математики греков важно было точное знание, необходимо было понять «диагональ в самой своей сущности» (выражение Платона), а не приближенное значение. Подчеркнем, что идеально точное измерение величин представляет собой абстракцию. Не имеет смысла уточнять длину линейки за пределы атомных масштабов. Вывод о несоизмеримости диагонали квадрата со стороной вытекает из теоремы Пифагора. Этот теоретический вывод получен с помощью логических рассуждений.

Открыв несоизмеримость, греки впервые встретились с противоположностью дискретного и непрерывного. Изучение дискретных предметов привело науку к понятию целого числа. При изучении линии на первый план выступает понятие непрерывности. Противоречия, связанные с непрерывностью и движением, были вскрыты греческими философами. Особенно известны парадоксы Зенона Элейского. Приведем один из них.

ДИХОТОМИЯ (от греч. — разделяю на две части). «нет движения, потому что то, что движется, должно дойти до середины раньше, чем оно дойдет до конца». Если считать, что точка должна пройти отрезок, равный 1, то, согласно приведенным рассуждениям, она должна пройти сначала 1/2, затем 1/4 и т. д. Получаем бесконечный ряд 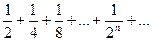, частичная сумма которого равна 1-1/2ⁿ и, следовательно, с ростом п неограниченно приближается к 1. Таким образом, суммирование геометрической прогрессии проводилось уже в Древней Греции.

Выяснение существа непрерывности являлось одной из центральных проблем в античной науке. Эта проблема была тесно связана с вопросом о строении материи, который в то время обсуждался. В греческой науке противостояли друг другу различные тенденции: считать материю безгранично делимой, считать ее состоящей из неделимых частиц, не имеющих протяженности, считать ее состоящей из мельчайших неделимых, но тем не менее протяженных частиц.

Первые математические теории побудили ученых систематизировать отдельные факты и изложить последовательно основы математики. В IIIв. до н. э. были написаны «Начала» Евклида — сочинение, логическая строгость которого получила всеобщее признание. Подробно на семинарах.

«Начала» состоят из 13 книг. В них излагаются основы арифметики, планиметрии и стереометрии. В арифметике исходным понятием была единица. Число определялось как множество, составленное из единиц. Иначе была построена геометрия.

Почему ученые античности не сделали точку единственным исходным понятием геометрии и не рассматривали линию как множество, составленное из точек, а плоскость как множество, составленное из линий? Вопрос о том, состоит ли линия из точек, являлся предметом дискуссии. При определении линии как множества точек сразу же выступали противоречия, связанные с непрерывностью и движением. Именно поэтому ученые древности ввели в геометрию три исходных понятия: точку, прямую, плоскость и сформулировали аксиомы и постулаты, т.е. правила, по которым следует оперировать с введенными понятиями. Таким образом, в «Началах» Евклида геометрия построена аксиоматически.

В первой книге содержатся определения, постулаты и аксиомы. Определения — это пояснения, с помощью которых вводится понятие. Например, «точка есть то, что не имеет частей». Аксиомы у Евклида — это предложения об отношениях равенства и неравенства величин. В «Началах» содержится пять аксиом и пять постулатов.

Дата добавления: 2014-01-03