ЛНДУ 2 – ого порядка с постоянными коэффициентами

ЛОДУ 2 – ого порядка с постоянными коэффициентами.

y’’ + p y’ + q y = 0 (16)

Частные решения ищем в виде y = exp(k x), где k - const, и получаем

exp(k x) (k² + p k + q) = 0. Характеристическое уравнение k² + p k + q = 0

имеет корни k₁, k₂, которые дают два частных решения: y₁ =exp(k₁x), y₂ =exp(k₂x)

и от них переходим к общему решению. Возможны три случая:

1) k₁ 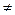k₂, тогда y₀ = C₁ exp(k₁ x) + C₂ exp(k₂ x)

2) k₁ = k₂ = k = -p/2, тогда y₀ = exp(k x) [C₁ + C₂ x ] (17)

3) k₁ = a + i b, тогда y₀ = exp(a x) [C₁ cos bx + C₂ sin bx ]

k₂ = a - i b

Проверка независимости решений. 1) y₁ / y₂ = const;

2) y₂ = x e^-px/2, y`<sub>2</sub> = (1 – px/2) e<sup>-px/2</sup>, y``<sub>2</sub> = (-p + (p/2)<sup>2</sup>x) e<sup>-px/2</sup>, y``<sub>2</sub> + p y`₂ + (p/2)² y₂ =

= [(-p + (p/2)²x) + p (1 – px/2) + (p/2)²x ] e^-px/2 = 0 Þ 0 = 0, y₁ / y₂ = 1/x ¹ const;

3) y₁, y₂ -реальная и мнимая часть функции y = e^{(a ± i b) x}, y₁ / y₂ = ctg bx ¹ const

y’’ + p y’ + q y = f(x) (18)

Методы поиска частного решения неоднородного уравнения:

а) Метод неопределенных коэффициентов

Используется в случае, если f(x) включает e^ax, полином P_n(x) = a₀ xⁿ + a₁x^{n – 1} +.. + a_n,

sin bx, cos bx или их комбинации f(x) = e^ax [ P_n(x) cos bx + Q_m(x) sin bx ], где m, b – постоянные, P_n(x),Q_m(x) -многочлены степени n, m. Частное решение уравнения ищем в таком же виде y*(x) = e^ax [ P _l (x) cos bx + Q _l (x) sin bx ] и перед каждым слагаемым вводим произвольный коэффициент. Здесь l = n m или l = m n. Вполиномахзаписываются все степени х. В некоторых случаях y*(x) дополнительно умножается на x^r

Если f(x) = P_n(x), то y*(x) = x^r (Axⁿ + Bx^{n – 1} +...+ T), где r =

Если f(x) = P_n(x)e^ax, то y*(x) = x^r (Axⁿ + Bx^{n – 1} +...+ T)e^ax, где r = (19)

Если f(x) = (Mcos bx + Nsin bx) e^ax, то y*(x) = x^r(Acos bx + Bsinbx)e^ax, где r =

Подстановка такого решения в неоднородное уравнение приводит к системе линейных уравнений для этих коэффициентов. Решение этой системы окончательно определяет вид частного решения y*(x).

Пр. y`` - 6y` + 9y = e^3x

а) Характеристическое уравнение k² - 6k + 9 = (k – 3)² = 0 имеет один корень k₁ = k₂ = 3. Тогда общее решение однородного уравнения принимает вид y₀ = C₁ e^3x + C₂ x e^3x.

б) Т. к. k₁ = k₂ = а = 3, то частное решение неоднородного ур - я ищем в виде y* = A x² e^3x

y = A x² e^3x | 9

y` = A e^3x (2x + 3x²) | -6

y``= A e^3x (2 + 12x + 9x²) | 1

y`` - 6 y` + 9 = 2A e^3x = e^3x Þ A = ½

Общее решение исходного уравнения y = y₀ + y* = C₁ e^3x + C₂ x e^3x + ½ x² e^3x.

Пр. y’’ + 2y’ – 3y = sin x.

а) Характеристическое уравнение k² + 2k – 3 = 0 имеет корни k₁ = 1, k₂ = -3. Тогда общее решение однородного уравнения y₀ = C₁e^x + C₂e^-3x.

б) Частное решение неоднородного уравнения ищем в виде y* = A sin x + B cos x, тогда

y = Asin x + B cos x | -3

y’ = Acos x - B sin x | 2

y’’ = -Asin x - B cos x | 1

y’’ + 2y’ – 3y = -(4A+2B)sin x + (2A-4B)cos x = sin x получаем 2 условия на

коэффициенты:- 4A – 2B = 1 и 2A – 4B = 0, откуда A = - 1/10, B = - 1/5.

Общее решение исходного уравнения y = y₀ + y* = C₁e^x + C₂e^-3x – 0.1sin x – 0.2cos x.

б) Метод вариации произвольных постоянных

Предлагается частное решение неоднородного уравнения y* искать в виде общего решения однородного уравнения y₀ = A y₁(x) + By₂(x), где A и B уже не константы, а две произвольные функции от х. После такой замены в левой части уравнения имеем 14 слагаемых, которые можно представить в виде (A’y₁ + B’y₂)’ + +p(A’y₁ + B’y₂) + A’y₁’ + B’y₂’ = f(x). Переходот одной неизвестной y* к двум А(х) и В(х) позволяет накладывать на них дополнительное условие. Пусть (A’y₁ + B’y₂) = 0, тогда уравнение существенно упрощается и приходим к системе двух линейных уравнений

A’y₁ + B’y₂ = 0 (20)

A’y’₁ + B’y’₂ = f(x)

Из решения системы находим A’, B’. Интегрируем их и получаемявный вид искомых функций А(х) и В(х).

Пр. y’’ + 2y’ – 3y = x.

а) Характеристическое уравнение k² + 2k – 3 = 0 имеет корни k₁ = 1, k₂ = -3. Частные решения однородного уравнения: y₁ = e^x, y₂ = e^-3x.

б) Частное решение неоднородного уравнения ищем в виде y* = A(x)e^x + B(x)e^-3x

и на производные от неизвестных функций A(x), B(x) накладываем условие (20)

A’(x)e^x + B’(x)e^-3x = 0 A’(x) = x/4 e^-x A(x) = ¼ = -(1+x)/4 e^-x

A’(x)e^x - 3B’(x)e^-3x = x B’(x) = - x/4 e^3x B(x) = -¼ = (1-3x)/36e^3x

Решим систему двух линейных уравнений, вычисляем интегралы и получаем частное решение неоднородного уравнения: y* = - x/3 –2/9. Проверка:

(- x/3 –2/9)``+ 2(- x/3 –2/9)` - 3(- x/3 –2/9) = x, т.е. x = x.

Общее решение исходного уравнения y = y₀ + y* = - x/3 –2/9 + C₁e^x + C₂e^-3x.

Дата добавления: 2017-01-13