
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Представление функции в виде совершенной дизъюнктивной и совершенной конъюнктивной формах. Разложение функции по начальному множеству переменных
|
|
|
|
Определение
Утверждение о числе функций от n переменных.
Определение
Определение
Определения.
Бинарная операция  ассоциативна, если тождественно выполняется:
ассоциативна, если тождественно выполняется:  ;
;
бинарная операция коммутативна, если тождественно выполняется: 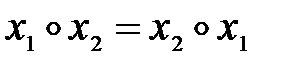 ;
;
бинарная операция  дистрибутивна по отношению к бинарной операции
дистрибутивна по отношению к бинарной операции  , если тождественно выполняется:
, если тождественно выполняется:
 ;
;
Утверждение 1. 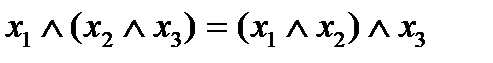 , конъюнкция ассоциативна.
, конъюнкция ассоциативна.
| x1 | x2 | x3 | x2  x3 x3
| x1  (x2 (x2  x3) x3)
| x1  x2 x2
| (x1  x2) x2)  x3 x3
|
| 1 | 1 |
Утверждение 2.  ,
,
дизъюнкция ассоциативна.
| x1 | x2 | x3 | x2  x3 x3
| x1  (x2 (x2  x3) x3)
| x1  x2 x2
| (x1  x2 ) x2 )  x3 x3
|
| 1 | 1 |
Утверждение 3. 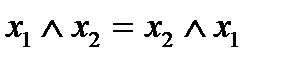 , конъюнкция
, конъюнкция
коммутативна;  , дизъюнкция также
, дизъюнкция также
коммутативна;
| x1 | x2 | x1  x2 x2
| x2  x1 x1
|
| 1 | 1 |
Предложение 1. Результат выполнения ассоциативной операции не зависит от расположения скобок в скобочном выражении.
Например: Если  ассоциативная операция, тогда
ассоциативная операция, тогда
 .
.
Доказательство предлагается в качестве домашнего упражнения.
Примечание: использовать индукцию по числу скобок в выражении.
Из того, что конъюнкции и дизъюнкции ассоциативные операции, результат конъюнкции или дизъюнкции нескольких переменных не зависит от расположения скобок.
|
|
|
Например: 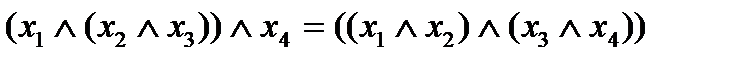
Тогда в силу независимости значения выражений конъюнкций от расположения скобок корректно определение 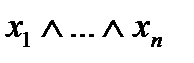 как значение логического произведения при каком-либо порядке расположения скобок. Точно также для дизъюнкции
как значение логического произведения при каком-либо порядке расположения скобок. Точно также для дизъюнкции  .
.
Предложение 2. Конъюнкция 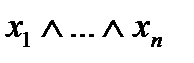 равна 0, т. и т.т., когда хотя бы один из множителей
равна 0, т. и т.т., когда хотя бы один из множителей 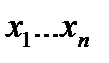 равен 0.
равен 0.
Дизъюнкция  равна 1, т. и т.т., когда хотя бы одно из слагаемых
равна 1, т. и т.т., когда хотя бы одно из слагаемых 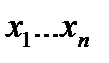 равно 1.
равно 1.
Доказательство предлагается в качестве домашнего упражнения.
Утверждение 4.
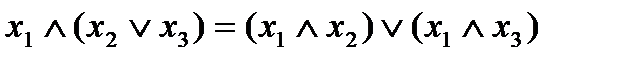 , конъюнкция дистрибутивна по отношению к дизъюнкции.
, конъюнкция дистрибутивна по отношению к дизъюнкции.
| x1 | x2 | x3 | x2  x3 x3
| x1  (x2 (x2  x3) x3)
| x1  x2 x2
| x1  x3 x3
| (x1  x2 ) x2 )  (x1 (x1  x3) x3)
|
| 1 | 1 |
Утверждение 5.
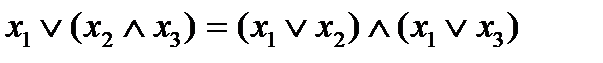 , дизъюнкция дистрибутивна по отношению к конъюнкции.
, дизъюнкция дистрибутивна по отношению к конъюнкции.
| x1 | x2 | x3 | x2  x3 x3
| x1  (x2 (x2  x3) x3)
| x1  x2 x2
| x1  x3 x3
| (x1  x2) x2)  (x1 (x1  x3) x3)
|
| 1 | 1 |
Утверждение 6. 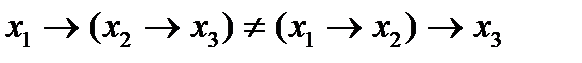 , следствие не ассоциативная операция.
, следствие не ассоциативная операция.
| x1 | x2 | x3 | x2  x3 x3
| x1  (x2 (x2  x3) x3)
| x1  x2 x2
| (x1  x2) x2)  x3 x3
|
| 0 | ||||||
| 1 | 1 |
Утверждение 7. 
| x1 | x2 | x3 | x2  x3 x3
| x1 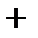 (x2 (x2  x3) x3)
| x1+x2 | x1+x3 | (x1+x2)  (x1+x3) (x1+x3)
|
| 0 | 0 |
Утверждение 8.
|
|
|
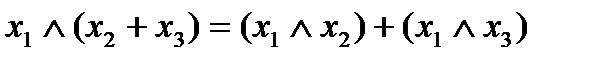 ,
,
конъюнкция дистрибутивна по отношению к сумме по модулю два.
| x1 | x2 | x3 | x2+x3 | x1  (x2+x3) (x2+x3)
| x1  x2 x2
| x1  x3 x3
| (x1  x2)+(x1 x2)+(x1  x3) x3)
|
| 1 | |||||||
| 0 | 0 |
Определение. Две функции назовем одинаковыми, если они зависят от одного и того же набора переменных и их значения совпадают на каждом из наборов своих переменных.
Переменная x булевой функции f(x…) называется существенной, если существует набор значений остальных переменных функции, что изменение значения переменной при данном наборе остальных переменных изменяет значение функции.
Пример: x1 и x2 - существенные переменные (x1 по 8 –му и по 5-му наборам; x2
по 6 и 8 наборам).
x3 - не существенная переменная
| x1 | x2 | x3 | f |
| 1 | |||
Две функции равны, если они одинаковы после отбрасывания несущественных переменных.
Теорема: Число различных (неодинаковых) булевых функций от n переменных есть 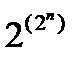 .
.
Теорема будет следовать из следующего утверждения:
число различных двоичных наборов длины n есть 2n (под длиной набора подразумевается число цифр в нем).
Докажем утверждение индукцией по длине n набора.
Для n=1 имеем 0;1 два различных набора длины 1;
21 =2. Для n=1 утверждение индукции справедливо.
Пусть утверждение индукции справедливо для n³1, то есть число различных двоичных наборов длины n³1 есть - 2n.
Покажем справедливость утверждения для n=n+1. Разобьем все двоичные наборы длины n+1 на две группы. В первую группу отнесем двоичные наборы, которые начинаются на 0. Во вторую группу отнесем двоичные наборы, которые начинаются на 1, например, для n+1 = 3 будет такое разбиение:
Двоичные наборы первой (второй) группы получаются из всевозможных двоичных наборов длины n добавлением слева нуля (единицы) к всевозможным наборам длины n.
|
|
|
Но по предположению индукции наборов длины n имеется 2n, поэтому число наборов как в первой, так и во второй группе будет 2n, поэтому общее число наборов длины (n+1) будет 2n+2n = 2n 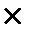 2 = 2n+1
2 = 2n+1
Утверждение доказано.
| x1 | … | xn | f(x1…xn) | |
| 0 | … | * | ||
| … | … | … | |
| … | * |
Функций от n переменных будет ровно столько, сколько существует разных двоичных наборов длины 2n.
По предыдущему утверждению это число есть  . Теорема доказана.
. Теорема доказана.
Определение:
Элементарной конъюнкцией на множестве переменных {x1…xn} называют функцию логического произведения множителей, где каждый множитель либо переменная, либо отрицание переменной.
В дальнейшем значение  в элементарной конъюнкции будем опускать или заменять
в элементарной конъюнкции будем опускать или заменять  .
.
Например: { x1 x2 x3 x4 }
x1 x2 x4 ; эта функция равна 1, только на одном наборе:
1 0 1 x1  x2
x2  x4=1
x4=1
x1 x2 x4
Рангом конъюнкции называют число переменных конъюнкции. Далее будем считать, что все переменные в множителях элементарных конъюнкций различны. В противном случае, используя правила:  , приведем конъюнкции к нужном виду;
, приведем конъюнкции к нужном виду;
Например: 
полученная конъюнкция будет тождественно равна первоначальной.
В силу коммутативности и ассоциативности бинарной конъюнкции, две приведенные конъюнкции равны, т. и т. т., когда они состоят из одного набора множителей.

Элементарной дизъюнкцией на множестве переменных {x1…xn} называют функцию логического сложения слагаемых, где каждое слагаемое либо переменная, либо отрицание переменной.
Например: { x1 x2 x3 x4 
x1  x2
x2  x4 ; эта функция равна 0, т. и т.т., когда все слагаемые равны 0. т.е. на наборах 0110 и 0100
x4 ; эта функция равна 0, т. и т.т., когда все слагаемые равны 0. т.е. на наборах 0110 и 0100
Рангом дизъюнкции называют число слагаемых дизъюнкции. Далее будем считать, что все переменные в множителях элементарных дизъюнкций различны. В противном случае, используя правила:
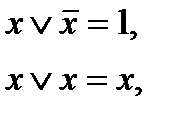
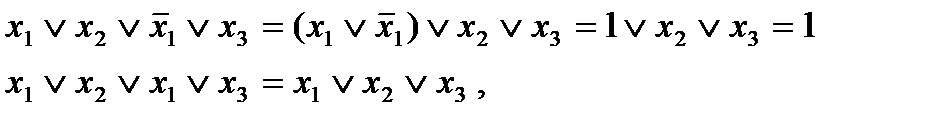
приведем дизъюнкции к нужном виду; полученная дизъюнкция будет тождественно равна первоначальной.
|
|
|
В силу коммутативности и ассоциативности элементарные дизъюнкции равны, т. и т. т., когда они состоят из одного и того же набора слагаемых.
Дизъюнктивной нормальной формой (ДНФ) на множестве переменных (x1…xn) называют функцию логического сложения некоторых слагаемых, где каждое слагаемое есть элементарная конъюнкция на (x1…xn):
{ x1 x2 x3 x4 }

ДНФ называется совершенной (СДНФ), если каждая элементарная конъюнкция имеет ранг n:
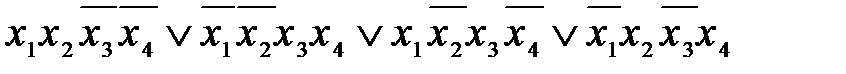
Далее считаем, что слагаемые ДНФ не повторяются (в противном случае можно
Множество единиц ДНФ есть объединение множества единиц элементарных конъюнкций ДНФ. Каждая элементарная конъюнкция полного ранга имеет единственную единицу. Слагаемые СДНФ (элементарные конъюнкции полного ранга) и единицы СДНФ находятся во взаимнооднозначном соответствии.
Теорема о представлении любой булевой функции в виде СДНФ: для любой булевой функции справедлива следующая формула:

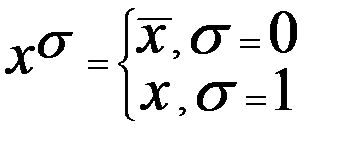
| x1 | x2 | x3 | f | |
| 0 | 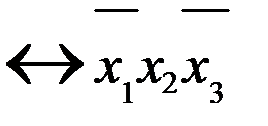
| |||
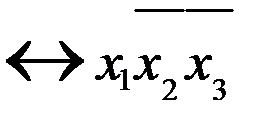
| ||||
| 1 | 
| |||
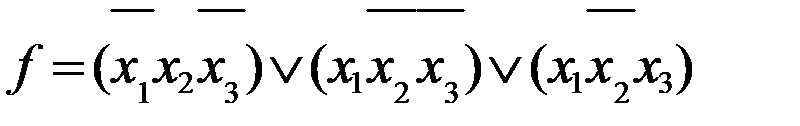
Доказательство:
Свойства 

1)
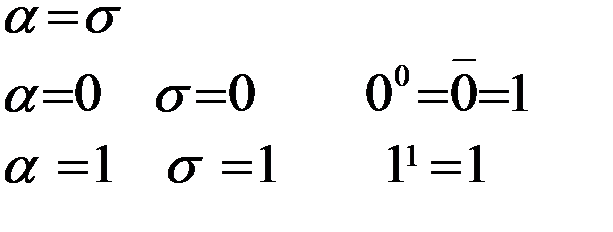
2)

Чтобы доказать теорему покажем выполнение данного равенства на любом двоичном наборе,то есть что левые и правые части совпадают для любого двоиного набора:
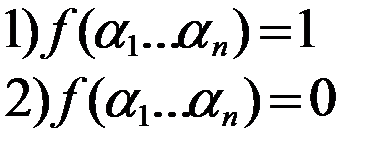 .
.
 . То есть левая часть равенства равна 1. Покажем,что и правая часть равенства также равна 1 на данном наборе. Для этого достаточно показать,что хотя бы одно слагаемое правой части равно 1.
. То есть левая часть равенства равна 1. Покажем,что и правая часть равенства также равна 1 на данном наборе. Для этого достаточно показать,что хотя бы одно слагаемое правой части равно 1.
Таким слагаемым будет слагаемое, которое соответствует единичному набору s, совпадающего с набором a.
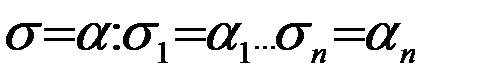 .
.
Значение этого слагаемого на наборе 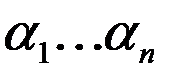 есть
есть
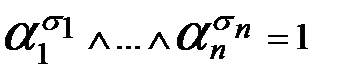 в силу того,что значение каждого множителя равно 1. Последнее справедливо в силу свойства символа
в силу того,что значение каждого множителя равно 1. Последнее справедливо в силу свойства символа  .
.
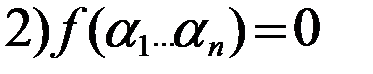 . То есть левая часть равна 0. Покажем, что и правая часть также равна 0. Для этого нужно показать, что значение всех слагаемых равно 0. Рассмотрим произвольное слагаемое правой части, которое соответствует некоторому двоичному набору
. То есть левая часть равна 0. Покажем, что и правая часть также равна 0. Для этого нужно показать, что значение всех слагаемых равно 0. Рассмотрим произвольное слагаемое правой части, которое соответствует некоторому двоичному набору 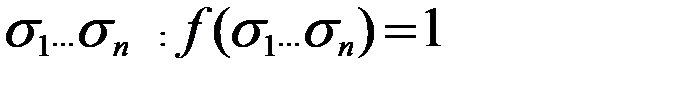 , тогда
, тогда 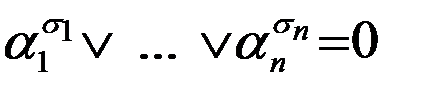 в силу, того, что наборы a и s различны, т.к. a - набор, на котором значение функции равно 0, а s - набор, на котором значение функции равно 1. Так как наборы различны, то существует множитель i:
в силу, того, что наборы a и s различны, т.к. a - набор, на котором значение функции равно 0, а s - набор, на котором значение функции равно 1. Так как наборы различны, то существует множитель i:  , а поэтому и все произведение равно 0.Таким образом каждое слагаемое равно 0, следовательно и вся сумма равна 0, значит правая часть равна 0.
, а поэтому и все произведение равно 0.Таким образом каждое слагаемое равно 0, следовательно и вся сумма равна 0, значит правая часть равна 0.
Теорема полностью доказана.
| x1 | x2 | x3 | f | 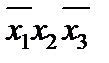
| 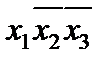
| 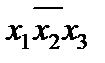
| 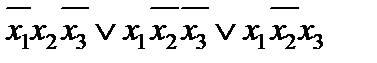
|
Теорема о разложении булевой функции по первым k-переменным.

Доказательство:
Рассмотрим произвольный набор значений переменных  , и покажем, что левая и правая часть равны. Левая часть -
, и покажем, что левая и правая часть равны. Левая часть - 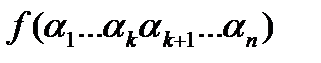 .
.
В правой части рассмотрим слагаемое, в котором значение набора s совпадает с первыми k-компонентами набора a: 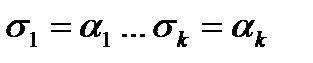 .
.
Значение этого слагаемого на наборе 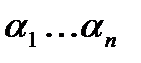 равно
равно 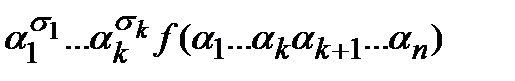 .
.
В силу того, что набор s и первые k-компонент набора a совпадают, рассматриваемые множители равны 1, все слагаемое равно  . Все остальные слагаемые равны 0 в силу того, что среди множителей
. Все остальные слагаемые равны 0 в силу того, что среди множителей 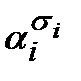 обязательно найдется множитель, в котором a и s различаются, а это нулевой множитель. Поэтому правая часть равна
обязательно найдется множитель, в котором a и s различаются, а это нулевой множитель. Поэтому правая часть равна  (все слагаемые, кроме быть может одного, равны 0).
(все слагаемые, кроме быть может одного, равны 0).
Теорема доказана.
Нетрудно убедиться в справедливости следующих тождеств:
1) 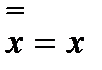 6)
6) 
2)  7)
7) 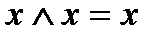
3) 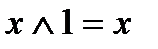 8)
8) 
4)  9)
9) 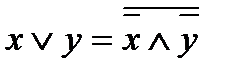
5)  10)
10) 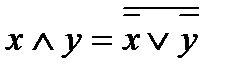
Доказательство предлагается в качестве домашних упражнений.
Последние два тождества называются правилами Де-Моргана.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 676; Нарушение авторских прав?; Мы поможем в написании вашей работы!