
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрическая интерпретация двоичных функций. 1 страница
|
|
|
|
Пример.
Предполные классы двоичных функций.
4)
3).
2).
L
L
М
М
S
S
M M
M M
M M
Монотонные функции M.
S S
S S
S S
Самодвойственные функции S.
Сохраняющие единицу- T1.
T0 : 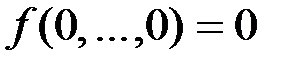 T1:
T1: 
 T0,
T0,  T1
T1
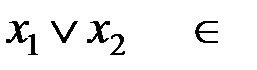 T0,
T0,  T1
T1
 T0 ,
T0 ,  T1
T1
 T0,
T0,  T1
T1
 T0,
T0,  T1
T1
 T0 ,
T0 ,  T1
T1
 T0 ,
T0 ,  T1
T1
 T0,
T0,  T1
T1
Определение: 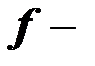 называется самодвойственной, если совпадает с двойственной к ней функцией.
называется самодвойственной, если совпадает с двойственной к ней функцией.
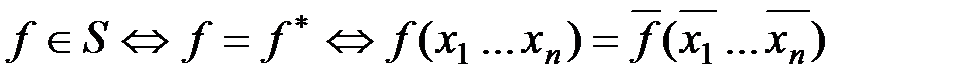 .
.
Очевидно эквивалентное определение самодвойственной функции:
Определение:  S,если принимает противоположные значения на противоположных наборах.
S,если принимает противоположные значения на противоположных наборах.
| x1 | x2 | x3 | f(x1x2x3)  S S
|
| 0 | |||
| 0 | |||
| 0 | |||
Пример:
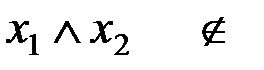 S
S  S
S
Определение: набор 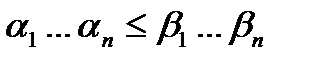 , если
, если  ;
;
Например: 
наборы 0101 и 1001 не сравнимы.
Определение:  M, если
M, если 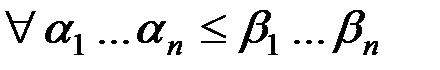 :
:
 .
.
| x |
| x1 |
| x2 |
| y |
| x1 | x2 | x3 | f(x1x2x3)  M M
| 
|
Метод определения монотонности функции f:
Рассматриваем все наборы, на которых значение 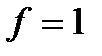 . Для этих наборов рассматриваем наборы большие, и если среди больших наборов нет нуля функции, тогда функция монотонна. В противном случае она не монотонная. Корректность этого метода следует непосредственно из определения монотонной функции.
. Для этих наборов рассматриваем наборы большие, и если среди больших наборов нет нуля функции, тогда функция монотонна. В противном случае она не монотонная. Корректность этого метода следует непосредственно из определения монотонной функции.
| x1 | x2 | x3 | f(x1x2x3)  M M
|
Для данной функции для единицы 001 большие наборы есть 101, 011, 111. Среди них есть ноль, набор 011. Поэтому функция немонотонная.
|
|
|
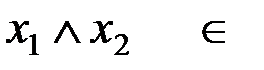 M
M 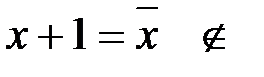 M
M
Линейные функции L.
Определение: линейные функции – функции, степень полинома Жегалкина которых не больше единицы.
Определение: степенью полинома Жегалкина называется максимальное число переменных в слагаемых этого полинома.
Степень 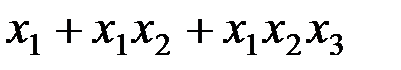 равна 3.
равна 3.
Степень  равна 1.
равна 1.
Степень 1 равна 0; степень 0 равна 0.
| x1 | x2 | x3 | 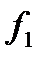 
| 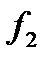
|
Методы определения линейности функции f:
1.Способ Находим полином Жегалкина функции f и определяем его степень. Если степень 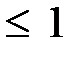 , то функция линейная. В противном случае функция нелинейная.
, то функция линейная. В противном случае функция нелинейная.
2. Способ. Определяем существенные переменные функции f и рассматриваем две возможные линейные функции: сумма найденных существенных переменных и сумма существенных переменных плюс 1. Если исходная функция совпадает с одной из данных двух, то функция линейна. В противном случае функция нелинейная.
Корректность данного метода следует из факта, что у линейной функции 
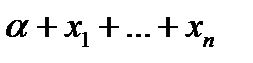 все переменные
все переменные 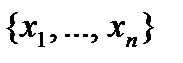 существенные и других существенных нет.
существенные и других существенных нет.
1) x1 - существенная (по 1-ому и 5- ому),x2 - существенная (по 3- ему и по 1-ому набору), x3 не существенная. Если функция линейная, то она имеет вид либо x1+x2, либо x1+x2+1; подходит первое выражение, поэтому первая функция линейная.
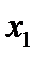
| 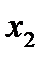
| 
| 
|
вторая функция нелинейная
2) x1 - существенная (по 4-ому и 8-ому),x2- существенная (по 6-ому и 8-ому), x3 не существенная:
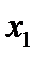
| 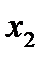
| 
| 
| 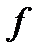
|
вторая функция нелинейная
Утверждение: все перечисленные пять классов являются замкнутыми, то есть суперпозиция любых двух функций из каждого класса является функцией тогоже класса.
|
|
|
Доказательство:
1) T0
Рассмотрим  T0
T0
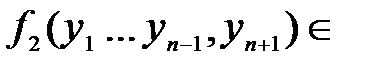 T0
T0
Рассмотрим суперпозицию
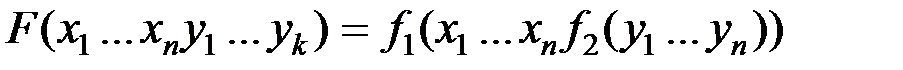 и покажем, что полученная
и покажем, что полученная  T0. Для этого найдем значение
T0. Для этого найдем значение  на нулевом наборе:
на нулевом наборе:

2) T1
Рассмотрим 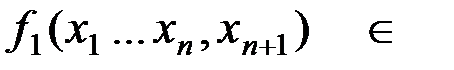 T1
T1
 T1
T1
Рассмотрим 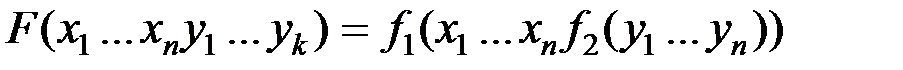 :
:

Рассмотрим 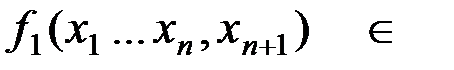 S
S
Рассмотрим 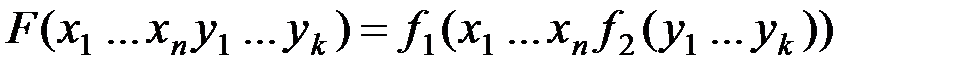 :
:

Рассмотрим  М
М
Рассмотрим суперпозицию
 :и
:и
рассмотрим произвольную пару сравнимых наборов 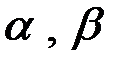 и
и 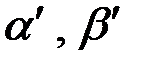 :
: 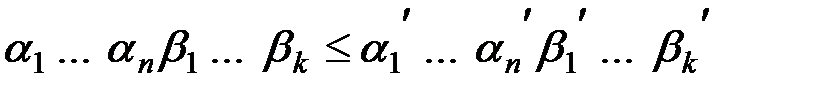 и покажем, что выполнено:
и покажем, что выполнено: 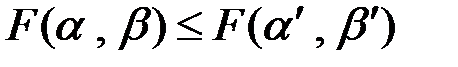 .
.
Нетрудно видеть, что из того, что  следует, что
следует, что  и
и  .
.
В силу того, что:
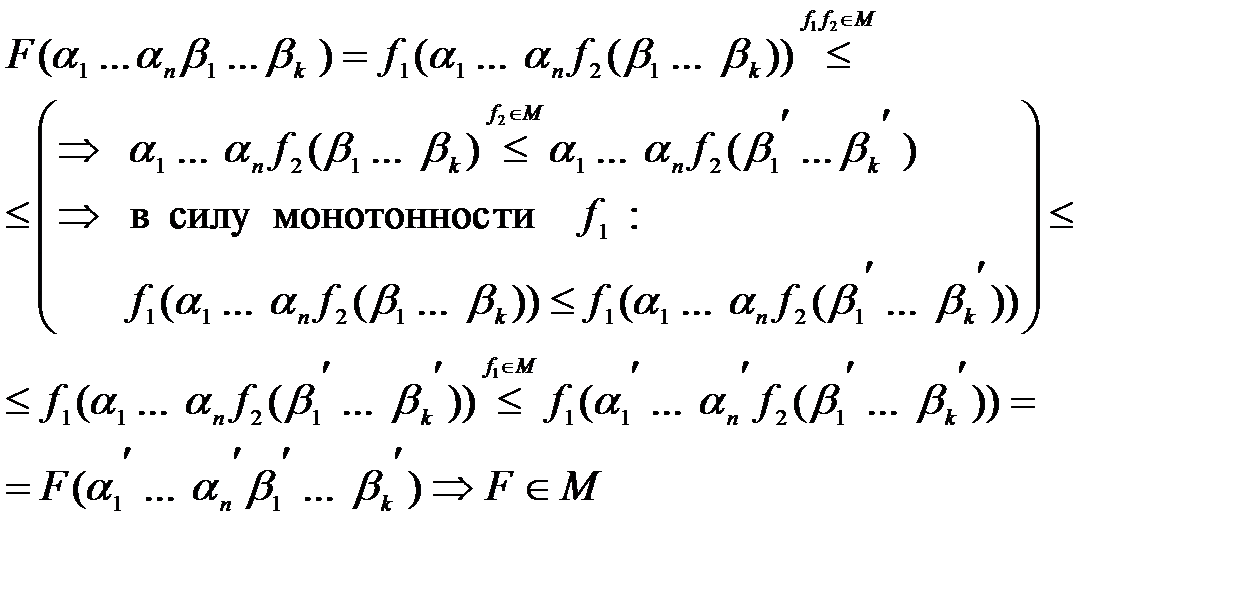
Рассмотрим 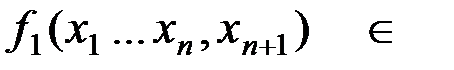 L
L
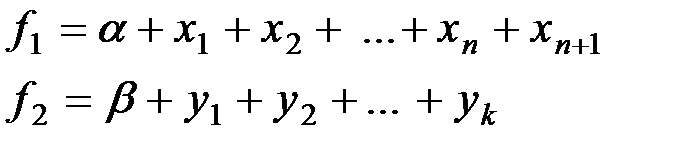 , где α и β - некоторые константы.
, где α и β - некоторые константы.
Рассмотрим 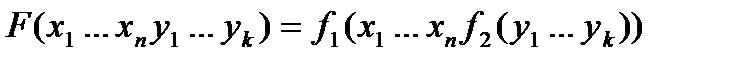 .
.
 .
.
Используя ассоциативность и коммутативность операции +, преобразуем к виду:
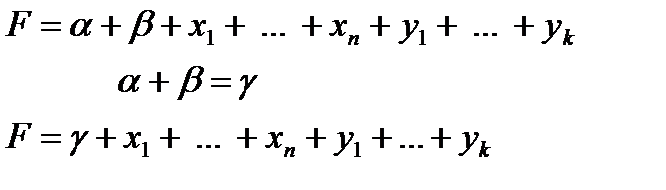 .
.
Степень  не превосходит 1, следовательно
не превосходит 1, следовательно  L.
L.
Замечание Приведенные выше рассуждения будут справедливы, если множества переменных подставляемых функций пересекаются.
Упражнение Покажите, что переименование переменных не выводит функции из классов
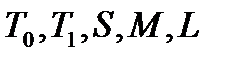 .
.
1.6 Критерий полноты в класее двоичных функций относительно суперпозиций функций.
Для того, чтобы система  была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти классов: T0, T1, S, M, L.
была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти классов: T0, T1, S, M, L.
Проблема полноты: по заданной системе функции ответить на вопрос, является ли эта система полной, т.е. можно ли с помошью всевозможных суперпозиций данных функций получить любую булевую функцию.
Проверим вначале критерий Поста на известных примерах, а затем докажем его справедливость в общем случае.
Пример:  .
.
По теореме о представлении любой булевой функции в виде СДНФ данная система полна. И в тоже время система не содержится ни в одном из классов T0, T1, S, M, L, поэтому критерий Поста справедлив для данной системы.
Пример: 

Полнота данной системы следует из теоремы о представлении любой булевой функции в виде полинома Жегалкина, и вновь критерий Поста справедлив для данной системы, т.к. система не принадлежит ни одному из пяти классов.
Пример: 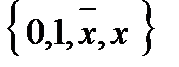 - не полная, так как
- не полная, так как 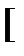
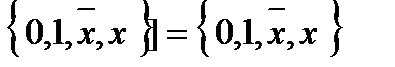
и критерий Поста справедлив для данной системы, т.к. 
 L.
L.
Доказательство:
Необходимость: пусть система K полна.
Покажем, что она не принадлежит ни одному из пяти классов. Допустим противное: система принадлежит одному из пяти классов. Пусть K  T0 . Т.е. все функции K сохраняют 0. Но тогда и любая суперпозиция функций из K будет сохранять 0. Но тогда
T0 . Т.е. все функции K сохраняют 0. Но тогда и любая суперпозиция функций из K будет сохранять 0. Но тогда 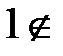 [K], и K - неполная. Пусть K
[K], и K - неполная. Пусть K  T1, тогда любая суперпозиция из K сохраняет 1, тогда
T1, тогда любая суперпозиция из K сохраняет 1, тогда 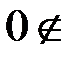 [K]. Пусть K
[K]. Пусть K  S, тогда суперпозиция любых функций будет самодвовойственна, тогда
S, тогда суперпозиция любых функций будет самодвовойственна, тогда 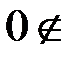 [K].
[K].
|
|
|
Пусть K  M, тогда
M, тогда 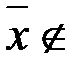 [K]. Пусть K
[K]. Пусть K  L, тогда
L, тогда 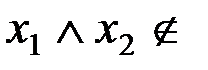 [K]. Получаем противоречие (система не является полной, в силу замкнутости классов T0, T1, S, M, L относительно суперпозиций).
[K]. Получаем противоречие (система не является полной, в силу замкнутости классов T0, T1, S, M, L относительно суперпозиций).
Достаточность: пусть система K не содержится ни в одном из пяти классов, т.е.
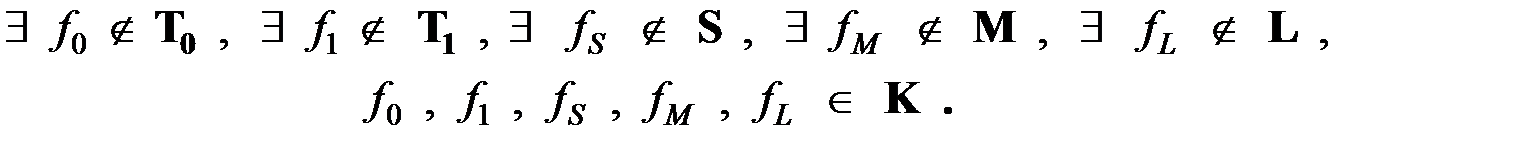
Построим заведомо полную систему  .
.
I этап: 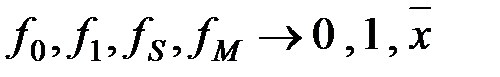
II этап: 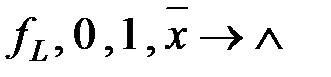
I этап:  и
и  , и переименуем все их переменные в
, и переименуем все их переменные в  :
: 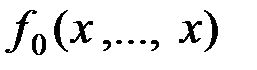 и
и  :
:
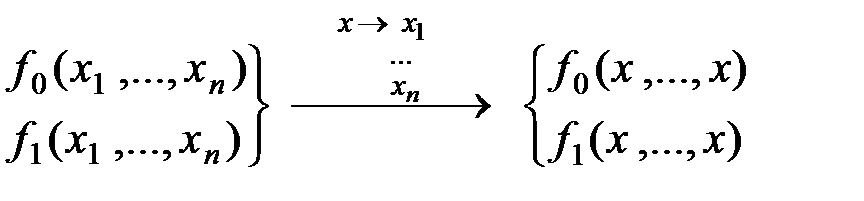
| X | f0 | f1 |
| 1,0 | ||
| 1,0 |
Теперь имеем четыре возможных случая в зависимости от значений функций  и
и 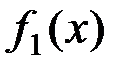 в 1 и в 0 соответственно.
в 1 и в 0 соответственно.
1) 
2) 
3) 
4) 
Простейшими окажутся 1) и 4).
Рассмотрим 1) и 4) случаи.
1 случай:
| X | f0 | f1 |
т.е. 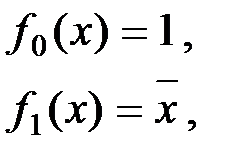

4 случай:
| X | f0 | f1 |
т.е. 
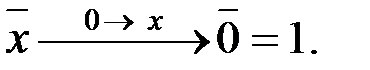
Остались 2) и 3)
2 случай:
| X | f0 | f1 |
т.е. 
Построим вывод:
 .
.
 M, следовательно по определению существует пара наборов (нижний строго больше верхнего), а значение функции наоборот:
M, следовательно по определению существует пара наборов (нижний строго больше верхнего), а значение функции наоборот: 

Разобьем множество переменных  на два множества
на два множества  и
и  .
.
 - переменные, которые не изменяются в двух данных наборах, а
- переменные, которые не изменяются в двух данных наборах, а  - все остальные переменные:
- все остальные переменные:
 И теперь все переменные множества
И теперь все переменные множества  переименнуем в x, а во все переменные множества
переименнуем в x, а во все переменные множества  подставим соответствующие константы:
подставим соответствующие константы:
 .
.
Тогда полученная функция одного аргумента  в нуле будет равна значению первоначальной функции на верхнем наборе, т.е. единице, а в единице равна значению первоначальной функции на нижнем наборе, т.е. нулю. Это и есть
в нуле будет равна значению первоначальной функции на верхнем наборе, т.е. единице, а в единице равна значению первоначальной функции на нижнем наборе, т.е. нулю. Это и есть  .
.  .
.
Например, пусть наборы были:
| X1 | x2 | X3 | x4 | x5 | fM |


3 случай:
| X | f0 | f1 |
т.е. 
Построим вывод:

Пусть  и
и  - пара противоположных наборов, на которых значение функции
- пара противоположных наборов, на которых значение функции 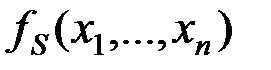 одно и то же, и равно, для определенности нулю:
одно и то же, и равно, для определенности нулю: 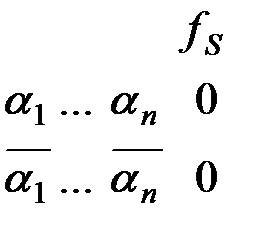 .
.
Разобьем множество всех переменных на две группы. В первую  отнесем все переменные, которые равны нулю в первом наборе, во вторую
отнесем все переменные, которые равны нулю в первом наборе, во вторую  , которые равны единице в первом наборе:
, которые равны единице в первом наборе:
|
|
|
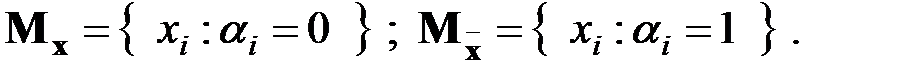
Теперь в переменные  подставим x, а в
подставим x, а в  подставим
подставим  :
:  .
.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 320; Нарушение авторских прав?; Мы поможем в написании вашей работы!