
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрическая интерпретация двоичных функций. 2 страница
Нетрудно видеть, что полученная функция есть константа 0, т.к. данная функция в нуле равна значению первоначальной функции на первом наборе, т.е. нулю, а в единице равна значению первоначальной функции на втором наборе, т.е. нулю. Константу 1 получим подстановкой 0 в функцию  .
.
Например, пусть пара противоположных наборов, на которых  равна нулю, имеют вид:
равна нулю, имеют вид:
| X1 | x2 | X3 | x4 | x5 | f |
Тогда  .
.
I-ый этап завершен.
II этап:
Построим вывод:

Рассмотрим полином Жегалкина  функции
функции  .
.  .
.
В силу того, что  - нелинейная, полином содержит по крайней мере одно слагаемое, которое есть конъюнкция по крайней мере двух переменных. Для определенности будем считать, что эта конъюнкция первых двух переменных. Используя дистрибутивность умножения относительно суммы, сгруппируем слагаемые следующим образом.
- нелинейная, полином содержит по крайней мере одно слагаемое, которое есть конъюнкция по крайней мере двух переменных. Для определенности будем считать, что эта конъюнкция первых двух переменных. Используя дистрибутивность умножения относительно суммы, сгруппируем слагаемые следующим образом.
Из всех слагаемых, содержащих  и
и  вынесем за скобку конъюнкцию этих двух переменных
вынесем за скобку конъюнкцию этих двух переменных  ; полином в скобках обозначим
; полином в скобках обозначим  ; из всех слагаемых, содержащих только
; из всех слагаемых, содержащих только 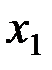 ,
,
вынесем за скобку  :
:  ; из всех слагаемых, содержащих
; из всех слагаемых, содержащих  , вынесем
, вынесем  :
: 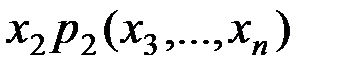 ; останутся слагаемые, которые не содержат ни
; останутся слагаемые, которые не содержат ни  , ни
, ни  , обозначим этот полином
, обозначим этот полином  .
.

Из единственности полинома Жегалкина следует, что существует значение  переменных
переменных  , при котором
, при котором  . Совершим соответствующие подстановки констант в нелинейную функцию
. Совершим соответствующие подстановки констант в нелинейную функцию 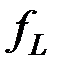 .
.
 Таким образом, получили функцию
Таким образом, получили функцию 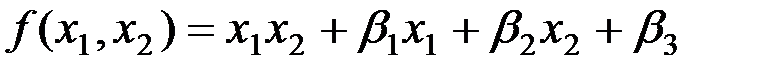 ,
,
где  некоторые константы.
некоторые константы.
Имеем восемь случаев:
| b1 | b2 | b3 | f(x1,x2) |

| |||
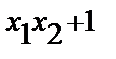
| |||
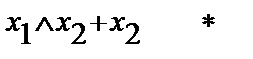
| |||
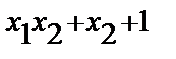
| |||
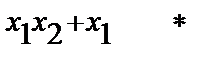
| |||
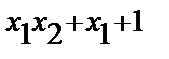
| |||
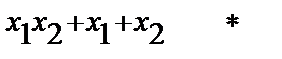
| |||

|
На самом деле достаточно рассмотреть всего лишь четыре случая, а именно, случай  сводится к случаю, когда
сводится к случаю, когда  подстановкой соответствующей функции в функцию отрицания
подстановкой соответствующей функции в функцию отрицания  .
.
Таким образом, достаточно рассмотреть случаи:
1) 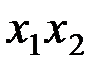 ; 2)
; 2)  ; 3)
; 3) 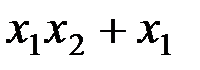 ; 4)
; 4)  .
.
1) 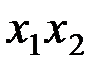
Требуемая конъюнкция получена.

Например, из  получим
получим 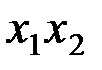 . После группировки слагаемых получаем
. После группировки слагаемых получаем  , полином
, полином  равен 1, например, если
равен 1, например, если  ,
,  . Подставляем 1 в
. Подставляем 1 в  , 0 в
, 0 в  , получаем функцию
, получаем функцию 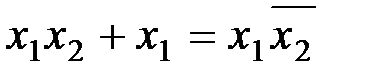 . Подставляем
. Подставляем  в переменную
в переменную  , получаем
, получаем 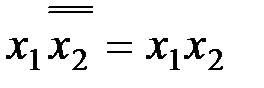 .
.
Упражнение 1: Исследовать на полноту:
1) 
2) 
3) 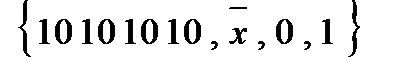
4) 
5) 
6) 
Упражнение 2: Получить из функции  функции
функции 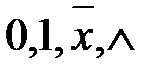 .
.
1)  2)
2) 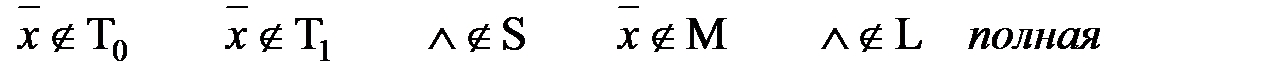 4)
4)  5)
5)  не полная
6)
не полная
6)  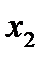  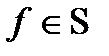 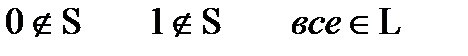 0 0 0 1 1
0 0 1 0 0
0 1 0 1 0
0 1 1 0 0
0 0 0 1 1
0 0 1 0 0
0 1 0 1 0
0 1 1 0 0  1 0 0 1 0
1 0 1 0 0
1 1 0 1 0
1 1 1 0 0
1 0 0 1 0
1 0 1 0 0
1 1 0 1 0
1 1 1 0 0 
|
Примеры:
1) Исследовать на полноту систему  :
:
| T0 | T1 | S | M | L | |
| f1 | - | + | - | - | - |
| f2 | - | ||||
| f3 |
2) Исследовать на полноту систему
 :
:
| T0 | T1 | S | M | L | |
| f1 | + | - | - | + | + |
| f2 | - | + | + | ||
| f3 | + | - | |||
| f4 | + | - | |||
| f5 | + |
Система неполная, т.к.  и
и  монотонны, то и суперпозиция этих функций монотонны,поэтому пятая функция тоже монотонна.
монотонны, то и суперпозиция этих функций монотонны,поэтому пятая функция тоже монотонна.
Система принадлежит монотонному классу, поэтому неполна.
3) Можно ли из системы функций
 получить функцию 0:
получить функцию 0:
| T0 | T1 | S | M | L | |
| f1 | - | - | + | - | + |
| f2 | + | ||||
| f3 | + | + |

Система принадлежит классу самодвойственных функции, в силу замкнутости этого класса, и в силу несамодвойственности 0, получить 0 из функций системы нельзя.
4) Можно ли из системы функций
 получить
получить  и
и  , и если «да», опишите определяющие выражения:
, и если «да», опишите определяющие выражения:
| T0 | T1 | S | M | L | |
| f1 | + | - | - | - | |
| f2 | - | ||||
| f3 | - |
Система полная, поэтому получить можно любые функции.
I: 
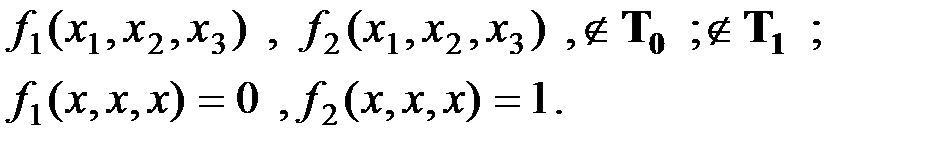
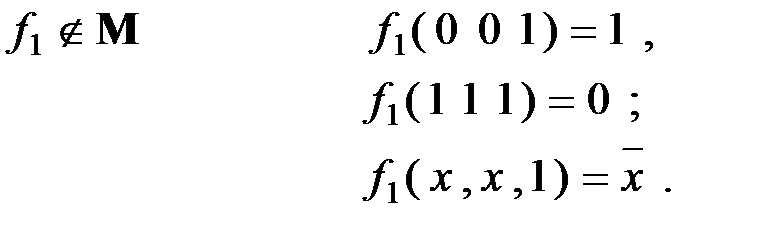
II: 
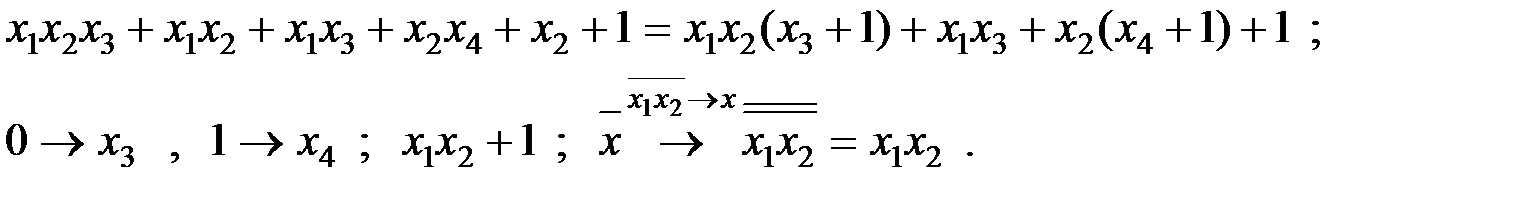
5) Можно ли из системы функций
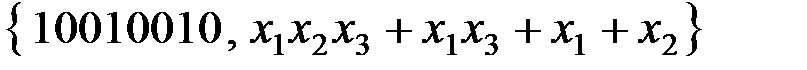 получить функции
получить функции
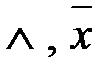 , и если “да”, опишите определяющие выражения:
, и если “да”, опишите определяющие выражения:
| T0 | T1 | S | M | L | |
| f1 | - | - | - | - | |
| f2 | - |
| x1 | x2 | x3 | f1 |
| 0 - | |||
| 0 - | |||
I: 

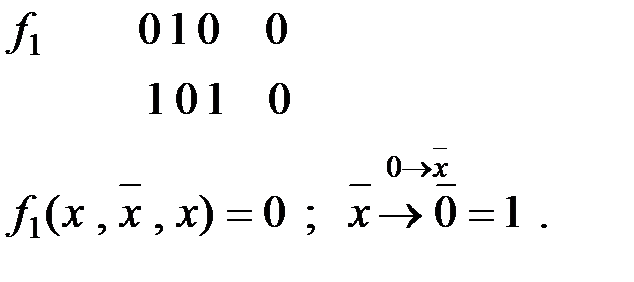

Упражнения: Исследовать на полноту системы:
1)  ; 2)
; 2)  ; 3)
; 3) 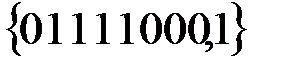 ;
;
4)  ; 5)
; 5) 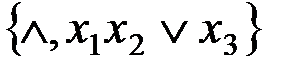 ;
;
Можно ли из соответствующих систем функций получить следующие функции, и если “да”, то напишите определяющее выражение:
6) из системы функций 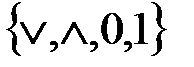 получить функцию
получить функцию  ;
;
7) из системы функций 
получить функцию 0;
8) из системы функций  получить функции
получить функции  ;
;
9) из системы функций
 получить функции
получить функции
 ;
;
10) из системы функций  получить функции
получить функции  ;
;
Определение:
Предполным классом К называется неполный класс, при добавлении любой функции  , которая не принадлежит ему, получается класс полный.
, которая не принадлежит ему, получается класс полный.

Утверждение:
Предполный класс является замкнутым.
Доказательство: Допустим противное, что некоторый предполный класс К не замкнут: 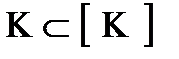 , тогда рассмотрим функцию
, тогда рассмотрим функцию

|
 f f
|
т.е. [ K,f ] не полный
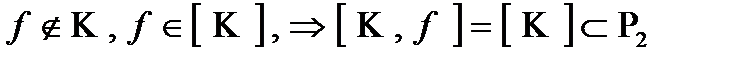
Теорема:
В классе булевых функций  есть ровно пять предполных классов:
есть ровно пять предполных классов:  .
.
Доказательство:
В начале покажем, что данные классы являются предполными, а затем покажем, что других предполных классов нет.
1) Рассмотрим  .
.
Данный класс содержит функции:

 поэтому класс Т0 не принадлехит классам Т1, S, М, L.
поэтому класс Т0 не принадлехит классам Т1, S, М, L.
Рассмотрим произвольную  , тогда
, тогда  не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно класс
не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно класс  является предполным.
является предполным.
2) Рассмотрим Т1:

Рассмотрим произвольную  не принадлежит ни одному из пяти классов, следовательно по теореме Поста является полной, следовательно
не принадлежит ни одному из пяти классов, следовательно по теореме Поста является полной, следовательно  предполный.
предполный.
3) Рассмотрим S:
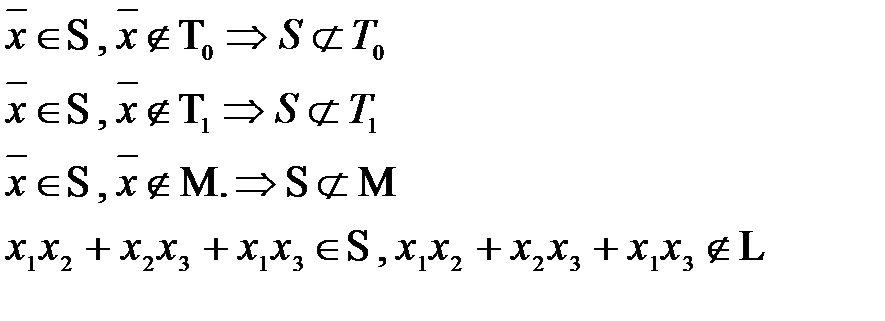
Рассмотрим  не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно
не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно  предполный.
предполный.
4) Рассмотрим  :
:
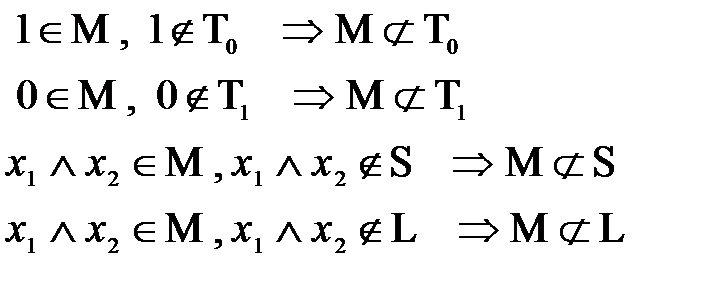
Рассмотрим  не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно
не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно  предполный.
предполный.
5) Рассмотрим L:
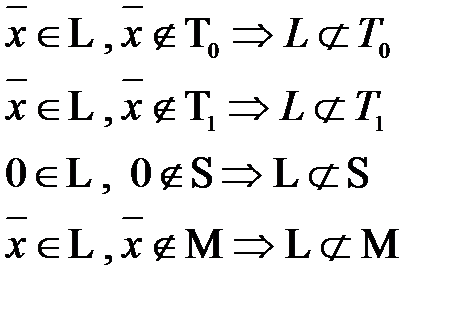
Рассмотрим  не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно
не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно 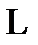 предполная. Все перечисленные классы не полны по теореме Поста.
предполная. Все перечисленные классы не полны по теореме Поста.
Покажем, что других предполных классов в  нет.
нет.
Допустим противное, что  - предполный:
- предполный:
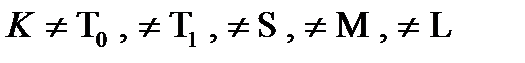 , следовательно в данном классе
, следовательно в данном классе  :
:

|

|
| РИС.1 |
в силу того, что класс  - предполный, следовательно включение на рис.1 невозможно, т.к. если бы было наоборот, то рассмотрим
- предполный, следовательно включение на рис.1 невозможно, т.к. если бы было наоборот, то рассмотрим  , мы бы получили, что все функции системы
, мы бы получили, что все функции системы 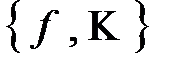 сохраняют 0, поэтому полной система
сохраняют 0, поэтому полной система  не является, следовательно
не является, следовательно  не является предполным.
не является предполным.
По этой же причине в классе 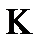 должна быть,
должна быть,  , должна быть
, должна быть  , должна быть
, должна быть  , должна быть
, должна быть 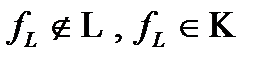 , следовательно из этих включений следует, что система
, следовательно из этих включений следует, что система 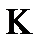 является полной, противоречие с предполнотой этой системы.
является полной, противоречие с предполнотой этой системы.
Упражнения:
Найдите определяющие выражения функций через суперпозиции функций системы.
1) 
2) 
3) 
4) 
5) 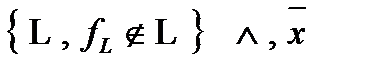
Определение:
Полной системой бул. функций в замкнутом классе К является система функций, которая принадлежит данному классу, и замыкание которой совпадает с самим классом
 .
.
Определение:
Базисом в замкнутом классе К называют систему В, которая полна в этом классе, но любая собственная подсистема полной в классе не является.
Пример 1: Рассмотрим множество всех булевых функций Р2. В этом множестве рассмотрим систему  .Эта система полна по т. Поста.
.Эта система полна по т. Поста.
Чтобы определить,что все собственные подсистемы не полны, достаточно рассмотреть лишь максимальные по включению собственные подсистемы данной, получаемые из данной удалением какой-либо функции.
Если ни одна из этих подсистем не является полной, то полной не является и любая другая собственная подсистема (докажите предыдущие утвеждения)

В данном примере максимальные собственные подсистемы не полны, значит  является базисом в Р2.
является базисом в Р2.
Пример 2: Является ли система  базисом в Р2?
базисом в Р2?
 , поэтому система полна, но собственная подсистема
, поэтому система полна, но собственная подсистема  также полна, поэтому данная система не базис в Р2.
также полна, поэтому данная система не базис в Р2.
Определение:
Скажем, что функция f не зависима от системы  , если эта функция не принадлежит замыканию системы:
, если эта функция не принадлежит замыканию системы:  .
.
Пример 1: Рассмотрим функцию  и систему
и систему 
 :
:
Утверждаем, что  не зависит от этой системы. Действительно, все функции системы являются линейными, поэтому в силу того, что суперпозиция линейных функций есть линейная функция, замыкание этой системы принадлежит классу линейных функций, а
не зависит от этой системы. Действительно, все функции системы являются линейными, поэтому в силу того, что суперпозиция линейных функций есть линейная функция, замыкание этой системы принадлежит классу линейных функций, а  — функция не линейная. Поэтому
— функция не линейная. Поэтому  не зависит от данной системы функций.
не зависит от данной системы функций.
Пример 2: Рассмотрим функцию  и систему
и систему  :
:
x1 x2 



|
|
Дата добавления: 2017-01-13; Просмотров: 279; Нарушение авторских прав?; Мы поможем в написании вашей работы!