Геометрический метод нахождения всех минимальных ДНФ функции f

Утверждение о максимальных интервалах и тупиковых покрытиях.

Д/з.

Д/з.

Определение: Покрытием единиц булевой функции f называют набор допустимых интервалов, таких что каждая единица булевой функции принадлежит некоторому из интервалов.

Пример:

001 011

x₂x₃

101 111

x₁x₂

000 010 x1x2

100 110

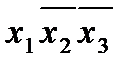
Рассмотрим четыре допустимых интервала, это есть покрытие. Действительно, каждый из интервалов является допустимым, каждый из интервалов состоит целиком из единиц функции f, и каждая единица функции f принадлежит некоторому интервалу (покрыта некоторым интервалом).

Утверждение: Каждое покрытие представляет булеву ф-цию.

Действительно, в силу того, что каждый интервал покрытия является допустимым, на нулевом наборе булевой функции значение каждой конъюнкции интервала равно 0. Если же рассматриваем единичный набор булевой функции (набор, на котором значение функции равно 1), то значение ДНФ, которая соответствует покрытию равна 1, т.к. значение конъюнкции, соответствующей набору, который покрывает данный набор равно 1.

ДНФ, которая соответствует покрытию, представляет булеву функцию.

Утверждение: Любой ДНФ, которая представляет f, соответствует покрытие.

Определение: Тупиковым покрытием называют покрытие, при удалении любого интервала из которого, оно перестает быть покрытием.

Пример: Рассмотренное в предыдущем примере покрытие является тупиковым. Действительно, если удалим интервал x₂ x ₃ , то вершина 011 не будет принадлежать ни одному из оставшихся интервалов. Если удалим x ₁ x ₃, то тогда не будет покрыта вершина 101, если удалим x ₁ 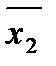, то не будет покрыта вершина 100, если удалим x ₁ x ₂ , то не будет покрыта вершина 110. Добавим к рассмотренномупокрытию x ₁ x ₂, тогда имеем не тупиковое покрытие. Действительно, можно удалить интервал x ₁ x ₂ и все равно получим покрытие.

Утверждение 1: Любая минимальная ДНФ может состоять только из максимальных интервалов.

Утверждение 2: Любая минимальная ДНФ - есть тупиковое покрытие.

Докажем утверждение 1:

Допустим противное, что некоторая минимальная ДНФ k ₁Ú k ₂Ú...Ú k _s содержит немаксимальный интервал k ₁ . Это означает, что из интервала k ₁ можно удалить множитель, так что полученный интервал k ₁^/ так же будет допустимым.

Заменим интервал k ₁ на k ₁^/ в начальной ДНФ функции f. Нетрудно видеть, что полученная ДНФ k ₁^/ Ú k ₂Ú...Ú k _s также представляет функцию f.

Действительно, в силу одного из предыдущих утверждений интервал k ₁ Í k ₁^/. Это означает, что любая единица, которая была покрыта интервалом k ₁, будет покрыта интервалом k ₁^/. Все остальные единицы были покрыты оставшимися интервалами. Они же покрыты интервалами (оставшимися) в полученной ДНФ. Таким образом, все единицы функции f покрыты полученными интервалами. И все интервалы данного набора являются допустимыми. Поэтому полученная ДНФ является покрытием и поэтому представляет функцию f. Но сложность полученной ДНФ меньше, чем сложность первоначальной, т. к. в интервале k ₁ был удален некоторый множитель.

Отсюда следует противоречие. Мы получили ДНФ, сложность которой меньше чем сложность первоначальной.

Пример: Рассмотрим булеву функцию x ₁ x ₃ Ú x ₂ x ₃ Ú x ₁ и рассмотрим покрытие соответствующее данной функции.

x₁x₃

x₂x₃

Действительно, это покрытие, но данное покрытие не можетсоответствовать минимальной ДНФ из-за того что интервалы x ₁ x ₃ и x ₁ не являются максимальными.

Действительно, из интервала x ₁ x ₃ можно удалить множитель x ₃ и получится допустимый интервал x ₁. И сложность ДНФ, которая так же является покрытием, уменьшится на 1.

Поэтому первоначальное покрытие не может быть минимальным. В данном примере минимальная ДНФ есть x ₁ Ú x ₂ x ₃. Д/з.

Докажем утверждение 2:

Любая минимальная ДНФ есть тупиковое покрытие.

Допустим противное, что есть минимальная ДНФ k ₁Ú k ₂Ú...Ú k _s, которая не является тупиковым покрытием. Это означает, что в ДНФ есть интервал k ₁ (для определенности), удаление которого все равно приведет к покрытию k ₂Ú...Ú k _s, т. е. полученное покрытие будет представлять булеву функцию, но сложность полученной ДНФ для данного покрытия меньше чем сложность первоначальной ДНФ на величину ранга удаленной конъюнкции. Поэтому первоначальная ДНФ не может является минимальной.

Из данных двух утверждений следует, что минимальная ДНФ содержится в множестве всевозможных тупиковых, состоящих из максимальных интервалов.

Замечание: Тупиковая ДНФ не обязательно является минимальной.

Например: x ₁ x ₃ Ú x ₂ x ₃ Ú x ₁ . Действительно, данные интервалы составляют тупиковое покрытие. Но данная ДНФ не является минимальной.

Данное утверждение не верно даже если предполагать, что тупиковая ДНФ состоит только из максимальных интервалов.

Пример:

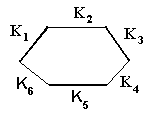
Максимальными интервалами являются 6 ребер: k ₁ , k ₂ , k ₃, k ₄, k ₅, k ₆. Они действительно являются максимальными, ни одно из ребер не содержится в допустимой грани. Допустимых граней здесь нет.

Не трудно видеть, что k ₁ , k ₂ , k ₄ , k ₅ является тупиковым покрытием. Действительно, все интервалы допустимы и максимальны, и при удалении любого интервала получаем не покрытие. Но данное тупиковое покрытие максимальными интервалами минимальным не является. В данном примере существует покрытие меньшей сложности, которое покрывает все вершины, а сложность этого покрытия меньше: k ₁, k ₃, k ₅,.

Ответ: Минимальные ДНФ следующие:

Таким образом, алгоритм нахождения минимальной ДНФ будет проводиться в два этапа: на первом найдем все максимальные интервалы функции f, а на втором — все тупиковые покрытия максимальными интервалами, и выделим из них покрытия минимальной сложности. Это и будут все минимальные ДНФ функции f.

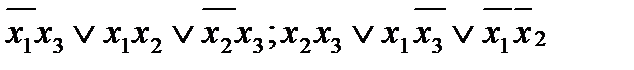
001 011

101 111

000 010

100 110

Первый этап:

Рассмотрим пример. В нем максимальные интервалы x ₁ и x ₂ . Действительно, x ₁ является допустимым, он состоит целиком из единиц функции f, удаление множителя x ₁ из данного интервала дает интервал константу 1. Это все вершины булевого куба. Вершина 000 единицей не является. Поэтому const 1 — весь булев куб допустимым интервалом не является. Поэтому интервал x ₁ является максимальным.

Интервал x ₂ так же является максимальным.

Второй этап:

Найдем все тупиковые покрытия. Получаем единственное покрытие, состоящее из всех максимальных интервалов. Действительно, интервал x ₂ обязательно должен принадлежать покрытию, т.к. только данный максимальный интервал покрывает вершину 011.

Интервал x ₁ также обязан принадлежать покрытию, т.к. только данный максимальный интервал покрывает вершину 100.

Таким образом, множество всех тупиковых покрытий максимальными интервалами состоит из единственного покрытия, которое и является единственным минимальным.

Поэтому получаем единственную минимальную ДНФ .

Рассмотрим функцию от трех переменных.

1 этап:

Находим максимальные интервалы данной функции. Их будет 4. Это четыре ребра: x ₁ 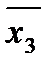, x ₁ x ₂, x ₂ x ₃ , x ₃ .

K₄

K₃

Действительно, данные интервалы являются допустимыми и при удалении любого множителя получается интервал грань, а допустимых граней для данной функции нет. Других максимальных интервалов для данной функции также не существует.

Первый этап завершен.

2 этап:

Найти все тупиковые покрытия.

; .

И других тупиковых покрытий нет.

Действительно, интервал обязан входить в любое покрытие, т.к. только он покрывает вершину 100. Интервал 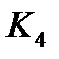обязан входить в любое покрытие, т.к. только он покрывает вершину 001. Остаются два интервала 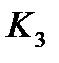; 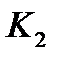, из которых достаточно взять только один интервал, чтобы покрыть вершину 111. Сложность тупиковых покрытий одинакова. Это и есть все минимальные ДНФ данной функции.

Ответ: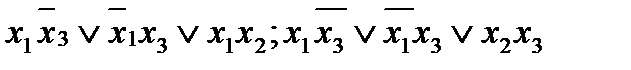

Дата добавления: 2017-01-13