Метод включения-исключения

Разное.

В следующих пяти задачах следует посчитать число возможных комби­наций, получающихся при бросании пяти различных (одинаковых) играль­ных кубиков.

1. Комбинации 3+2, т.е. на некоторых двух и оставшихся трех костях одинаковые цифры. Пример:11144 или 33333

2. Комбинации: имеется хотя бы четыре одинаковые цифры. 44443 или 44444.

3. Комбинации: 2+2, то есть на некоторых двух парах костей одна цифра. 11224 или 11222 или 11113 или 11111.

4. Комбинации: на всех костях различные цифры 134.56

5. Комбинации, когда хотя бы на трех костях одна цифра. 11123 или 11114 или 11111.

6. Имеется колода карт 4-рех мастей по 9 карт каждой масти. Из выборов 7-ми карт найти число комбинаций, когда имеются все масти.

7. Составляют шестизначные числа из цифр 1,2,3. Найти число чисел, в которых участвуют все цифры. -.-

8. Найти число шестизначных чисел из цифр 1,2,3 с четной суммой цифр. Все цифры присутствуют в числе.

9. Найти число вершин, ребер, граней, кубов четырехмерного булевого куба.

10. Найти число счастливых четырехзначных номеров с суммой цифр не больше 18.

11. Найти ошибку в решении следующей задачи:

Имеется колода карт4-ех мастей по 9-ть карт каждой масти. Берут шесть карт. Найти число комбинаций, в которых имеются все масти, причем, в некоторые две масти попало по две карты в каждую, а в оставшиеся масти по одной.

Решение. Выбираем первую масть и две карты, которые попали в эту масть: имеем 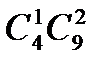способов. Затем выбираем еще одну масть и две карты в ней таким же числом способов. После этого в оставших­ся двух мастях выбираем по одной карте: 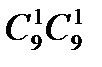возможностей. Теперь перемножаем все числа и получаем ответ: .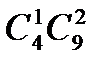

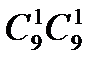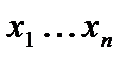Пусть имеется множество элементов и пусть имеется множество свойств , которыми элементы могут обладать или нет. Пусть 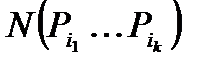— число элементов, обладающих свойствами . Пусть 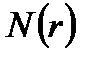обозначаетчислоэлементов, обладающих ровно свойствами.

Теорема. =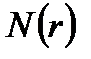

Доказательство.

1. Рассмотрим элемент обладающий ровно свойствами. Такой элемент войдет в 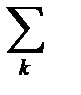только при и в сумме 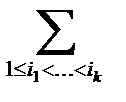будетсчитаться единственный раз. Поэтому элементы, обладающиеровно свойствами, будут входить в сумму по одному разу.

2. Рассмотрим элемент обладающий ровно 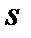свойствами, .Тогда в 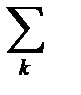они будут входить при а в 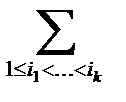они войдут раз. Тогда общее число вхождений такого элемента есть

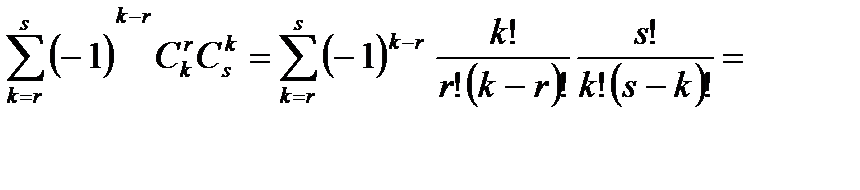
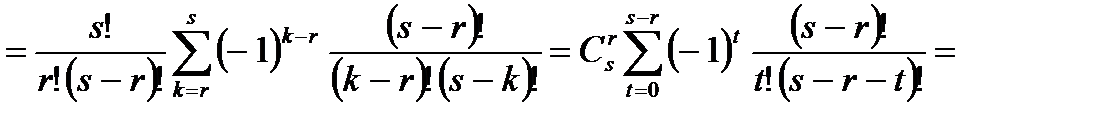
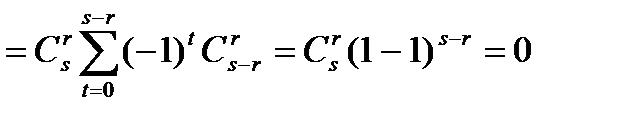
Таким образом, из 1 и 2 следует требуемое свойство.

Пример 1. Подсчитать число перестановок, оставляющих на месте ровно элементов.

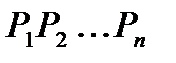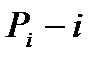Решение. Вводим множество всех перестановок элементов . Вводим n свойств : -тый элемент при перестановке 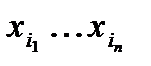остается на месте. Тогда число перестановок, оставляющих на месте ровно эле­ментов, есть:

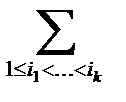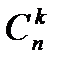где N() — число перестановок, оставляющих на ме­сте -ый, -ой,…, -ый элементы, и это число есть очевидно, (n-k)!, а число слагаемых в сумме есть . Поэтому искомое число есть

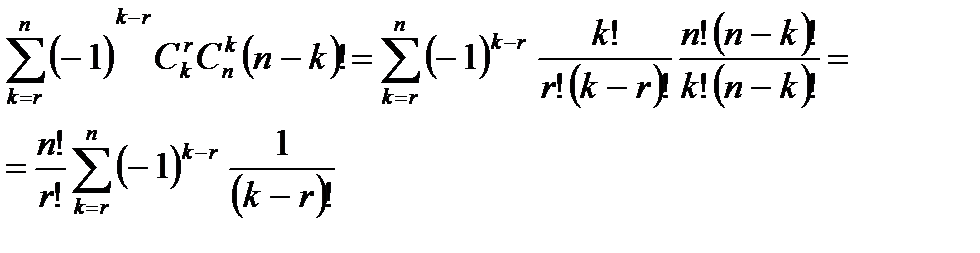
Здесь

И при больших 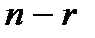получим ассимтотическую формулу

Пример 2. Найти число чисел взаимно простых с данным . Обозначим это число через 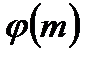(так называемая функция Эйлера).

Решение. Введем множество натуральных чисел 1, 2,..., т и введем свойства 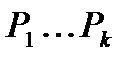, где 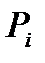означает, что число делится на про­стое число 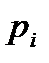. Тогда числа взаимно простые с т есть числа, которые не обладают ни одним из свойств 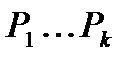, т.е. обла­дают 0 свойствами, и поэтому искомое число есть

где есть число чисел, делящихсяна 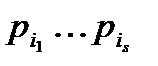, и поэтому это числа, представленные в виде

где множитель h изменяется 1,2, Поэтому =

и тогда = =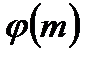

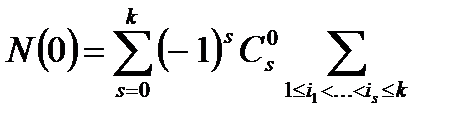
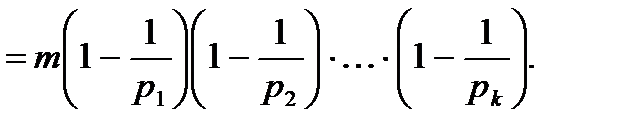
Пример 3. Найти число способов раскладки m различных шаров по n различным урнам, при которых ровно урн пусты.

Решение. Введем множество различных раскладок m различных ша­ров по n различным урнам, т.е. упорядоченных наборов m эле­ментов из множества {1,2,..., n } n- элементов с возможными повторениями. Введем свойства раскладок 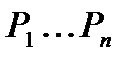. 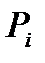— i -ая урна пуста. Тогда искомое число есть 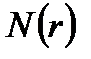— ровно 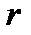урн пусты.

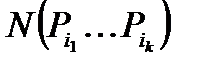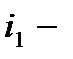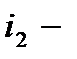— число раскладок, при которых ая, ая, ая урны пусты и это число, как нетрудно видеть, есть 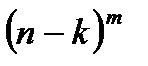.Поэтому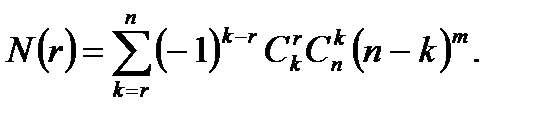

Дата добавления: 2017-01-13