
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры подгрупп
|
|
|
|
1. Группа вращений правильного треугольника:
1 2 3 – тождественная перестановка;
2 3 1 – вращение по часовой стрелке;
3 1 2 – вращение против часовой стрелки.
32
Нетрудно проверить, что произведение любых двух перестановок нашей группы есть перестановка нашей группы, есть перестановка нашей группы.
Данная группа является подгруппой группы всех 3!=6 перестановок трех элементов.
2. Группа всех вращений тетраэдра:
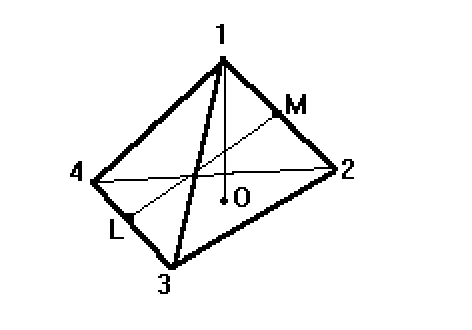 1) Вращения относительно высоты 10 тетраэдра на 120
1) Вращения относительно высоты 10 тетраэдра на 120  по часовой и против часовой стрелки:
по часовой и против часовой стрелки:
(10) 1 3 4 2 1 4 2 3
(2) 4 2 1 3 3 2 4 1
(3) 2 4 3 1 4 1 3 2
(4) 3 1 2 4 2 3 1 4
2)Вращения относительно осей LM проходящих через середины противоположных сторон на 180 
2 1 4 3 4 3 2 1 3 4 1 2.
3)Тождественная - 1 2 3 4.
Всего 12 перестановок. Эта группа является подгруппой группы всех 4!=24 перестановок четырех элементов. В обоих примерах порядок подгруппы (т.е. число элементов в ней) делит порядок группы.
Имеет место
Теорема Лагранжа. Порядок подгруппы делит порядок группы.
Доказательство. Пусть имеется группа G и ее подгруппа H. На множестве элементов группы зададим следующее отношение: скажем, что два элемента a и b группы эквивалентны, если найдется элемент 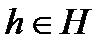 что
что 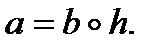 . Это отношение обладает тремя свойствами:
. Это отношение обладает тремя свойствами:
- Оно рефлексивно, т.е.
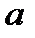 ~ a для любого а. Это верно, так как
~ a для любого а. Это верно, так как  , где
, где 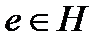 (Н -подгруппа).
(Н -подгруппа). - Оно симметрично, т.е. если а~b, то b~a. Это верно, так как из первой эквивалентности следует, что
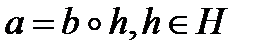 и поэтому
и поэтому  (
( так как Н подгруппа, здесь мы так же использовали ассоциативность умножения в группе).
так как Н подгруппа, здесь мы так же использовали ассоциативность умножения в группе). - Оно транзитивно, т. е. если a ~ b и b ~ c, то a ~ c. Этоверно, так как из первой эквивалентности следует, что
 из второй следует
из второй следует 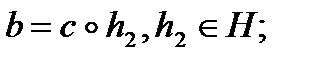 тогда
тогда  так как Н подгруппа.
так как Н подгруппа.
Тогда нетрудно видеть, что данное отношение эквивалентности разобьет все множество G на левые классы эквивалентных непересекающихся множеств, называемых левыми смежными классами группы G по подгруппе Н. (В одном классе эквивалентные между собой элементы, в разных неэквивалентные).
|
|
|
Причем в каждом классе содержится ровно 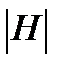 элементов. (Класс, содержащий некоторый элемент а, содержит элементы
элементов. (Класс, содержащий некоторый элемент а, содержит элементы  где h пробегает группу Н, а их ровно
где h пробегает группу Н, а их ровно 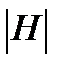 ). Классы не пересекаются, и поэтому порядок подгруппы Н делит порядок группы G.
). Классы не пересекаются, и поэтому порядок подгруппы Н делит порядок группы G.
Данное утверждение можно доказать также используя разложение на правые классы смежности группы G по подгруппе Н.
Пример. Группа вращений треугольника Н является подгруппой группы G всех перестановок трех элементов.
Н: 1 2 3 2 3 1 3 1 2
G: 1 2 3 1 3 2 3 2 1 2 1 3 2 3 1 3 1 2
Разложение на классы эквивалентных элементов имеет вид:
1 2 3, 2 3 1, 3 2 1 2 1 3, 1 3 2, 3 2 1.
Первый класс есть (1 2 3)  , второй (1 3 2)
, второй (1 3 2) 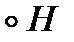 .
.
Теперь займемся следующей задачей:
- Имеется множество объектов Х:слова длинны п в алфавите
 .
. - Имеется группа перестановок G в алфавите букв длинны п. Два слова
 назовем эквивалентными
назовем эквивалентными  , если для некоторой перестановки
, если для некоторой перестановки  , имеем: слово
, имеем: слово  совпадает со словом
совпадает со словом  .
.
Утверждение 7. Введенное отношение является отношением эквивалентности.
1. Оно симметрично. Если  , то
, то  =
=  , тогда
, тогда 
 .
.
2. Оно рефлексивно  , так как
, так как 
3. Оно транзитивно: если  ,
,  то
то  =
=  ,
,  =
= 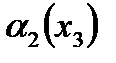 ,
,
тогда 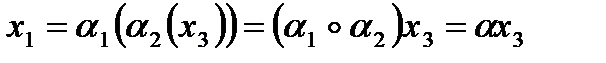 , где
, где 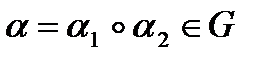 (здесь мы также использовали ассоциативность преобразования букв слова).
(здесь мы также использовали ассоциативность преобразования букв слова).
Таким образом, данное отношение разбивает множество слов на классы эквивалентных слов или, как будем называть в дальнейшем, на орбиты. Наша основная цель - найти число орбит.
Для некоторого слова х рассмотрим множество перестановок N(x):  ,
,
т.е. это перестановки, которые оставляют на месте данный объект. (Например, для слова 010 такой перестановкой служит слово 321, когда первая и третья буквы слова меняются местами, а также тождественная 123).
Утверждение 8. Множество N(x) является группой.
Действительно это верно, так как, если  принадлежат N, то
принадлежат N, то 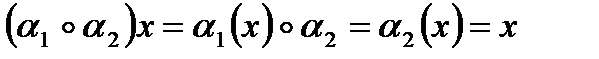 . В силу Утверждения 7. и следует требуемое.
. В силу Утверждения 7. и следует требуемое.
|
|
|
Теперь сформулируем основное утверждение параграфа.
Лемма 1. Бернсайда. Число орбит элементов множества Х относительно группы перестановок G равно  . (Здесь п(а) число слов х,
. (Здесь п(а) число слов х,
которые не изменяются при перестановке а.)
Для доказательства рассмотрим таблицу: ее строки — это элементы группы G, а столбцы — это слова х;на пересечении строки а и столбца х ставим 1, если а(х) = х..
Тогда число единиц в таблице можно получить, суммируя их по строкам или, суммируя их по столбцам, т.е.
 . (1)
. (1)
Наша цель — преобразовать сумму в правой части к нужному виду. Сумму в правой части удобно посчитать, разбив элементы на орбиты

Рассмотрим некоторую орбиту О и два элемента 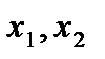 из этой орбиты. Покажем справедливость утверждений.
из этой орбиты. Покажем справедливость утверждений.
Утверждение 9. 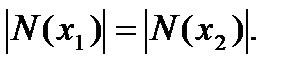
Утверждение 10. Число слов в орбите О равно  (в силу предыдущего утверждения, число слов в орбите не зависит от выбора представителя орбиты.)
(в силу предыдущего утверждения, число слов в орбите не зависит от выбора представителя орбиты.)
Доказательство. (Утверждение 9.)
 означает, что
означает, что 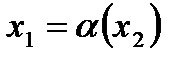 при некоторой перестановке
при некоторой перестановке  .
.  - это перестановки
- это перестановки 
Рассмотрим перестановки  (N обозначает N(
(N обозначает N( )). Нетрудно видеть, что
)). Нетрудно видеть, что 
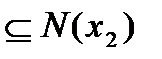 Действительно,
Действительно,
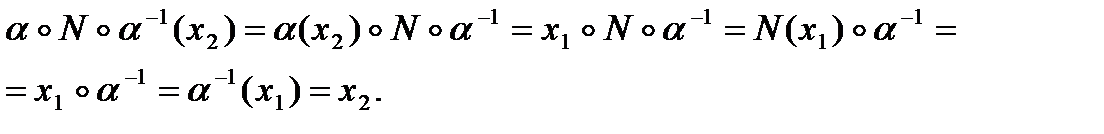
Причем, если  , то
, то 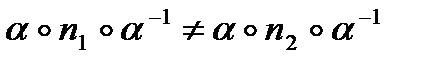 , поэтому
, поэтому 
В силу эквивалентностислов  следует и обратное неравенство
следует и обратное неравенство
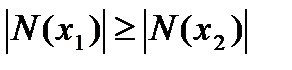 ,что и дает требуемое.
,что и дает требуемое.
Доказательство. (Утверждение10. )
Пусть х некоторый элемент орбиты О. Чтобы найти число элементов в орбите О, нужно к элементу х применить все перестановки группы G, и тогда все полученные различные элементы и будет орбита О.
Разобьем все перестановки из G на правые классы смежности по подгруппе N(х). Покажем, что для любых перестановок 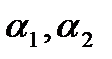 из одного класса будем иметь
из одного класса будем иметь 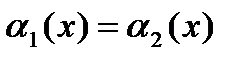 , а из разных классов
, а из разных классов 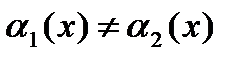 . Это и означает, что число элементов в орбите равно числу классов смежности группы G по подгруппе N(х), т.е. числу
. Это и означает, что число элементов в орбите равно числу классов смежности группы G по подгруппе N(х), т.е. числу  . Действительно, если
. Действительно, если 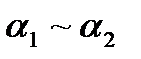 , то
, то  , где
, где  N(х}. Тогда
N(х}. Тогда
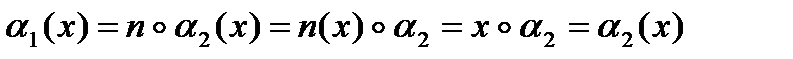
Пусть теперь  неэквивалентна
неэквивалентна 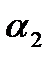 . Покажем, что
. Покажем, что 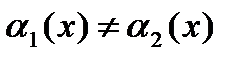
Действительно, если это не так, т.е. 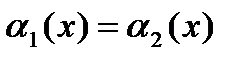 , то
, то
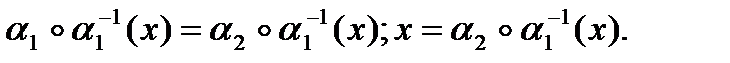
Таким образом  , т.е.
, т.е. 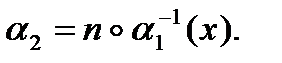 перестановки эквивалентны. Противоречие. Утверждение 10 доказано.
перестановки эквивалентны. Противоречие. Утверждение 10 доказано.
Теперьможно доказать Лемму Бернсайда. Доказательство. Имеем равенство (1).
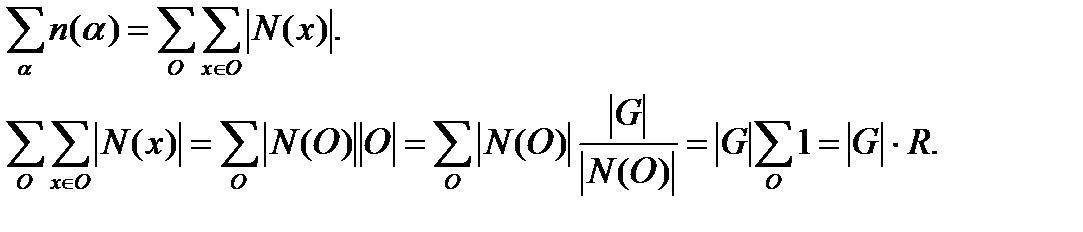
Здесь 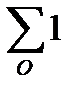 — есть не что иное, как число орбит, обозначено какR,
— есть не что иное, как число орбит, обозначено какR,
число N(х) не зависит от представителя 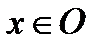 , обозначим его —
, обозначим его —
|
|
|
N(0). Тогда, деля левую часть равенства на 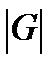 получаем требуемую формулу.
получаем требуемую формулу.
Осталось показать, как вычислять п(а) — число слов в алфавите из s символов, которые не изменяются при перестановке а. Нетрудно показать, что любую перестановку можно представить в виде произведения циклов.
Например, 21453 есть произведение 12  345, цикл 345 означает, что третья буква переходит на четвертое место, четвертая на пятое, а пятая на третье, т.е. буквы третья, четвертая и пятая сдвигаются по циклу, а все остальные остаются на месте. Цикл 12 определяется аналогично. Тогда слова, которые не изменяются при перестановке 21453 — это слова, у которых на первом и втором месте стоит одна и та же буква, и на третьем, четвертом и пятом месте стоит одна и та же буква. В данном случае число слов равно
345, цикл 345 означает, что третья буква переходит на четвертое место, четвертая на пятое, а пятая на третье, т.е. буквы третья, четвертая и пятая сдвигаются по циклу, а все остальные остаются на месте. Цикл 12 определяется аналогично. Тогда слова, которые не изменяются при перестановке 21453 — это слова, у которых на первом и втором месте стоит одна и та же буква, и на третьем, четвертом и пятом месте стоит одна и та же буква. В данном случае число слов равно 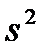 . В общем случае, если перестановка а раскладывается в k циклов, то
. В общем случае, если перестановка а раскладывается в k циклов, то 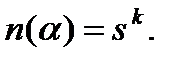
Пример. Каким числом способов можно раскрасить вершины тетраэдра
в три цвета. Два тетраэдра различно раскрашены,если их нельзя перевести
друг в друга вращениями в пространстве.
Решение. Рассмотрим множество объектов Х — слова длины 4 в алфавите из трех элементов. Это все окрашенные тетраэдры, включая эквивалентные (т.е. зафиксировали тетраэдр и всевозможными способами раскрасили его вершины, при этом некоторые раскраски естественно оказываются эквивалентными, т.е. одну из другой можно получить поворотами в пространстве).
Наша задача посчитать число неэквивалентных раскрасок. Рассмотрим группу вращений тетраэдра Н относительно которой и рассматриваем неэквивалентность раскрасок. Тогда число различных раскрашенных тетраэдров есть число орбит Х относительно Н. Найдем числа 
1. 1342 = 1  234, п =
234, п =  = 9 и таких перестановок в первой группе 8.
= 9 и таких перестановок в первой группе 8.
2. 2143 == 12  34; п =
34; п =  = 9 и таких перестановок три.
= 9 и таких перестановок три.
3. 1234 =1 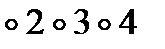 ; п = 34 = 64.
; п = 34 = 64.
По лемме Бернсайда искомое число есть 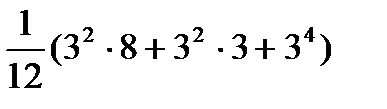 =15. Здесь 12 число элементов в группе вращений тетраэдра.
=15. Здесь 12 число элементов в группе вращений тетраэдра.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 720; Нарушение авторских прав?; Мы поможем в написании вашей работы!