Элементы теории конечных автоматов

Утвердение

Оценка сложности функций n переменных.

Сложность любой двочной функции не более чем n перменных лежит в пределах:

при некоторых положительных константах и .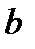

Доказательство:

Покажем справедливость верхней оценки. Рассмотрим любую двоичную функцию и разложим данную функцию по первым 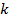переменным. Справедлива формула :

(*)

.

По данной формуле построим схему, которая будет вычислять данную . Реализуем схему вычисления следующим образом:

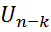
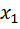
Рассмотрим дешифрование порядка 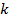, где . Скобками 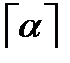обозначают минимальное натуральное число превосходящее действительное число .

(логарифм по основанию 2). Очевидны оценки:

Схема нарисована согласно формуле 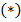, т.е. на остаточные входы дешифратора подаются соответствующие функции от переменных, которые получаются универсальным многополюсником.

Т.о. сложность построенной схемы:

Покажем, что каждое слагаемое есть

1)

т.к. 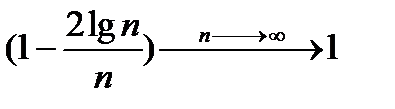, поэтому ограничена;

2) т.к. , , поэтому ограничена;

3) .

Требуемое доказано. Оценим сложность функции снизу, применяя мощностной метод.

Пусть число функциональных элементов в схеме 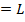. Обозначим символом число схем с входами, число элементов в которых 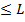. Покажем, что число таких схем удовлетворяет оценке: .

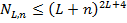Действительно, элементы схемы можно разбить на группы с числом конъюнкций 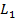, дизъюнкций и отрицаний 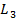не более чем способами (единица в формуле появляется в силу того, что некоторые группы могут быть пустыми). Теперь перечислим всевозможные соединения элементов. Каждый элемент в схеме имеет не более 2-х входов. Каждый вход можно соединить не более чем с выходами других элементов, либо с входами схемы.

Поэтому общее число соединений одного элемента не больше , а т.к. элементов не превосходит , то общее число соединений элементов не больше чем .

Осталось назначить общий выход схемы, это можно сделать способами (в схеме элементов и выходов). Таким образом, общее число схем не превосходит 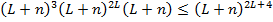, т.к. число переменных в схеме не менее 1.

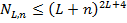
Что и требовалось доказать.

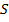В качестве возьмем сложность , т.е. минимальное число элементов для реализации всех функций от переменных выполняется: 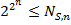. Т.е. число различным схем сложности 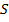не менее общего числа функций от переменных. В противном случае некоторая функция от переменных не могла быть реализована схемой сложности .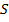

Используя оценку получаем . Прологарифмируем данное неравенство: . Используя полученную ранее верхнюю оценку сложности для функции Шенона легко показать необходимую оценку.

Справедливы следующие элементарные арифметические выкладки:

по ранее полученной оценке Шеноновская сложность двоичных функций от переменных в асимптотике:

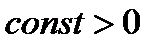, поэтому 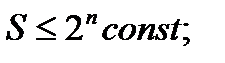, 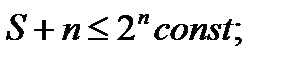поэтому

,

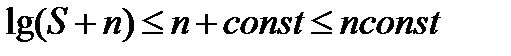тогда ;

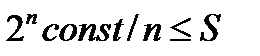
при некоторой положительной константе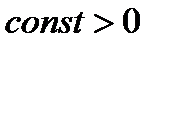

Утверждение.(Лупанов О.Б)

Справедлива точная асимптотика функции сложности:

, .

Определение. Рассмотрим два конечных множества и . Будем называть их входным и выходным алфавитами соответственно. Элементы алфавитов будем называть буквами.

Все бесконечные последовательности букв алфавита будем обозначать и называть бесконечными словами. Символом 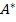будем обозначать всевозможные конечные слова в алфавите . Слова длины 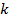в алфавите будем обозначать – декартово произведение множества на себя 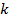раз. Скажем, что слово 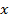является началом слова или приставкой, если для некоторого слова . Длину конечного слова 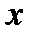, т.е. число его букв, будем обозначать как .

Пример. – начало слова 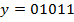, где .

Напоминаем некоторые введенные ранее понятия.

Пусть – конечное множество. Отношением на данном множестве будем называть любое подмножество его декартового произведения . Рассмотрим декартово произведение на себя: . Т.е. это множество всевозможных слов из двух букв в алфавите . Отношением эквивалентности 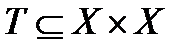называется подмножество декартового произведения, которое удовлетворяет следующих трем свойствам:

4. Рефлексивность. .

5. Симметричность. .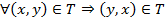

6. Транзитивность. .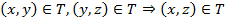

Дата добавления: 2017-01-13