Денежные лотереи и отношение к риску

Существование функции ожидаемой полезности

Следствие аксиомы независимости.

Если предпочтения, определенные на , удовлетворяют аксиоме независимости и лотереи L,L` таковы, что L L`, α,β ∊ (0,1), то:

αL + (1-α)L` βL + (1-β)L` тогда и только тогда, когда α β;

αL + (1-α)L` 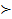βL + (1-β)L` тогда и только тогда, когда α > β;

Функция полезности фон Неймана-Моргенштерна может подвергаться лишь монотонным преобразованиям вида при a>0, т.е. аффинным преобразованиям[1], изменяющим исходную точку и/или масштаб вертикальной оси, но не влияющим на «форму» функции. Поэтому данная функция является кардиналистской: ее нельзя считать лишь неким индексом полезности — ее конкретные значения имеют вполне определенный смысл. Соответственно, конкретный смысл приобретают и рассуждения о возрастающей, неизменной и убывающей предельных полезностях.

Лотереи, исходами которых являются не потребительские наборы, а денежные суммы, называются денежными лотереями. Сумму денег удобно рассматривать как непрерывную переменную, характеризуя ее посредством функции распределения. Такую лотерею можно описать посредством функции распределения F(x) = prob(х̅ x), т.е. как вероятность того, что случайная величина х̅ примет значение меньшее или равное х. В этом случае функция ожидаемой полезности примет вид U(F) = . Функцию U, определяемую на лотереях, мы называем функцией полезности фон Неймана –Моргенштерна, а функцию u(x), зависящую от суммы денег (богатства), принято называть элементарной функцией полезности или функцией полезности Бернулли. Далее будем считать, что u(x) – непрерывная, возрастающая функция.

Классификация агентов по степени принятия риска:

1) Будем говорить, что индивид не склонен к риску, если любая лотерея F∊ для него не лучше ожидаемого выигрыша этой лотереи, полученного с определенностью. Если индивидуум строго предпочитает ожидаемый выигрыш самой лотерее, то говорят, что он строго не склонен к риску или он является рискофобом. Если предпочтения индивида представимы с помощью функции ожидаемой полезности, то несклонность к риску означает, что любой функции распределения выполняется соотношение U(F) = u(.

Вогнутая функция полезности индивида, не склонного к риску

Форму функции полезности можно объяснить интуитивно принимаемой предпосылкой об убывании предельной полезности от каждой дополнительной единицы «призовых» денег (т.е. богатства) по мере укрупнения выигрыша. Бросок монеты в 1000 руб. золотом сулит вам сравнительно небольшой прирост полезности при выигрыше, но зато сильное ее снижение при проигрыше. Напротив, ставка в 5 руб. в этом смысле несущественна: прирост полезности при выигрыше и ее уменьшение при проигрыше практически уравновешивают друг друга.

2)Будем говорить, что индивидуум нейтрален к риску, если он всегда безразличен между лотерей и ее ожидаемой величиной, полученной с определенностью. Нейтральность к риску означает равенство ожидаемой полезности и полезности от ожидаемого выигрыша U(F) = = u( для любой F, что соответствует линейности u(x).

3)Будем говорить, что индивидуум склонен к риску, если он предпочитает любую лотерею F ее ожидаемому выигрышу, полученному с определенностью. Если потребитель строго предпочитает лотерею ее ожидаемой величине, то говорят, что он является рискофилом. Если предпочтения индивидуума представимы с помощью функции ожидаемой полезности, то склонность к риску означает, что для любой функции распределения F() выполняется соотношение U(F) = u(.

Дата добавления: 2017-01-13