Из уравнений (1.51) и (1.52) следует, что в состоянии равновесия

Если в системе протекает обратимая химическая реакция

Химическое равновесие. Расчет констант равновесия обратимых химических реакций

При протекании обратимых химических реакций через некоторое время в системах устанавливается равновесное состояние – химическое равновесие.

aA + bB ↔ eE + dD, (1.48)

то при химическом равновесии скорости прямой и обратной реакций равны, а концентрации всех реагирующих веществ перестают меняться и остаются постоянными во времени при неизменных внешних условиях. Равновесие может быть достигнуто при протекании процесса в зависимости от состава системы, как в прямом, так и в обратном направлении (как слева направо, так и справа налево).

При протекании реакции в изобарно-изотермических условиях (P = const, T = const) для определения направленности процесса и состояния равновесия используется величина изменения свободной энергии Гиббса ΔG (изобарно-изотермического потенциала) для данной химической реакции. Часть изобарно-изотермического потенциала, приходящегося на один моль вещества, участвующего в реакции, называется химическим потенциалом данного вещества (μ_i) и выражается следующей производной:

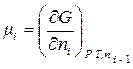. (1.49)

В состоянии равновесия свободная энергия Гиббса достигает своего минимального значения и не изменяется. Условие равновесия химической реакции: dG = 0. Так как dG = Σμ_i· dn_i, то в состоянии равновесия сумма химических потенциалов всех составляющих системы, умноженных на соответствующие стехиометрические коэффициенты, равна нулю:

Σμ_i· dn_i = 0, или (1.50)

eµ_E + dµ_D – aµ_A – bµ_B = 0. (1.51)

Химический потенциал каждого участника химической реакции является функцией активности a_i этого компонента:

µ_I = µ_I^o + RT lna_i, (1.52)

где µ_I^o – стандартный химический потенциал (при а_i = 1);

a_i – термодинамическая активность – величина, связанная в реальных системах с другими термодинамическим величинами так, как с ними связана концентрация в идеальных системах (a_i = γ_i· c_i, где γ_i – коэффициент термодинамической активности, зависящий от природы веществ, их концентрации и внешних условий).

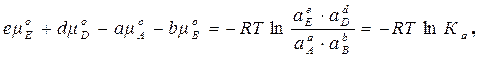(1.53)

где K_a – константа равновесия химической реакции, выраженная через равновесные активности веществ, участвующих в реакции:

(1.54)

Для идеальных систем константа равновесия может быть выражена через равновесные молярные концентрации с_i:

(1.55)

через равновесные парциальные давления P_i:

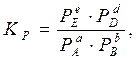(1.56)

через равновесные мольные доли реагентов:

(1.57)

Уравнения (1.54) – (1.57) отражают закон действующих масс для обратимых химических реакций, который читается следующим образом: при постоянных температуре и давлении отношение произведения равновесных концентраций (парциальных давлений) продуктов реакции к произведению равновесных концентраций (парциальных давлений) исходных веществ в степенях, равных соответствующим стехиометрическим коэффициентам, есть величина постоянная.

Чем выше константа равновесия, тем более глубоко протекает прямая реакция до наступления состояния равновесия.

Для идеальных газов P_i = c_i RT и P_i = N_i P, где P – общее давление, поэтому представленные константы равновесия связаны следующим образом:

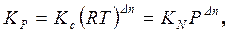(1.58)

где Δn – изменение числа молей газообразных участников реакции.

Например, если все компоненты реакции (1.48) находятся в газовой фазе, то

Δn = (e + d) – (a + b). (1.59)

Для химических реакций, проходящих в изобарно-изотермических условиях, изменение энергии Гиббса при переходе системы из исходного неравновесного состояния в равновесное (химическое сродство) можно рассчитать по уравнению изотермы Вант-Гоффа:

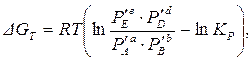(1.60)

где 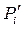– неравновесные парциальные давления (в исходном состоянии) веществ, участвующих в реакции.

Рассчитанное по уравнению (1.60) значение ΔG_T позволяет определить направление процесса: если ΔG_T < 0, то самопроизвольно идет прямая реакция, если ΔG_T > 0, то при данных парциальных давлениях компонентов самопроизвольно будет идти обратная химическая реакция. Если ΔG_T = 0, то при данных 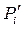система находится в состоянии равновесия.

Если в исходном состоянии парциальные давления каждого реагента равны 1 ( = 1), то есть все вещества вступают в реакцию в своих стандартных состояниях, то на основании уравнения (1.60) может быть получено уравнение для расчета стандартной энергии Гиббса (стандартного химического сродства):

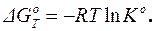(1.61)

Уравнение (1.61) может быть применено для расчета стандартной константы равновесия:

(1.62)

Методы расчета стандартных изменений энергии Гиббса при различных температурах (ΔG^o_T) приведены в главе 1.5.3.

Согласно принципу Ле Шателье, если на систему, находящуюся в равновесии, оказать внешнее воздействие, то равновесие смещается таким образом, чтобы снизить эффект этого воздействия. А именно, повышение давления смещает равновесие обратимой химической реакции в сторону уменьшения объема (то есть в сторону уменьшения количества молей газа). Повышение температуры сдвигает равновесие в сторону реакции, протекающей с поглощением теплоты.

Количественно зависимость константы равновесия от температуры описывается для процесса, протекающего при постоянном давлении, уравнением изобары Вант-Гоффа:

. (1.63)

Анализ этого дифференциального уравнения показывает, что для эндотермических реакций (ΔH^о > 0) c увеличением температуры константа равновесия увеличивается (равновесие смещается в сторону продуктов реакции), а для экзотермических реакций (ΔH^о < 0) с увеличением температуры константа равновесия уменьшается (равновесие смещается в сторону исходных веществ). Таким образом, эндотермические реакции целесообразно проводить при более высоких температурах, а для экзотермических процессов увеличению выхода продуктов реакции в равновесном состоянии будет способствовать понижение температуры.

После определенного интегрирования уравнения (1.63) в пределах от 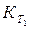до и от T₁ до T₂, принимая, что в данном температурном интервале тепловой эффект (изменение энтальпии ΔH^o) не зависит от температуры, получим уравнение:

, (1.64)

которое позволяет по константам равновесия при двух температурах рассчитать тепловой эффект реакции или по известным величинам теплового эффекта и константе равновесия при одной температуре найти константу равновесия при другой температуре.

При определении оптимальных условий химических реакций необходимо учитывать не только термодинамические факторы, но и кинетические, технологические и экономические возможности процессов.

П р и м е р 1.17. Для химической реакции, проходящей в газовой фазе при Т = 1000 К:

4 HCl + O₂ ↔ 2 H₂O + 2 Cl₂

рассчитать константы равновесия К_Р и К_С, если равновесные парциальные давления (Н/м² ) при температуре реакции составили:

P_HCl =1,553·10⁴; 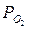= 2,210·10⁴; 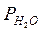= = 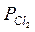3,185·10⁴.

Р е ш е н и е

Для расчета К_р подставим известные равновесные парциальные давления реагирующих веществ в выражение закона действующих масс (1.56), записанного для данной химической реакции:

Из соотношений (1.58) выражаем константу равновесия К_С:

∆ n находим по формуле (1.59):

∆ n = (2 + 2) – (4 + 1) = –1,

тогда

м³/моль

П р и м е р 1.18. Определить константу равновесия при Т = 298 К реакции:

Al₂O₃ + 3 SO₃ = Al₂(SO₄)₃

корунд газ кр.

Таблица 1.11

Дата добавления: 2017-01-14