Рекомендации к выполнению анализа спектральной плотности

Задание

Определение функций изображения по Лапласу и спектральной плотности одиночного импульса

При выполнении анализа указанного вида выполняются следующие задания:

a) используя свойства преобразования Лапласа, для заданного одиночного импульса вывести выражение для изображения по Лапласу;

b) выполнив в полученном выражении замену , получить комплексное выражение для спектральной плотности . Довести выражение спектральной плотности до показательной формы;

c) получить выражение для амплитудной спектральной характеристики 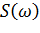– выражение модуля спектральной плотности;

d) получить выражение для фазовой спектральной характеристики 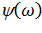– выражение аргумента спектральной плотности;

e) построить диаграммы амплитудного 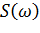и фазового 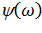спектра;

f) по диаграмме амплитудного спектра определить по пяти процентному критерию верхнюю граничную частоту спектра .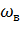

При выполнении пункта a) настоящего раздела 2 – при получении функции изображения по Лапласу S(p) – врамкахнастоящей работыучащиеся должны попрактиковаться в использовании свойств прямого преобразования Лапласа (таблица 2.1) и известных (табличных) изображений типовых оригиналов (таблица 2.2).

В вариантах заданий курсовой работы встречаются следующие разновидности импульсных сигналов (оригиналов):

- сигналы, содержащие интервалы с постоянными значениями и точки разрыва первого рода, но не содержащие интервалы с линейно-меняющимися функциями (рисунок Рисунок 2.1);

Таблица 2.1 – Свойства прямого преобразования Лапласа

Название свойства	Аналитическое выражение	Примечание
1. Линейности		константа, изображение оригинала , .
2. Смещение функции времени (теорема запаздывания)
3. Дифференцирование функции времени (свойство производной)		, .
	, .
4. Интегрирование функции времени (свойство первообразной)		.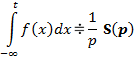

Таблица 2.2 – Спектральные характеристики типовых измерительных сигналов

Оригинал	Диаграмма функции оригинала	Функция оригинала	Изображение
Единичная ступенчатая функция (функция Хевисайда)
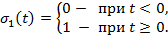
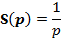
Единичная импульсная функция (дельта-функция)

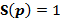
Рисунок 2.1 – Импульс, который возможно представить комбинацией ступенчатых функций

- сигналы, содержащие интервалы с линейно-меняющимися функциями (рисунок Рисунок 2.2). Интервалы с постоянными значениями и точками разрыва они могут либо содержать (рисунок Рисунок 2.2,а), либо не содержать (рисунок Рисунок 2.2,б).

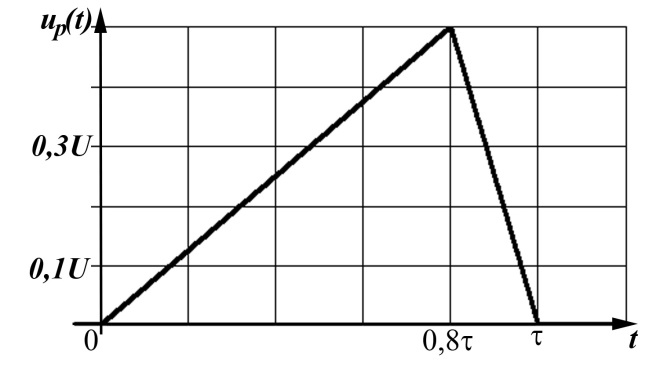а)

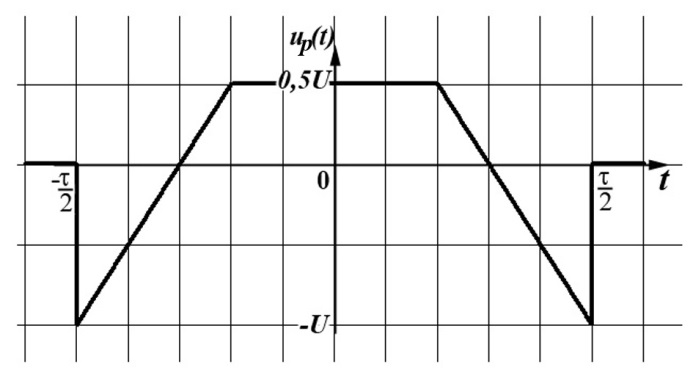б)

Рисунок 2.2 – Импульсы, содержащие наклонные отрезки

2.2.1 Функции изображений по Лапласу и по Фурье импульса, представляемого комбинацией ступенчатых функций (рисунок Рисунок 2.1)

	(3.1)
	(3.2)

2.2.2 Функции изображений по Лапласу и по Фурье импульса, представляемого комбинацией наклонных отрезков, без точек разрыва (рисунок Рисунок 2.2,а)

	(3.3)
	(3.4)

2.2.3 Функции изображений по Лапласу и по Фурье импульса, представляемого комбинацией наклонных отрезков, без точек разрыва (рисунок Рисунок 2.2,б)

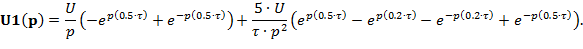
	(3.5)
	(3.6)

Дата добавления: 2017-01-14