
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тепловой изоляцией называют любое покрытие, способствующее уменьшению теплового потока через данную поверхность. 1 страница
|
|
|
|
Коэффициент теплопередачи равен количеству теплоты, передаваемой от одной среды к другой через единицу поверхности стенки в единицу времени при разности температур сред в один градус.
Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи. Для однослойной стенки
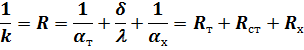
| (6) |
откуда следует, что полное термическое сопротивление равно сумме частных, причем
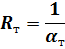
| — термическое сопротивление теплоотдачи со стороны более нагретой среды; |
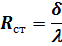
| — термическое сопротивление теплопроводности стенки; |
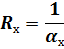
| — термическое сопротивление теплоотдачи со стороны менее нагретой среды. |
Многослойная плоская стенка. Рассмотрим многослойную стенку (рис. 1, б), состоящую из трех слоев толщиной 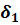 ,
,  ,
, 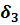 , коэффициенты теплопроводности которых
, коэффициенты теплопроводности которых  ,
, 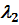 ,
, 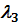 .С одной стороны стенка омывается теплой средой с температурой
.С одной стороны стенка омывается теплой средой с температурой  , с другой — холодной средой с температурой
, с другой — холодной средой с температурой 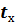 ;
; 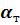 и
и  — коэффициенты теплоотдачи этих сред.
— коэффициенты теплоотдачи этих сред.
Эта задача решается аналогично предыдущей. Поскольку общее термическое сопротивление равно сумме частных, то при расчете многослойной стенки учитывают термическое сопротивление всех ее слоев. В соответствии с формулой (6) полное термическое сопротивление теплопередачи стенки, состоящей из  слоев,
слоев,
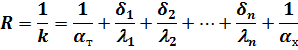
|
или
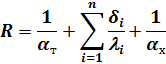
|
Тогда коэффициент теплопередачи многослойной стенки

| (7) |
а плотность теплового потока
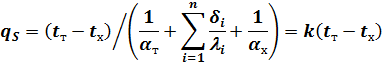
| (8) |
Выражение (4) является частным случаем (8) при 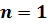 .
.
Тепловой поток через стенку с поверхностью  определится по формуле, которая называется основным уравнением теплопередачи
определится по формуле, которая называется основным уравнением теплопередачи
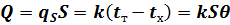
| (9) |
Неизвестные температуры поверхности однослойной стенки находят из выражений (2):
|
|
|
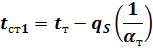
| ; | 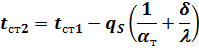
| или | 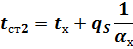
|
Уравнение для определения температуры поверхности на стыке двух любых -гo и 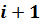 -гo слоев многослойной стенки имеет вид
-гo слоев многослойной стенки имеет вид
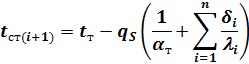
| (10) |
Из уравнения (9) следует, что при заданном температурном перепаде и неизменной площади поверхности теплообмена величиной, определяющей теплопередачу, является коэффициент теплопередачи  .
.
Интенсификация теплопередачи в теплообменных аппаратах является одним из основных путей снижения их габаритных размеров и металлоемкости. Пути интенсификации процесса передачи теплоты могут быть найдены из анализа частных составляющих коэффициента  . Так, для чистой металлической стенки, толщина которой мала по сравнению с коэффициентом теплопроводности (
. Так, для чистой металлической стенки, толщина которой мала по сравнению с коэффициентом теплопроводности (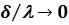 ), уравнение (5) принимает вид
), уравнение (5) принимает вид

|
откуда следует, что значение коэффициента теплопередачи не может быть больше самого малого значения 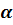 .
.
Проанализируем числовой пример зависимости коэффициента  от заданных
от заданных 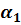 и
и 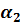 :
:
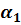 ,Вт/(м2×К) ,Вт/(м2×К)
| |||
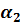 ,Вт/(м2×К) ,Вт/(м2×К)
| |||
 ,Вт/(м2×К) ,Вт/(м2×К)
| 9,95 | 9,99 | 48,78 |
Из этих данных можно сделать следующие выводы:
1) при 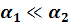 увеличение большего из коэффициентов теплоотдачи (
увеличение большего из коэффициентов теплоотдачи (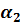 ) почти не дает увеличения
) почти не дает увеличения  ;
;
2) коэффициент теплопередачи увеличивается примерно во столько же раз, во сколько увеличивается меньший (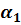 ) из коэффициентов теплоотдачи.
) из коэффициентов теплоотдачи.
Таким образом, при 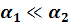 можно считать, что
можно считать, что 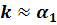 , а при
, а при  , что
, что  .
.
Теплопередающая поверхность аппаратов холодильных машин в процессе эксплуатации загрязняется как со стороны хладагента, так и со стороны хладоносителя. Коэффициенты теплопередачи после длительной эксплуатации могут снизиться на 40-50 % по сравнению с чистыми аппаратами, что объясняется большим термическим сопротивлением загрязнений (табл. 1).
| Таблица 1 | |
| Коэффициенты теплопроводности загрязняющих веществ | |
| Вещество |  ,Вт/(м×К) ,Вт/(м×К)
|
| Смазочное масло | 0,14 |
| Масляная краска | 0,23 |
Водяной камень при  ,кг/м3: ,кг/м3:
| |
| 0,15 | |
| 0,70 | |
| 1,75 | |
| 2,30 | |
Снег при  ,кг/м3: ,кг/м3:
| |
| 0,15 | |
| 0,35 | |
| 0,65 | |
Лед при  кг/м3: кг/м3:
| 2,20 |
|
|
|
| 1.2 | ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ЦИЛИНДРИЧЕСКУЮ СТЕНКУ |
Рассмотрим однослойную цилиндрическую стенку (трубу) с внутренним диаметром 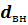 , наружным
, наружным  и длиной
и длиной 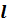 . Стенка трубы характеризуется коэффициентом теплопроводности
. Стенка трубы характеризуется коэффициентом теплопроводности  . Внутри трубы течет более нагретая среда с температурой
. Внутри трубы течет более нагретая среда с температурой  , снаружи — более холодная с температурой
, снаружи — более холодная с температурой 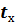 . Суммарные коэффициенты теплоотдачи на внутренней и наружной поверхностях трубы
. Суммарные коэффициенты теплоотдачи на внутренней и наружной поверхностях трубы  и
и 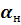 , Температуры поверхностей стенки
, Температуры поверхностей стенки 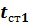 и
и 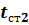 неизвестны (рис. 2).
неизвестны (рис. 2).
Если длина трубы 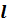 во много раз превосходит ее толщину
во много раз превосходит ее толщину 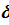 , то потерями теплоты с торцов трубы можно пренебречь. В установившемся тепловом режиме плотность теплового потока, переданного от горячей среды к стенке, прошедшего через нее и переданного от стенки к холодной среде, одинакова.
, то потерями теплоты с торцов трубы можно пренебречь. В установившемся тепловом режиме плотность теплового потока, переданного от горячей среды к стенке, прошедшего через нее и переданного от стенки к холодной среде, одинакова.
Следовательно, можно записать:

| (11) | |
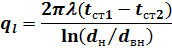
| ||
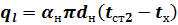
|
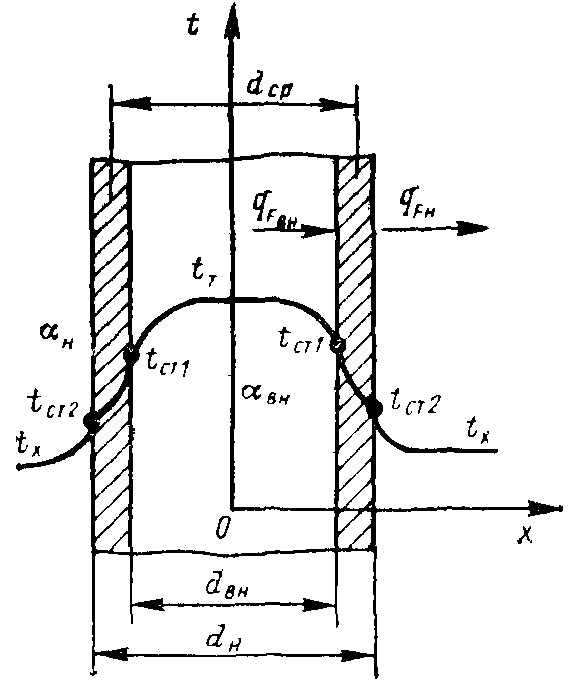
| Рис. 2. Теплопередача через цилиндрическую стенку |
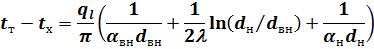
| (12) |
Отсюда находим значение линейной плотности теплового потока
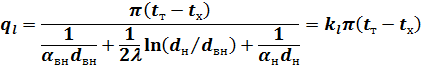
| (13) |
где 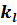 — линейный коэффициент теплопередачи, Вт/(м К), показывающий, какое количество теплоты передается от одной среды к другой через цилиндрическую стенку длиной 1 м в единицу времени при разности температур сред в один градус.
— линейный коэффициент теплопередачи, Вт/(м К), показывающий, какое количество теплоты передается от одной среды к другой через цилиндрическую стенку длиной 1 м в единицу времени при разности температур сред в один градус.
Из выражения (13) следует
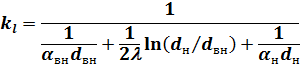
| (14) |
Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи:
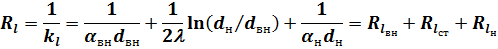
| (15) |
Термические сопротивления теплоотдачи 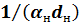 и
и 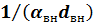 для цилиндрической стенки зависят не только от коэффициента
для цилиндрической стенки зависят не только от коэффициента 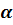 , но и от диаметров соответствующих поверхностей.
, но и от диаметров соответствующих поверхностей.
Тепловой поток через цилиндрическую стенку может быть отнесен к внутренней или наружной ее поверхности. Поверхностная плотность теплового потока с учетом выражения (13) составляет, Вт/м2:
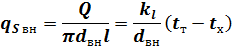
|
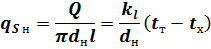
|
Отсюда можно найти коэффициенты теплопередачи, отнесенные к внутренней и наружной поверхностям трубы:
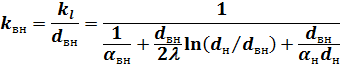
|

|
Соотношения между плотностями тепловых потоков и коэффициентами теплопередачи имеют вид:
|
|
|

| ; | 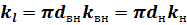
|
В случае передачи теплоты через многослойную цилиндрическую стенку в уравнениях (13)—(15) должны быть учтены термические сопротивления теплопроводности всех ее слоев. Тогда линейный тепловой поток, Вт/м

| (16) |
или

|
а полное термическое сопротивление, (м. К)/Вт
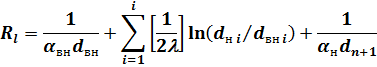
| (17) |
Неизвестные температуры поверхности однослойной цилиндрической стенки находят из соотношений (11):
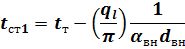
|
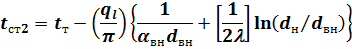
|
Температура поверхности на стыке между 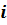 -м и
-м и 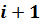 -м слоем многослойной стенки
-м слоем многослойной стенки
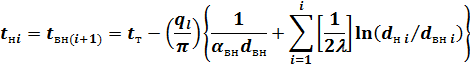
| (18) |
Для практических расчетов формулы могут быть упрощены, если пренебречь разностью площадей наружной и внутренней поверхностей трубы. Это возможно, когда  . Цилиндрическую поверхность трубы можно представить в виде плоской развертки шириной
. Цилиндрическую поверхность трубы можно представить в виде плоской развертки шириной  и для расчета теплопередачи воспользоваться уравнениями (14) и (5) для однородной плоской стенки.
и для расчета теплопередачи воспользоваться уравнениями (14) и (5) для однородной плоской стенки.
Тогда уравнение (13) применительно к трубе длиной 1 м примет вид

|
где  — расчетный диаметр цилиндрической стенки;
— расчетный диаметр цилиндрической стенки; 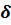 — толщина стенки.
— толщина стенки.
В холодильных теплообменных аппаратах используют трубы с большим коэффициентом теплопроводности и малой по сравнению с диаметром толщиной стенки. С достаточной точностью тепловой поток через цилиндрическую стенку может быть определен по формуле
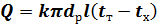
| (19) |
При этом оказывается, что при 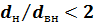 погрешность не более 4 %, а при
погрешность не более 4 %, а при 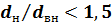 — не более 1,5 %, что вполне приемлемо для технических расчетов. Эту погрешность можно уменьшить, если за расчетный диаметр трубы принять тот, со стороны которого
— не более 1,5 %, что вполне приемлемо для технических расчетов. Эту погрешность можно уменьшить, если за расчетный диаметр трубы принять тот, со стороны которого 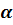 меньше. Если
меньше. Если 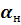 и
и  — величины одного порядка, то
— величины одного порядка, то  —среднеарифметический диаметр между
—среднеарифметический диаметр между  и
и 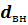 .
.
В целях упрощения расчетов по приведенным формулам термическими сопротивлениями пренебрегают как относительно малыми величинами.
| 1.3 | ТЕПЛОВАЯ ИЗОЛЯЦИЯ. КРИТИЧЕСКИЙ ДИАМЕТР ИЗОЛЯЦИИ |
В качестве изоляционных применяют материалы как органического, так и неорганического происхождения с коэффициентом теплопроводности 0,35–0,015 Вт/(м×К).
Рациональная толщина слоя теплоизоляции зависит от эффективности применяемого изоляционного материала и его стоимости.
|
|
|
Рассмотрим факторы, влияющие на передачу теплоты через слой изоляции, на примере стального изолированного трубопровода. Линейное термическое сопротивление в соответствии с формулой (17)

| (20) |
где четыре слагаемых правой части уравнения представляют собой соответственно термические сопротивления теплоотдачи внутри трубы, теплопроводности стенки, теплопроводности изоляции, теплоотдачи на наружной поверхности теплоизоляции.
Первое и второе слагаемые правой части уравнения не зависят от изменения наружного диаметра изоляции 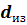 , на графике (рис. 3, а) сумма этих сопротивлений (
, на графике (рис. 3, а) сумма этих сопротивлений ( ) изображается прямой, параллельной оси абсцисс. Третье слагаемое
) изображается прямой, параллельной оси абсцисс. Третье слагаемое  — сопротивление теплопроводности изоляции с ростом ее толщины возрастает, а последнее
— сопротивление теплопроводности изоляции с ростом ее толщины возрастает, а последнее  — сопротивление теплоотдачи на наружной поверхности с ростом
— сопротивление теплоотдачи на наружной поверхности с ростом 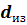 уменьшается.
уменьшается.
Таким образом, при наложении слоя тепловой изоляции на трубу происходит не только уменьшение тепловых потерь, Связанных с дополнительным сопротивлением слоя изоляции, но одновременно улучшается отвод теплоты от внешней поверхности в окружающую среду за счет увеличения площади наружной поверхности. Следовательно, суммарный тепловой поток через изолированную трубу может как увеличиваться, так и уменьшаться.
| Рис. 3. К определению критического диаметра теплоизоляции |
 в точке 2 имеет явно выраженный минимум. Если учесть, что термическое сопротивление обратно пропорционально коэффициенту теплопередачи, то минимальному термическому сопротивлению
в точке 2 имеет явно выраженный минимум. Если учесть, что термическое сопротивление обратно пропорционально коэффициенту теплопередачи, то минимальному термическому сопротивлению  , в точке 2 будет соответствовать максимальная плотность теплового потока
, в точке 2 будет соответствовать максимальная плотность теплового потока 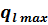 , точка 20.
, точка 20.
Значение внешнего диаметра теплоизоляции, при котором тепловой поток достигает максимального значения, называется критическим диаметром изоляции.
Из рис. 3, а следует: 1) при  увеличение толщины изоляции приводит к возрастанию теплового потока по сравнению с неизолированным трубопроводом (точка 1), т. е. к росту тепловых потерь, которые при
увеличение толщины изоляции приводит к возрастанию теплового потока по сравнению с неизолированным трубопроводом (точка 1), т. е. к росту тепловых потерь, которые при  достигают максимума; 2) при
достигают максимума; 2) при 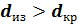 увеличение толщины изоляции приводит к уменьшению теплового потока, 3) при
увеличение толщины изоляции приводит к уменьшению теплового потока, 3) при 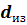 (точка 3) тепловой поток становится равным тепловому потоку неизолированного трубопровода:
(точка 3) тепловой поток становится равным тепловому потоку неизолированного трубопровода:  . Это значит, что слой изоляции
. Это значит, что слой изоляции 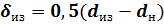 установлен напрасно, т. е. изоляционный материал выбран неверно.
установлен напрасно, т. е. изоляционный материал выбран неверно.
Наружный диаметр изоляции  в экстремальной точке 2 может быть определен из уравнения (20), если взять первую производную от
в экстремальной точке 2 может быть определен из уравнения (20), если взять первую производную от 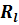 по
по 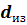 и приравнять ее к нулю:
и приравнять ее к нулю:
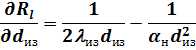
|
откуда
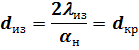
| (21) |
Из выражения (19.21) следует, что критический диаметр теплоизоляции 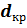 зависит только от теплопроводности изоляционного материала
зависит только от теплопроводности изоляционного материала 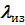 и коэффициента теплоотдачи
и коэффициента теплоотдачи 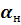 от наружной поверхности изоляции к окружающей среде и совершенно не зависит от размеров трубопровода. Поэтому для одной и той же трубы диаметра
от наружной поверхности изоляции к окружающей среде и совершенно не зависит от размеров трубопровода. Поэтому для одной и той же трубы диаметра  в зависимости от применяемого изоляционного материала (кривые I, II, III на рис. 3, б) критический диаметр изоляции может иметь различные значения:
в зависимости от применяемого изоляционного материала (кривые I, II, III на рис. 3, б) критический диаметр изоляции может иметь различные значения: 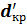 ,
, 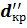 ,
, 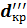 .
.
Из графика видно: 1) при одной и той же толщине слоя теплоизоляции  наибольшее уменьшение теплового потока достигается при изоляционном материале, для которого
наибольшее уменьшение теплового потока достигается при изоляционном материале, для которого 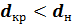 ; действительно,
; действительно, 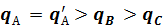 ; 2) толщину изоляции трубопровода следует увеличивать только до тех пор, пока происходит резкое снижение теплового потока, так как дальнейшее увеличение слоя изоляции малоэффективно. Следовательно, для правильного выбора типа изоляционного материала необходимо, чтобы
; 2) толщину изоляции трубопровода следует увеличивать только до тех пор, пока происходит резкое снижение теплового потока, так как дальнейшее увеличение слоя изоляции малоэффективно. Следовательно, для правильного выбора типа изоляционного материала необходимо, чтобы 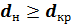 или
или  . Тогда
. Тогда

| (22) |
Из неравенства (22) следует, что чем меньше диаметр изолируемого трубопровода, тем более эффективной должна быть теплоизоляция, т. е. тем меньше должен быть ее коэффициент теплопроводности.
В случае установки теплоизоляции на плоской стенке не возникает вопроса о принципиальной пригодности того или другого материала. Любой изоляционный материал будет уменьшать тепловой поток, так как размеры площади поверхности теплопередачи в направлении теплового потока не изменяются ( ).
).
Толщина слоя теплоизоляции ограждающих конструкций холодильных объектов определяется из уравнения (7):
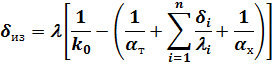
| (23) |
где  — нормативный коэффициент теплопередачи (СНиП 105–74).
— нормативный коэффициент теплопередачи (СНиП 105–74).
| 1.4 | ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ОРЕБРЕННЫЕ ПОВЕРХНОСТИ |
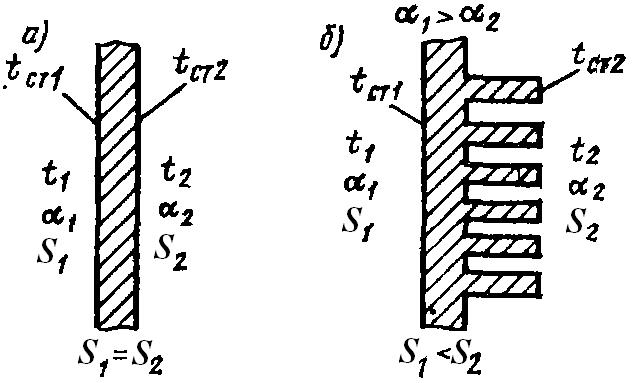
| Рис. 4. Оребрение поверхности: а – плоская стенка; б – оребренная стенка |
 , то оребряют поверхность, контактирующую со второй средой (рис. 4). Отношение большей площади поверхности стенки к меньшей называется коэффициентом оребрения
, то оребряют поверхность, контактирующую со второй средой (рис. 4). Отношение большей площади поверхности стенки к меньшей называется коэффициентом оребрения  :
:
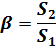
| (24) |
Для рассмотрения сущности такого метода интенсификации получим приближенную формулу для расчета теплового потока, проходящего через стенку, которая с каждой из сторон имеет различную площадь поверхности, в предположении, что термическим сопротивлением стенки можно пренебречь: 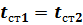 . Тепловые потоки, передаваемые и воспринимаемые каждой из сред при установившемся тепловом режиме, равны между собой, т. е.
. Тепловые потоки, передаваемые и воспринимаемые каждой из сред при установившемся тепловом режиме, равны между собой, т. е.
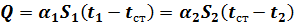
|
Решив эти уравнения относительно частных температурных напоров и сложив почленно, получим

| (25) |
где
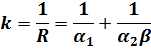
| — коэффициент теплопередачи, отнесенный к меньшей поверхности  теплообмена; теплообмена;
| ||
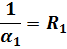
| ; | 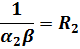
| — частные термические сопротивления теплоотдачи. |
Для плоской поверхности  , и если
, и если  , то общее термическое сопротивление будет определяться термическим сопротивлением второй среды:
, то общее термическое сопротивление будет определяться термическим сопротивлением второй среды: 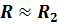 .
.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 2134; Нарушение авторских прав?; Мы поможем в написании вашей работы!