
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тепловой изоляцией называют любое покрытие, способствующее уменьшению теплового потока через данную поверхность. 4 страница
|
|
|
|
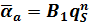
| (63) |
где 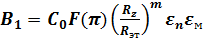 — постоянная, учитывающая влияние на теплообмен всех факторов, кроме плотности теплового потока
— постоянная, учитывающая влияние на теплообмен всех факторов, кроме плотности теплового потока 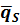 .
.
Для конденсатора расчетная формула коэффициентов теплоотдачи при конденсации на многорядном пучке труб имеет вид

| (64) |
При постоянной температуре конденсации и неизменной конструкции аппарата уравнение (19.64) можно представить в виде

| (65) |
где

| — постоянная, учитывающая влияние на теплообмен всех факторов, кроме температурного напора  . .
|
Для графоаналитического расчета зависимости (63) и (65) представляют в виде функции  . Из уравнения (63)
. Из уравнения (63)  можно получить
можно получить

| (66) |
где  (рис. 10, а).
(рис. 10, а).
Аналогично из уравнения (65)  получаем
получаем

| (67) |
где  (рис. 10, б).
(рис. 10, б).
Плотность теплового потока от внутренней стенки трубы к воде (конденсатор) или от хладоносителя к стенке трубы (испаритель) с учетом всех термических сопротивлений, кроме сопротивления со стороны хладагента, определяется по формуле

| (68) |
Здесь плотность теплового потока должна быть отнесена к наружной поверхности, т.е.  как было принято при определении
как было принято при определении 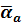 .
.
Температурный напор  для расчета испарителя и
для расчета испарителя и  – конденсатора.
– конденсатора.
Для неоребренных труб  ;
;  .
.
При графоаналитическом методе (рис. 10, в, с) по оси абсцисс в масштабе откладывают значение  . Из противоположных концов полученного отрезка, задаваясь рядом значений
. Из противоположных концов полученного отрезка, задаваясь рядом значений  и
и  , строят зависимости
, строят зависимости  и
и  , используя уравнения (66)–(68), причем выражение (68) является уравнением прямой линии, т. е. для ее построения достаточно двух точек, одна из которых соответствует
, используя уравнения (66)–(68), причем выражение (68) является уравнением прямой линии, т. е. для ее построения достаточно двух точек, одна из которых соответствует  , а вторая любой величине. При этом
, а вторая любой величине. При этом  , а величины
, а величины  и
и  изменяются от
изменяются от  до
до  . Пересечение кривых на графике – точка Р (рис. 10, в для испарителя и рис. 10, с для конденсатора) соответствует стационарному режиму работы аппарата, при котором
. Пересечение кривых на графике – точка Р (рис. 10, в для испарителя и рис. 10, с для конденсатора) соответствует стационарному режиму работы аппарата, при котором  .
.
|
|
|
6. По известному значению средней плотности теплового потока 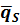 , oтнесенного к наружной поверхности, и тепловому потоку
, oтнесенного к наружной поверхности, и тепловому потоку 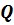 определяют требуемую площадь наружной поверхности теплообмена — по формуле (52). Величины
определяют требуемую площадь наружной поверхности теплообмена — по формуле (52). Величины  и
и 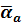 находят из соотношения (61).
находят из соотношения (61).
В дальнейшем при конструктивном расчете делают компоновку аппарата и определяют его длину, число ходов, число труб, диаметр обечайки и т. п. При проектном расчете выбирают ближайший по площади поверхности аппарат, для которого выполняют проверочный расчет.
| 1.5.3 | Проверочный расчет теплообменного аппарата |
В настоящее время достаточно строгие методы проверочного расчета существуют только для рекуперативных теплообменников, у которых коэффициенты теплоотдачи в процессе переноса теплоты остаются неизменными и не зависят от температурных напоров. Целью проверочного расчета аппарата заданной конструкции является определение его производительности и температур потоков на выходе  ,
,  (рис. 9) при заданных площади поверхности теплообмена
(рис. 9) при заданных площади поверхности теплообмена  , расходах сред
, расходах сред 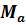 ,
,  и их температурах на входе
и их температурах на входе  ,
,  .
.
На первом этапе исходя из конструкции аппарата определяют действительные скорости движения каждой из сред и по ранее описанной методике рассчитывают коэффициент теплопередачи. Теплофизические характеристики каждой из сред ( ,
,  ,
,  и т.д.) принимают равными принятым при определении требуемой поверхности теплообмена. В случае если проводится проверочный расчет эксплуатируемого аппарата при переводе его на другой режим работы, в качестве первого приближения можно принять значения теплофизических характеристик по температурам
и т.д.) принимают равными принятым при определении требуемой поверхности теплообмена. В случае если проводится проверочный расчет эксплуатируемого аппарата при переводе его на другой режим работы, в качестве первого приближения можно принять значения теплофизических характеристик по температурам  и
и  , или (с учетом ожидаемых изменений в процессе) по приближенным средним температурам
, или (с учетом ожидаемых изменений в процессе) по приближенным средним температурам  и
и  с последующим их уточнением по результатам расчета.
с последующим их уточнением по результатам расчета.
Примем, что аппарат противоточный и тепловой эквивалент потока
|
|
|
 , что соответствует теплообменнику по рис. 9, б, в. Конечная температура потока
, что соответствует теплообменнику по рис. 9, б, в. Конечная температура потока 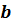 определится по уравнению
определится по уравнению

| (69) |
а потока  — по уравнению
— по уравнению

| (70) |
Тепловой поток в аппарате

| (71) |
Здесь величина Ф для противотока определяется уравнением

| (72) |
Таким образом, рассчитав коэффициент теплопередачи для данного аппарата с площадью поверхности  , к которой этот коэффициент отнесен, можно определить по формулам (69)–(71) величины
, к которой этот коэффициент отнесен, можно определить по формулам (69)–(71) величины  ,
,  и
и 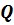
В конденсаторе и испарителе температуры жидкого хладагента не изменяются:  (рис. 9, б, в), тогда тепловой эквивалент потока хладагента бесконечно велик:
(рис. 9, б, в), тогда тепловой эквивалент потока хладагента бесконечно велик:  . В этом случае прямоток и противоток равнозначны и при условии, что
. В этом случае прямоток и противоток равнозначны и при условии, что  , уравнение (72) примет вид
, уравнение (72) примет вид
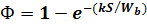
| (73) |
Однако такой метод для проверочного расчета испарителей и конденсаторов является приближенным, так как их тепловая нагрузка зависит от температур конденсации и кипения, а коэффициент теплопередачи  .
.
Можно предложить следующую схему приближенного проверочного расчета этих аппаратов. При заданных расходах 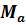 ,
,  , температурах сред
, температурах сред  ,
,  и тепловом потоке
и тепловом потоке 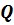 по уравнению (71) находят значение вспомогательной функции
по уравнению (71) находят значение вспомогательной функции  , обеспечивающее данный режим работы аппарата. Этому режиму соответствует предельное минимальное значение коэффициента теплопередачи, определяемое по уравнению (73), которое после преобразований можно представить в виде
, обеспечивающее данный режим работы аппарата. Этому режиму соответствует предельное минимальное значение коэффициента теплопередачи, определяемое по уравнению (73), которое после преобразований можно представить в виде
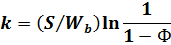
| (74) |
При заданных 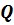 и конструкции аппарата известна также и величина
и конструкции аппарата известна также и величина  по уравнению (63) находят коэффициент теплоотдачи при кипении, а по уравнению (65) при конденсации. Для этого последнее уравнение преобразуют в функцию
по уравнению (63) находят коэффициент теплоотдачи при кипении, а по уравнению (65) при конденсации. Для этого последнее уравнение преобразуют в функцию 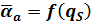 :
:

| (74) |
откуда  , или
, или

| (75) |
Для заданной конструкции уточняют значение скорости потока b и определяют коэффициент теплопередачи аппарата с учетом всех возможных термических сопротивлений  . Если полученное значение
. Если полученное значение  равно рассчитанному по уравнению (74) значению k, то аппарат будет работать в заданном режиме. Если
равно рассчитанному по уравнению (74) значению k, то аппарат будет работать в заданном режиме. Если  , то аппарат сможет обеспечить нормальную работу холодильной машины в более благоприятных условиях (при повышенной температуре кипения или пониженной температуре конденсации), что также приемлемо. При
, то аппарат сможет обеспечить нормальную работу холодильной машины в более благоприятных условиях (при повышенной температуре кипения или пониженной температуре конденсации), что также приемлемо. При  заданные условия не могут быть обеспечены и требуется или увеличить площадь поверхности, или допустить работу машины при параметрах, менее благоприятных, чем расчетные.
заданные условия не могут быть обеспечены и требуется или увеличить площадь поверхности, или допустить работу машины при параметрах, менее благоприятных, чем расчетные.
|
|
|
Если температуры сред вдоль поверхности теплообмена изменяются незначительно (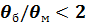 ), то можно принять
), то можно принять  . Из уравнения теплового баланса (49) определяют конечные температуры потоков:
. Из уравнения теплового баланса (49) определяют конечные температуры потоков:

| ; | 
| (76) |
где тепловой поток 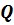 может быть найден по уравнению (51):
может быть найден по уравнению (51):
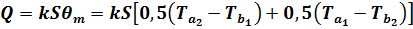
| (77) |
После подстановки в него значений  и
и  , по (76) имеем
, по (76) имеем

| (78) |
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 713; Нарушение авторских прав?; Мы поможем в написании вашей работы!