Работа при различных изопроцессах

Адиабатический процесс. Уравнение Пуассона.

Адиабатическим называется процесс, при ктором отсутствует теплообмен вещества с окружающей средой, например распространение звука в среде. Из 1 начала термодинамики 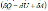для адиабатического процесса следует, что: 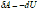(8.19), т е внешняя работа осуществляется за счет изменения внутренней энергии. Используя выражения: 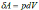и ,

Где P – давление, - молярная теплоёмкость газа при постоянном объёме, для произвольной массы газа урав-нение (8.19) выражается в виде: (8.20)

Обозначив , после преобразований можно перейти к выражению: 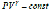(8.21). Полученное уравнение представляет выражение адиабатического процесса или уравнение Пуассана. Используя уравнение Клапейрона 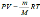, получаем:

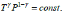(8.22); представляет уравнения адиабатического процесса, а - показатель адиабаты.

Диаграмма адиабатического процесса (адиабата) в координатах P,V изображается гиперболой (рис.8.5). на рис.8.5 видно, что адиабата более крута 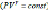, чем изотерма (PV=const). Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обуслевлено не только уменьшением его объёма, как при изотермическом сжатии, но и повышением температуры.

Рис.8.5

Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из параметров сохраняется постоянным.

Изохорный процесс (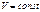). 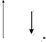Рис. 7.2

Диаграмма этого процесса изображается прямой, параллельной оси ординат (рис. 7. 2). При этом процессе газ не совершает работы, т.е.: (7.19). Тогда, согласно I началу термодинамики, вся теплота, сообщаемая газу, идёт на увеличение его внутренней энергии: (7.20). Так как: ,(7.21) C_v – удельная теплоемкость газа при постоянном объеме, то для произвольной массы газа получим: 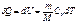(7.22);

Изобарный процесс (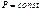). Диаграмма этого процесса в координатах изображается прямой, параллельной оси 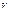. Работа газа при увеличении объема от значения до 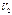равна: (7.23)

и определяется площадью серого прямоугольника (рис 7.3). Рис. 7.3.

Если использовать уравнение Клапейрона – Менделеева, 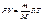для двух состояний 1 и 2, то: ; (7.24)

Из последнего выражения определяется физический смысл молярной газовой постоянной : если 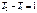^оК, то для 1 моля газа 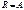, т.е. численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1^оК.

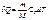В изобарном процессе при сообщении телу массой количества теплоты: ,(7.25); C_p – удельная теплоемкость газа при постоянном давлении, то еговнутренняя энергия возрастёт на величину: 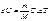(7.26)

Изотермический процесс.

Изотермический процесс описывается законом Бойля-Мариотта. Диаграмма этого процесса в координатах представляет собой гиперболу.

Работа изотермического расширения газа определяется:

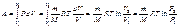(7.27). Так как при внутренняя энергия идеального газа не изменяется , то для изотермического процесса выполняется условие , т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: 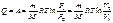(7.28)

Дата добавления: 2017-01-14