Порядок выполнения работы. Все студенты группы делятся на подгруппы и выполняют следующие задания:

Варианты задания

Все студенты группы делятся на подгруппы и выполняют следующие задания:

1. Найти площадь фигуры, ограниченной линиями:

y=sin(x)+2

y=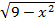

y=0

2. Найти площадь фигуры, ограниченной линиями:

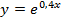
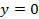
3. Найти площадь фигуры, ограниченной линиями:

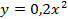
x=0

y=4

4. Найти площадь фигуры, ограниченной линиями:

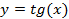
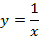
y=0

x=3

Для получения выборки случайных чисел с заданным распределением можно воспользоваться функцией «Генерация случайных чисел» из меню «Анализ данных».

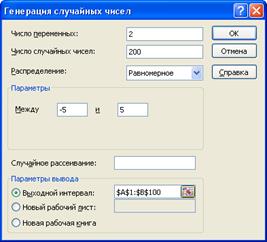
Рисунок 2.2 – Генерация случайных чисел

Таблица 2.1 Создание таблицы данных

	A	B	C
	-2,6943	-1,5031	=ЕСЛИ(A1*A1+B1*B1<=25;1;0)
	0,62639	-4,3026	=ЕСЛИ(A2*A2+B2*B2<=25;1;0)
	-4,6047	-1,3075	=ЕСЛИ(A3*A3+B3*B3<=25;1;0)
	-4,7421	0,30716	=ЕСЛИ(A4*A4+B4*B4<=25;1;0)
	3,5735	-4,4195	=ЕСЛИ(A5*A5+B5*B5<=25;1;0)
	-4,6508	2,6851	=ЕСЛИ(A148*A148+B148*B148<=25;1;0)
	-3,8592	-4,1964	=ЕСЛИ(A149*A149+B149*B149<=25;1;0)
	2,4614	3,3382	=ЕСЛИ(A150*A150+B150*B150<=25;1;0)
		число попаданий	=СУММ(C1:C150)
		число наблюдений	=СЧЁТ(C1:C150)
		площадь круга	=(C151/C152)*100

Для изучения влияния статистической ошибки при моделирова­нии задача решалась для различных значений п, равных 150, 200, 500, 1000, 2000, 5000 и 10 000. Кроме того, при каждом п было про­ведено 10 прогонов, в каждом из которых использовались различные последовательности случайных чисел из интервала [-5, 5].

Таблица 2.2 – Результаты обработки

№	Оценки площади круга при данном числе испытаний n
		80,5		78,6	79,55	78,32
		79,5	79,6	78,8	78,85	79,26
		81,5	76,6	77,6	79,1	77,22
			78,8		79,55	79,34
			76,2	79,8	79,4	79,22
		77,5	76,6	77,6	77,4	77,44
		81,5	80,4	78,5	78,1	79,28
		76,5	81,8	79,7	77,2	78,82
		80,5	76,6	76,4	77,76	78,74
			81,2		78,4	77,74
Среднее	78,1	78,35	78,38	78,5	78,531	78,538
Дисперсия	23,65556	14,28056	5,035111	1,306667	0,789499	0,658618
	Расчетное значение	78,54

В таблице приведены результаты эксперимента, исходя из которых можно сделать следующие заключения.

1. С ростом числа генерируемых точек (т. е. продолжительности прогона модели) оценки площади круга приближаются к точному значению (78,54 см²). На рис. 3.3 показаны оценки площади прогонов 1 и 2 в зависимости от продолжительности прогона п. Мы видим, что сначала оценки колеблются около точного значения, а затем стабилизируются. Это условие обычно достигается после по­вторения эксперимента достаточное количество раз. Наблюдаемое явление типично для результатов любой имитационной модели. Обычно в большинстве имитационных моделей нас интересуют результаты, полученные в стационарных условиях.

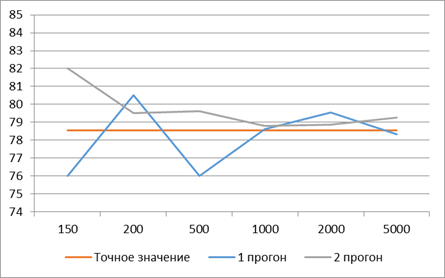
Рисунок 2.3 – Обработка результатов

2. Влияние переходных условий умень­шается, если усреднить результаты 10 серий. Это иллюстрирует рис. 3.4, на котором показана зависимость среднего от п. Кроме того, на рисунках видно, что для каждого п при достижении стацио­нарных условий дисперсия убывает. При возрастании п от 150 до 200 дисперсия резко уменьшается с 23,66 до 14,25. За исключением этого интервала, столь резкого уменьшения дисперсии нигде больше не наблюдается. Последнее замечание указывает на то, что сущест­вует предел, за которым увеличение продолжительности прогона модели уже не дает существенного повышения точности результа­та, измеряемой дисперсией. Это замечание представляется чрезвы­чайно важным, поскольку затраты на эксплуатацию имитационной модели прямо пропорциональны продолжительности прогонов. Поэтому желательно найти компромисс между большой точностью (т. е. малой дисперсией) и небольшими затратами на процедуру получения результатов.

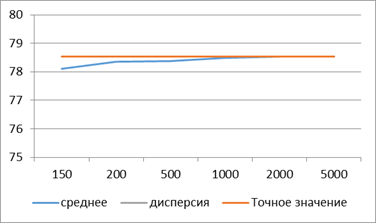
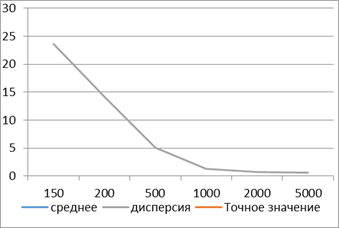
Рисунок 2.4 – Результаты исследований

3. Ввиду того что оценки площади имеют разброс, важно, чтобы результаты эксперимента, связанного с моделированием, были вы­ражены в виде доверительных интервалов, показывающих величину отклонения от точного значения. В рассматриваемом примере, если А представляет собой точное значение площади, а и s² — среднее и дисперсию N наблюдений, то 100 (1—α)%-ный доверительный ин­тервал для А задается как

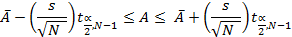
Дата добавления: 2017-01-14