Практическое занятие №2 1 страница

Ход работы

Практическое занятие №1

«Линейное программирование. Графический метод решения задач. Анализ чувствительности»

Цель: научиться решать задачи линейного программирования графически и

алгебраически, а так же проводить анализ чувствительности.

Задача: решить задачу согласно своему варианту.

Формулировка задачи линейного программирования состоит из шагов.

Шаг 1. Определение переменных задачи, значения которых нужно получить в пределах существующих ограничений.

Шаг 2. Определение цели и ограничений на ресурсы.

Шаг 3. Описание цели через переменные задачи.

Шаг 4. Описание ограничений через переменные задачи.

Пример 1. Завод-производитель выпускает два различных типа деталей: Х и Y. Завод располагает фондом рабочего времени в 4000 человеко-часов в неделю. Для производства одной детали типа X требуется 1 человек а, для производства одной детали типа Y — 2 человеко-часов Производственные мощности завода позволяют выпускать максимум 2250 деталей типа Х и 1750 деталей типа Y в неделю. Каждая деталь типа Х требует 2 кг металлических стержней и 5 кг листового металла, а для производства одной детали типа Y необходимо 5 кг металлических стержней и 2 кг листового металла. Уровень запасов каждого вида металла составляет 10000 кг в неделю. Кроме того, еженедельно завод поставляет 600 деталей типа Х своему постоянному заказчику. Существует также профсоюзное соглашение, в соответствии с которым общее число производимых в течение одной недели деталей должно составлять не менее 1500 штук. Сколько деталей каждого типа следует производить, чтобы максимизировать общий доход за неделю, если доход от производства одной детали типа Х составляет 30 рублей, а от производства одной детали типа Y — 40 рублей?

Решение

Шаг 1. Необходимо произвести х деталей типа Х и у деталей типа Y в неделю.

Шаг 2. Цель состоит в максимизации общего дохода за неделю. Ограничения:

- фонд рабочего времени (4000 человеко-часов в неделю);

- производственная мощность (оборудование позволяет выпускать не более 2250 деталей типа Х и 1750 типа Y в неделю);

- металлические стержни (максимально 10000 кг в неделю);

- листовой металл (максимально 10000 кг в неделю).

Кроме того, существуют ограничения на минимальный объем производства деталей каждого вида:

- постоянные заказы (число произведенных деталей Х должно быть достаточным для удовлетворения размера постоянных заказов);

- профсоюзное соглашение (общее число деталей (х + у) не должно быть ниже объема, предусмотренного соглашением).

Шаг 3. Целевая функция. Пусть Р — общий доход за неделю, где

Р = 30 х + 40 у (А.1)

Шаг 4. Для каждого ограничения на ресурсы, необходимые для производства х деталей типа Х и у деталей типа Y в неделю, ниже приведены количества и соответствующие им максимальные уровни наличных ресурсов.

Требуемый фонд рабочего времени:

х + 2 у 4000 (А.2)

Требуемая производственная мощность:

х 2250 (А.3)

у 1750 (А.4)

Требуемое количество металлических стержней: 2 х + 5у 10000 (А.5)

Требуемое количество листового металла:

5 х +2 у 10000 (А.6)

Постоянные заказы:

х 600 (А.7)

Профсоюзное соглашение:

х + у 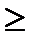1500 (А.8)

Условие неотрицательности:

х, у 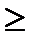0 (А.9)

Решение задачи линейного программирования

Чтобы продемонстрировать этот алгоритм, обратимся к примеру 1, в котором рассматривается производство деталей типов Х и Y к автомобилям. Введем дополнительную переменную: в первое ограничение вводится переменная s₁ во второе — s₂ и т.д. Кроме того, примем предпосылку о неотрицательности значений этих переменных, т.е. s_i 0. Это значит, что дополнительные переменные прибавляются к левым частям всех ограничений знака " 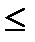" и вычитаются из левых частей ограничений знака " ".

Максимизировать:

Р = 30 х + 40 у (А.1)

при ограничениях:

Фонд рабочего времени:

1 x + 2 y + s₁ = 4000 (А.19)

Производственная мощность:

х + s₂ = 2250 (А.20)

у + s₃ = 1750 (А.21)

Металлические стержни:

2 х + 5 y + s₄ = 10000 (А.22)

Листовой металл:

5 х + 2 у + s₅ = 10000 (А.23)

Постоянные заказы:

х – s₆ = 600 (А.24)

Профсоюзное соглашение:

х + у – s₇ = 1500 (А.25)

Условие неотрицательности:

х, у 0 (А.9)

Предположим, что в течение недели выпускается 1000 деталей каждого типа, тогда используемое число человеко-часов составит 3000. Поскольку максимальный фонд рабочего времени равен 4000 человеко-часов, резерв времени, или остаток, составит 1000 человеко-часов. Следовательно, для данной комбинации х - у и s₁ принимают значение, равное 1000.

Рассмотрим ограничение на постоянные заказы в случае, когда выпускается 1000 деталей типа X. Минимальное число деталей типа Х составляет в соответствии с данным ограничением 600 штук, следовательно, уровень производства, равный 1000 деталей, порождает излишек в 400 штук сверх минимального количества. Таким образом,s₆ принимает значение, равное 400.

Если задача содержит только две переменные, то определить множество допустимых значений можно графически. Однако в случае решения задачи с множеством переменных необходимо прибегнуть к алгебраическому методу решения.

Графическое решение задачи линейного программирования

Пример 1.3. Обратимся к примеру 1.1.

Решение

Допустимые области для каждого из ограничений задачи изображены на рисунке А.1. Допустимое множество, содержащее все возможные ассортиментные наборы продукции для данной задачи, осталось незаштрихованным на рисунке А.1.

Чтобы построить линию уровня функции (А.1) для типичного значения дохода, выберем принадлежащую допустимому множеству точку с координатами х = 1000, у = 1000. Для этого ассортиментного набора общий доход за неделю составит 7000 рублей в неделю.

В качестве контрольной линии уровня будем использовать прямую

70000 = 30 х + 4 у (А.26)

Эта прямая проходит также через точку с координатами х = 0, у = 1750. На рисунке 2.1 она изображена пунктирной линией. Движение параллельно этой прямой в направлении увеличения дохода приводит нас в точку А, которая является последним допустимым решением.

Лимитирующими являются ограничения на:

Фонд рабочего времени:

х + 2 у < 4000 (А.27)

Листовой металл:

5 х + 2 у < 10000 (А.28)

Решив соответствующую систему уравнений, получим х = 1500 и после подстановки значения х в систему получим значение у = 1250.

Рисунок А.1 - Задача линейного программирования для выпуска деталей типа Х и У к автомобилям в неделю

Оптимальным ассортиментным набором является выпуск 1500 деталей типа Х и 1250 деталей типа Y в неделю. Таким образом, максимальный доход за неделю исходя из функции (А.1) составит 95000 руб. в неделю.

Нетрудно установить, что значения остаточных переменных в ограничениях на производственные мощности равны 750 (s₂) для деталей типа Х и 500 (s₃) для деталей типа Y. Остаточная переменная ограничения на металлические стержни 750 (s₄) кг в неделю. Избыточная переменная ограничения на постоянные заказы 900 s₆ деталей в неделю сверх минимального количества, необходимого для удовлетворения постоянных заказов. Избыток по профсоюзному соглашению составил 1250 (s₇) деталей в неделю сверх минимального количества деталей, оговоренного в профсоюзном соглашении.

Анализ чувствительности

Существуют три аспекта решения задач линейного программирования, которые необходимо подвергнуть тщательному изучению:

- воздействие дополнительного количества лимитирующего ресурса;

- воздействие дополнительного количества нелимитирующего ресурса;

- воздействие изменений в коэффициентах целевой функции.

Рассмотрим каждую из этих ситуаций в отдельности. При дальнейшем рассмотрении примем предпосылку о том, что в любой момент времени изменяется только один параметр.

Воздействие изменений в обеспечении лимитирующим ресурсом на решение задачи линейного программирования

Пример 4. Обратимся к примерам 1 и 3. Из примера 3 мы знаем, что лимитирующими являются ограничения на фонд рабочего времени и на листовой металл. Обратимся к графику, изображенному на рисунке А.2. Жесткость ограничения на листовой металл снижается по мере перемещения линии ограничения параллельно ее исходному положению в противоположном направлении от начала координат. Допустимое множество расширяется, а оптимальная крайняя точка перемещается вниз то линии ограничения на фонд рабочего времени, что увеличивает х и уменьшает у. Снижение жесткости ограничения на листовой металл является эффективным до тех пор, пока линия ограничения не достигнет точки пересечения ограничений на фонд рабочего времени и производственные мощности для деталей типа X, т.е. точки В. Если и далее снижать жесткость ограничения на листовой металл, оно перестанет быть лимитирующим, что приведет к появлению остатка в виде неиспользованного листового металла.

Новой оптимальной крайней точкой является теперь точка В. Координаты точки В можно определить, решив систему уравнений для ограничений на фонд рабочего времени и производственные мощности для детали X.

Так как х = 2250 (производственные мощности), то, подставив его в первое уравнение, у = 875 деталей.

Новым оптимальным ассортиментным набором является производство 2250 деталей типа Х и 875 деталей типа Y в неделю. Этот ассортиментный набор дает максимальный доход, равный 102500 рублей в неделю из расчета функции (А.1). Таким образом, увеличение дохода составит 7500 рублей в неделю. Количество листового металла, используемое для производства данного ассортиментного набора, равно 13000 кг в неделю. Оно превышает начальное количество на 3000 кг в неделю. В новой оптимальной точке фонд рабочего времени и производственные мощности для деталей Х также используются максимально.

Дополнительное количество листового металла — 3000 кг — позволяет получать дополнительный доход, равный 7500 руб. в неделю, следовательно, теневая цена данного ресурса составит 7500: 3000 = 2,50 рублей за 1 кг. Каждый дополнительный килограмм листового металла ведет к увеличению еженедельного дохода в 2,50 рублей. Из этого следует, что сверхнормативный запас этого ресурса целесообразен только в случае, если стоимость получения любого дополнительного количества ресурса не превышает 2,50 рублей за 1 кг ресурса.

Предположив, что ограничение на листовой металл остается неизменным, применим аналогичную процедуру ко второму лимитирующему ограничению.

Рисунок А.2 - Задача линейного программирования для производства деталей типа Х и У в неделю

Если жесткость ограничения на фонд рабочего времени снизилась на единицу, т.е. появилась возможность использовать 1 человеко-часов рабочего времени дополнительно, то тогда данное ограничение принимает вид:

x + 2y 4001 (А.29)

Данное ограничение параллельно первоначальному, но его линия находится дальше от начала координат по сравнению с исходной линией. На рисунке А.2 легко видеть, что точка пересечения ограничения на листовой металл и нового ограничения на фонд рабочего времени все еще является оптимальной крайней точкой. В данном случае оптимальным решением является точка с координатами х = 1499,75 и у = 1250,625, что приводит и к значению целевой функции Рmах ⁼ 95017,50 рублей. Таким образом, значение целевой функции увеличилось на 17,50 рублей. Теневая цена фонда рабочего времени составляет 17,50 рублей за 1 человеко-часов. Если можно получить один дополнительный час рабочего времени за дополнительные 17,50 рублей или менее, то это необходимо использовать. Если же стоимость 1 человеко-часов превышает 17,50 рублей, то дополнительное количество рабочего времени использовать нецелесообразно.

Какое количество дополнительного рабочего времени следует купить? Поскольку линия ограничения на фонд рабочего времени движется параллельно своему исходному положению в направлении от начала координат, она стремится к точке пересечения ограничений на листовой металл и металлические стержни к точке С. Если и далее снижать жесткость ограничения на фонд рабочего времени, то оно перестанет быть лимитирующим, и дальнейшее привлечение дополнительного рабочего времени нецелесообразно. Максимальное число дополнительных человеко-часов можно определить, решив систему ограничений, линии которых пересекаются в точке С. Ее решением являются х = 10000/7 и у = 10000/7 деталей в неделю.

Число используемых в точке С человеко-часов в неделю равно 10000/7 + 2 (10000/7) = 4285,7 человеко-часов в неделю. Это значение на 285,7 человеко-часов превосходит первоначальное максимальное значение 4000 человеко-часов. Получение максимального сверхнормативного запаса в 285,7 человеко-часов в неделю целесообразно при условии, что стоимость единицы дополнительного человеко-часа не превосходит 17,50 рублей в неделю. Если сверхнормативное количество часов рабочего времени используется максимально, то новое максимальное значение еженедельного дохода составит 30 * 10000/7 + 40 * 10000/7 - дополнительная стоимость = (100000 - дополнительная стоимость) рублей в неделю.

Важно уяснить, что из дохода вычитаются только те издержки, которые не фигурируют в исходной постановке задачи. Предположим, например, что при производстве автомобильных деталей стоимость одного часа рабочего времени равна 4,00 рубля. При расчете дохода, приходящегося на единицу деталей каждого типа, бухгалтер будет использовать именно эту стоимость. Если привлекается дополнительный фонд рабочего времени, к примеру, сверхурочная работа, по 6,00 рублей за 1 человеко-часов, то из них 4,00 рубля уже учтены в показателях единичного дохода. Отдельно в счет нужно внести только дополнительные 2 рубля за час.

Воздействие на оптимальное решение изменений в обеспечении нелимитирующими ресурсами

Ограничения, не являющиеся лимитирующими:

- производственные мощности для выпуска деталей типа X;

- производственные мощности для выпуска деталей типа Y;

- металлические стержни;

- постоянные заказы;

- профсоюзное соглашение.

Что происходит при изменении каждого из этих ограничений? Первые три ресурса используются в меньших или равных максимальному количествах. Любое увеличение запаса этих ресурсов не будет оказывать влияния на оптимальное решение задачи. Однако на него может влиять уменьшение запасов, соответствующих трем указанным ограничениям. Увеличение жесткости одного из нелимитирующих ограничений приведет к перемещению его линии в сторону начала координат. Сначала единственным изменением будет сокращение размеров допустимого множества. Однако когда линия ограничения переместится ниже исходной оптимальной крайней точки, данное ограничение станет лимитирующим, что приведет к появлению нового оптимального решения.

Предельные значения для этих ограничений ниже максимального уровня. Так, производственные мощности для деталей типа Х можно сократить с 2250 до 1500 часов, т.е. на 750 часов, прежде чем это ограничение начнет оказывать воздействие на решение задачи. Производственные мощности для деталей типа У могут быть сокращены с 1750 до 1250 часов, т.е. на 500 часов. Запас металлических стержней можно уменьшить с 10000 до 9250 кг, т.е. на 750 кг в неделю. Количественные выражения этих сокращений есть не что иное, как значения остаточных переменных, о которых мы упоминали выше. С ограничениями, для которых количество ресурсов больше либо равно минимальному, все наоборот. Любое сокращение минимального количества ресурсов приведет к увеличению размеров допустимого множества, но не окажет воздействия на оптимальное решение.

Любое увеличение правой части этих ограничений сначала приведет к сокращению размеров допустимого множества, а затем повлияет и на оптимальное решение. Если постоянные заказы на детали типа Х возрастут на 900 и достигнут 1500 деталей в неделю, оптимальное решение начнет изменяться. Если предусмотренное профсоюзным соглашением число деталей возрастет не менее чем на 1250 и превысит 2750 деталей, допустимое множество станет пустым, и задача не будет иметь решения. Количественные выражения увеличения ресурсов - это значения избыточных переменных для этих ресурсов, о которых говорилось выше.

Воздействие на оптимальное решение изменений в коэффициентах целевой функции

Если цель состоит в максимизации еженедельного дохода, то изменение стоимости сырья приведет к изменению значений коэффициентов целевой функции.

Пример 5. Обратимся к примерам 1 и 3. Допустимое множество изображено на рисунке А.3:

Рисунок А.3 - Задача линейного программирования для производства деталей типа Х и У в неделю

На рисунке А.3 линия дохода проходит через оптимальную крайнюю точку А.

Решение

Перепишем уравнение дохода за неделю в следующем виде:

Р = ax + 40 у (А.29)

где а — единичный доход от выпуска деталей типа X. Преобразовав это уравнение, получим:

у = Р/40 - (а/40)х (А.30)

Тангенс угла наклона линии дохода за неделю равен - (а/40). В исходном положении при а = 30 тангенс угла наклона равен - (30/40) = (3/4). Это наглядно изображено на рисунке А.4.

Рисунок А.4 - Уменьшение дохода от выпуска деталей типа Х

Если а меньше 30, то наклон линии еженедельного дохода становится более пологим. В точке А линия уровня будет отклоняться в сторону лимитирующего ограничения на фонд рабочего времени. Это ведет к уменьшению оптимального значения функции Р, дохода за неделю. Если сильно уменьшать значение параметра а, то линия уровня еженедельного дохода совпадет с ограничением на фонд рабочего времени. Это показано на рисунок А.5.

Если и далее уменьшать значение параметра а, оптимум переместится из точки А в точку D, это видно на рисунке А.6. Следовательно, граничным является положение линии уровня дохода, при котором она совпадает с линией лимитирующего ограничения на фонд рабочего времени. Этому положению соответствует наименьшее значение а, для которого А является оптимальной крайней точкой.

Рисунок А.5 - Граничное положение линии дохода по мере его уменьшения

Рисунок А.6 - Влияние дальнейшего сокращения дохода от выпуска деталей типа

Угол наклона линии ограничения на фонд рабочего времени можно найти, преобразовав данное ограничение к виду:

у = 4000/2-1/2 х (А.31)

Тангенс угла наклона лимитирующего ограничения равен - (1/2). Нижний предел значений находится из условия - (а/40) = - (1/2), таким образом, а = 20. Следовательно, единичный доход от выпуска деталей типа Х может уменьшаться до 20 рублей до того, как оптимум переместится из точки А в точку D.

Причем оптимальный доход будет сокращаться, но оптимальный ассортиментный набор не изменится до тех пор, пока значение параметра а не опустится ниже 20 рублей. Аналогичным образом можно найти верхний предел значений а. С увеличением значения а линия еженедельного дохода становится все менее пологой и в конечном итоге окажется параллельной линии другого лимитирующего ограничения, а именно на листовой металл. Любое дальнейшее увеличение значения а вызовет изменение оптимальной крайней точки и перемещение ее в точку Е. Это показано на рисунках А.7 и А.8.

Рисунок А.7 - Увеличение дохода от выпуска деталей типа Х

Рисунок А.8 - Воздействие увеличения дохода от выпуска деталей типа Х после прохождения линией уровня ее лимитирующего положения

Граничное положение линии уровня еженедельного дохода достигается в момент ее совпадения с ограничением на листовой металл. Этому положению соответствует верхний предел значений параметра а, для которых точка А является оптимальной крайней точкой допустимого множества. Угол наклона ограничения на листовой металл можно найти, преобразовав это уравнение к виду:

у = 10000/2 - (5/2)х (А.32)

Тангенс угла наклона лимитирующего ограничения равен - (5/2), а верхний предел параметра а находятся из условия - (а/40) = - (5/2), следовательно, а = 100. Таким образом, до того как оптимальный ассортиментный набор переместится из точки А в точку Е, единичный доход от выпуска деталей типа Х может возрастать до 100 рублей.

Два соответствующих предела значения единичного дохода от выпуска деталей типа Y можно найти аналогичным образом, если в изложенной схеме расчетов заменить х на у. Предположим, что значение коэффициента целевой функции при х является неизменным, тогда:

Р = 30 х + b у (А.33)

и

х = Р/30 - (b/30)у (А.34)

По мере увеличения или уменьшения параметра b граничные положения линии уровня еженедельного дохода определяются теми же двумя ограничениями, что и в предыдущем случае. Теперь необходимо записать уравнения этих ограничений так, чтобы х выступал в качестве зависимой переменной:

Фонд рабочего времени:

х = 4000 - 2у (А.35)

Тангенс угла наклона равен -2, следовательно, предельное значение достигается при условии - (b/30) = -2, т.е. b = 60.

Листовой металл:

х = 10000/5 - (2/5) (А.36)

Тангенс угла наклона равен -(2/5), для предельного значения выполняется условие: -(b/30) = -(2/5), следовательно, b = 12.

Крайняя точка А соответствует оптимальному ассортиментному набору только до тех пор, пока доход от выпуска деталей типа Y изменяется в пределах от 12 до 60 рублей за единицу. В случае если показатели единичных доходов от выпуска деталей типа Х или Y будут изменяться по сравнению с их исходными значениями, значение оптимального дохода также будет отличным от 95000 рублей.

Рассмотрим задачу, число переменных в которой больше двух. Общая схема формулировки и в этом случае остается неизменной.

Пример 2. Завод по производству электронного оборудования выпускает персональные компьютеры и системы подготовки текстов. В настоящее время освоены четыре модели:

- "юпитер" (объем памяти 512 Кбайт, одинарный дисковод);

- "венера" (объем памяти 512 Кбайт, двойной дисковод);

- "марс" (объем памяти 640 Кбайт, двойной дисковод);

- "сатурн" (объем памяти 640 Кбайт, жесткий диск).

В производственный процесс вовлечены три цеха завода — цех узловой сборки, сборочный и испытательный. Распределение времени, требуемого для обработки каждой модели в каждом цехе, а также максимальные производственные мощности цехов приведены в таблице А.1. Отдел исследований рынка производит периодическую оценку потребительского спроса на каждую модель. Максимальные прогнозные значения спроса и доходы от реализации единицы продукции каждой модели также содержатся в таблице А.1.

Построить задачу линейного программирования для изложенной проблемы производства изделий в ассортименте, если цель состоит в максимизации общегоежемесячного дохода.

Решение.

Шаг 1. Выбор переменных. Производится:

- j единиц "Юпитера" в месяц;

- v единиц "Венеры" в месяц;

- m единиц "Марса" в месяц;

- s единиц "Сатурна" в месяц.

Таблица А.1 - Время, требуемое на обработку каждой модели в каждом цехе

Цех	Время на единицу продукции	Максимальная производительность, ч/мес.
	“Юпитер”	“Венера”	“Марс”	“Сатурн”
Узловой сборки Сборочный Испытательный	0,1	0,2
Максимальное прогнозное значение спроса за месяц
Доход, руб.

Шаг 2. Цель состоит в максимизации общего дохода за месяц. Объем производства ограничен размером фонда рабочего времени по каждому цеху и возможностью продажи компьютеров каждой модели.

Шаг 3. Целевая функция задачи. Пусть Р — общий доход в месяц, тогда:

Р = 15 j + 30 v + 120 m + 130 s (А.10)

Шаг 4. Для каждого цеха время, требуемое для производства j, v, m их единиц продукции соответствующих моделей увязывается с максимальной производственной мощностью данного цеха.

Цех узловой сборки:

5j + 8v +20m+25s 800 (А.11)

Сборочный цех:

2j + 3v + 8m+14s 420 (А.12)

Испытательный цех:

0,1 j + 0,2 v+2m+4s 150 (А.13)

Спрос на "Юпитер":

j 100 (А.14)

Спрос на "Венеру":

v 45 (А.15)

Спрос на "Марс":

m 25 (А.16)

Спрос на "Сатурн":

s 20 (А.17)

Условие неотрицательности:

j, v, m, s 0 (А.18)

Литература:

1 Таха, Хемди А. Введение в исследование операций, 7-е издание.: Пер. с англ. — М.: Издатель­ский дом "Вильяме". 2005. — 912 с.

2 Моисеев Н.Н. Математические задачи системного анализа. — М.: Наука, 1981. — 488 с.

3 Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении: Учебное пособие / Под ред. А.А. Емельянова. — М.: Финансы и статистика, 2002. — 368 с.

«Транспортные задачи»

Цель: научиться решать транспортные задачи.

Задача: решить задачу согласно своему варианту.

Ход работы:

Транспортную задачу можно решить методом северо-западного угла, а так же методом потенциалов. Рассмотрим пример решения транспортной задачи для заполнения последовательности действий методом северо-западного угла.

Задача: Имеется 4 склада содержащие некоторое количество единиц однотипной продукции, имеется также 6 потребителей нуждающихся в определенном количестве данной продукции. При перевозке одной единицы продукции со склада i потребителю j возникают издержки Pij. Величины издержек приведены в таблице. При перевозке K единиц продукции со склада i потребителю j суммарные затраты на перевозку составляют K*Pij.

Требуется найти такой план перевозок при котором общие затраты на перевозку всей продукции, по всем потребителям, будут минимальны.

 

Склад №	Запас ед. продукции

 

Потребитель №	Потребность в ед. продукции

Дата добавления: 2017-02-01