Теория систем скользящих векторов и её применение в статике.

Физические величины, описывающие в механике движения, разветвление и взаимодействие относится к таким типам:

1. Скалярные величины (скаляр);

2. Векторные величины (векторы);

3. Тензорные величины (тензоры)

Скаляр можно рассматривать как тензоры нулевого порядка, нулевого порядка. А собственно тензоры-это от второго порядка и выше.

Если n- это порядок тензора, то для описания тензора n-го порядка в общем случае необходимы величины. Они могут быть как постоянными, так и переменными.

Таким образом, для описания скалярной величины необходимо одно число, либо одна переменная. Примеры скалярныхвеличин в механике: масса, расстояние, угол поворота. Геометрический образ таких величин точна.

Для описания векторной величины (в классической механики) необходимы числа или переменных (в виде вектора). Примеры векторных величин в механике: перемещение, скорость, ускорение, угловые скорость и ускорение, конечно ж – сила.

Геометрическим образом векторной величины является, которая имеет длину (модуль) и направление.

Для описания тензора 2-го порядка необходимы величин (в виде матрицы 3х3). Примером тензорных величин в механике: тензор инерции, тензор напряжения и тензор деформаций изотронного упругого тела. Геометрический образ такого тензора- трёхосный эллипсонд. Тензоры более высоких порядка в курсе рассматриваться не будут.

Вернёмся к векторам. В механике используются вектора трёх типов: свободные скалярные и связанные.

Свободные вектора можно переносить параллельно самим себе без нарушения состояния механической системы. В частности, их можно привести к началу координат или к какой-либо другой точке пространства. Это- «обычные» вектора, изучаемые в векторной алгебре. С операциями сложения, вычитания, скалярного и векторного умножения.

Скользящие вектора можно переносить только вдоль линии их действия. А параллельный перенос требует для сохранения эквивалентности состояний выполнить дополнительные операции. Которые рассмотрел ниже. В статике используются скользящие вектора. И в других разделах механики абсолютно твердого тела тоже.

Действительно (рис. 1), если к телу, находящему в равновесии приложить силу 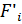, то оно начнёт вращаться по часовой стрелке.

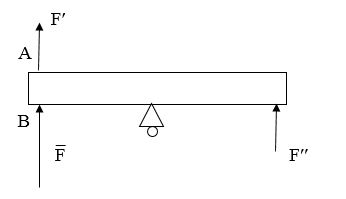
Рисунок 1

Это движение сохраняется если силу (вектор) перенести по направлению её действия (F̅ʹ). Но если силу F̅ перенести параллельно самой себе в точку С (сила Fʹʹ), то тело начнёт вращаться вокруг точки О уже против часовой стрелки.

Наконец, связаные векторы нельзя «просто так» оторвать от точки их положения, нельзя смещать вдоль направлении их действия, тем более-нельзя переносить параллельно самим себе. Такие векторы используются в механике деформируемого твердого тела (смотрите рис. 2)

F̅ F̅

а) стержень сжат б) стержень растянут

Рисунок 2

В статике изучается равновесие абсолютно твердых тел. Поэтому Вернёмся к скользящим векторам. Из рассмотренной теории (алгебры) систем скользящих векторов можно «комнатно» получить общие условие равновесия и все их частные случаи.

Рассмотрим произвольную систему сил (сила-это вектор), действующих на некоторые абсолютно твердое тело (рис. 3).

Выберем в пространстве некоторою точку О, которая называется «полюс».

o o

Рисунок 3 Рисунок 4

Примечание. Точка О (полюс) может быть выбрана в теории произвольно как внутри тела, так и вне его. Но для решения задачи всегда полезно выбирать полюс рационально, «с умом». Это очень упрощает решение. Поясним на примерах позже.

Введём две основные характеристики системы сил, рассматриваемых как система скользящих векторов.

1. Главный вектор-это векторная сума всех сил (по правилу сложению свободных векторов).

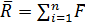(1)

Здесь n-количество сил в системе;

- все силы как активные, так и реакции опор.

Главный вектор не зависит от выбора точки О, поэтому его начало может быть перемещено в любую точку, в том числе- и в О. Размерность главного вектора системы сил: [Н]= [ ].

2. Главный момент системных сил. Вначале введём определение момента силы относительно полюса. Выберем на линии действия силы некоторою точку 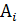. Пусть -радиус вектора с началом в полюсе О и концом в точке 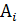. Моментом силы (либо другой векторной величины) относительно полюса называется векторное произведение радиуса-вектора на эту силу.

()= * (2)

Момент — силы-это вектор, его величина и направление из-за свойств векторного произведение не зависит от выбора точка А. Но зависит от выбора полюса О. размерность момента силы: [Н]=[ ]. Заметим, что она совпадает с размерностью энергии и работы-скалярные величины.

Модуль момента силы:

()|= * * = * (3)

Здесь L-угол между векторами.

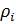- расстояние между полюсами О и линией действия силы (длина перпендикуляра, опущенного из О на линию действия ).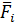

Теперь мы можем дать определение.

Главный момент системы сил относительно полюса О-это векторная сума моментов всех сил относительно этого полюса.

(4)

Поскольку каждые слагаемое в (4) зависит от выбора полюса О, то и сума,-главный момент,-зависит от выбора О.

Теория системы скользящих векторов- это несколько теорем, которые мы сейчас рассмотрим и следствия из них, (Заметим, что эта теория применима не только в статике, где вектора-это силы, но и в других разделах механики, физики, где величины-это скользящие вектора).

Теорема 1. Главный момент системы векторов относительно нового полюса равен суме «старого» главного полюса относительно полюса О и момента главного момента относительно нового полюса в предположении что главный вектор придёт в «старом» полюсе:

+ () (5)

Следствие 1. Если R=0, то главный момент не зависит от выбора полюса, =М.

Следствие 2. Две системы векторов с одинаковым главный моментом относительно какого-либо полюса, имеют одинаковые моменты относительно любого полюса тогда и только тогда, когда эти системы имеют одинаковый главный вектор.

Теорема 2. Если через полюса О и провести прямую U, то проекции главных моментов на эту прямую равны.

Главный момент системы относительно оси и называется проекция на ось главного момента системы, относительно любой точки О, взятой на этой оси U.

Теорема 3. Скалярное произведение главного момента системы на ее главный вектор не зависит от выбора полюса.

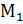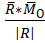| |= = – не зависит от выбора

полюса, а меняется только за счёт .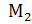

Теорема 4. Для любой системы векторов R̅≠0 всегда существует прямая и при том единственная, в точках которая = , она параллельны R̅ это-ось минимальных моментов или центральная ось системы векторов.

Векторный ноль-это система из двух векторов, равных по величине, противоположно параллельных вдоль одной прямой. Множество систем скользящих векторов: две системы эквивалентны, если одна переходит в другую путём добавлении или отбрасывание векторных нулей.

Системы скользящих векторов называется пучком, если линии их действий проходит через одну точку. Элементарное преобразование: ± векторный ноль, замены нуля одним вектором.

Теорема 5. Элементарное преобразование не меняют ни главного вектора, ни главного момента.

Для пучка скользящих векторов момент главного вектора равен главному моменту систем. Система скользящих векторов обращают пучок всегда эквивалентна одному вектору. Не образующий пучок лишь в частных случаях. Но всегда справедлива.

Теорема 6. Любая система скользящих векторов эквивалентна двум векторам, один из которых проходит через произвольно заданную точку.

Теорема 7. Для эквивалентности двух ССВ необходимо и достаточную, чтобы эти системы имели равные главные вектора и равные главные моменты относительно произвольного полюса.

Простейшие ССВ-их всего 4:

1. Система, состоящая из одного вектора;

2. Система из двух векторов, образный векторный ноль;

3. Система из двух равных и противоположных направлению векторов-пара (вектора не лежат на одной прямой);

4. Система из трёх векторов, 2 образуют пару, а линия действия третьего перпендикулярна плоска пары, эта ССВ называется винтом или динамой.

Теорема 8- основная в ССВ.

Произвольная система скользящих векторов эквивалентна из простейших.

1) - подкласс: R̅≠0 и ≠0-эквивалентна винту;

2) -подкласс: R̅=0 и ≠0- эквивалентна паре;

3) - подкласс: R̅≠0 и =0- эквивалентна вектору;

4) -подкласс: R̅=0 и =0- эквивалентна векторному нулю.

Класс	R	М	R*	Относится к
Первый	R̅≠0	≠0	R̅*	винту
Второй	R̅=0	≠0	R̅* =0	паре
Третий	R̅≠0	=0	R̅* =0	вектору
Четвёртый	R̅=0	=0	R̅* =0	векторному нулю

Здесь -составляющая главного момента (О не центр оси), параллельная главному вектору R̅, M̅-главный момент относительно произвольной точки, не зависит от выбора полюса.

В третьем случаи вектор называется равнодействующим, он совпадает с главным вектором, а линия его действия служит центральной осью.

+ ()= (

Второй-подкласс: множество эквивалентно пар плечо пары, молот пары.

Четвёртый – динама можно заменить пару эквивалентную.

Наконец, первый –он относится к системе.

Системы, эквивалентны первому подклассу называется уравновешенными.

R̅=0; =0: (точка О-произвольная)

Это-векторные уравнения равновесия.

В проекциях на оси эти уравнения принимают вид:

∑ =0 =∑ ()=0

∑ =0 =∑ ()=0

∑ =0 =∑ ()=0

Векторных уравнений равновесия в статике-2, а в частных случаях эквивалентных им скалярных-6.

1. Пучок

R̅=0

∑ =0

∑ =0

∑ =0

2. Плоская система сил

∑ =0 ∑ ()=0

∑ =0

3. Система параллельных сил

∑ =0 ∑ ()=0

∑ ()=0

4. Произвольная система пар

∑ ()=0

∑ ()=0

∑ ()=0

Дата добавления: 2017-02-01