Полиномы Баттерворта

Биноминальные полиномы (Полиномы Ньютона)

Задача максимального быстродействия. Колебательный объект 2 порядка

Задача максимального быстродействия. Объект 3 порядка

Принцип максимума Понтрягина. Линейная квадратичная задача.

Рассматриваемая задача заключается в том, чтобы перевести объект управления из начального состояния в конечное таким образом, чтобы минимизировать функционал вида:

Особенностью линейной квадратичной задачи является то, что соответствующее управляющее воздействие может быть получено не только в виде функции времени, но и виде линейной функции состояний объекта управления.

Рассмотрим решения задачи на примере.

Требуется найти управляющее воздействие, переводящее объект управления

(6.1)

из состояния

в состояние

таким образом, чтобы обеспечить минимум следующего функционала

(6.2)

Решение задачи находится путем выполнения стандартных шагов.

Гамильтониан

Исходя из максимизации Гамильтониана, находим оптимальное управление в функции сопряженных переменных

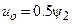
Система сопряженных уравнений

Общая система уравнений, среди решения которой находится искомое управление

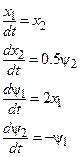(6.3)

Для решения полученной системы уравнений применим метод преобразования Лапласа. Следует отметить, что при записи преобразованной по Лапласу системы уравнений необходимо ввести в рассмотрение значения начальных условий для переменных сопряженной системы уравнений. Эти начальные условия первоначально неизвестны, но будут определены позднее исходя из обеспечения заданных конечных условий для объекта управления.

Преобразованная по Лапласу система уравнений имеет вид

(6.4)

Поскольку 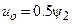, для определения L-изображения управления необходимо найти решение последней системы уравнений относительно .

В соответствии с правилом Крамера можно записать

где

Анализируя полученное выражение для (точнее ) можно заметить, что выражение для во временной области будет содержать 4 экспоненты, две из них будут иметь положительные степени, а другие две – отрицательные. Очевидно, что наличие возрастающих экспонент не позволить получить конечное значение критерия качества (6.2) и противоречит заданным конечным условиям для 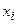, следовательно, из всех решений системы уравнений (6.3) необходимо выбрать те, у которых постоянные интегрирования обеспечивают равенство нулю коэффициентов перед возрастающими экспонентами. Это условие вполне может быть выполнено за счет соответствующего вычисления .

Запишем решение системы уравнений (6.4) выделив составляющие, соответствующие затухающим и возрастающим экспонентам во временной области.

(6.5)

Неизвестные коэффициенты определяются из условия равенства соответствующих полиномов в выражении (6.5)

(6.6)

Из условия равенства полиномов (6.6) следует равенство коэффициентов при одинаковых степенях в этих полиномомах.

Полученные выражения показывают, что для подавления возрастающих экспонент необходимо выбрать начальные условия для сопряженных переменных следующим образом:

(6.7)

или

(6.8)

Исключение неизвестных из уравнений (6.8) позволяет получить следующую систему уравнений для начальных условий для сопряженных переменных:

При этом постоянные интегрирования примут следующие значения:

(6.8)

Полученные соотношения уже позволяют получить выражение для управления как функции времени на основе обратного преобразования (6.4) по Лапласу.

Для получения управления с обратными связями необходимо выполнить следующую работу:

- получить L-изображение управляющего воздействия для объекта управления замкнутого пока неизвестными обратными связями;

- составить систему уравнений для определения неизвестных коэффициентов обратной связи путем приравнивания выражения для L-изображения управляющего воздействия замкнутого объекта управления и выражения для оптимального управления, полученного на основе (6.5).

Рассмотрим эти операции применительно к рассматриваемому примеру.

Уравнения замкнутого объект управления получаются из (6.1) в предположении, что

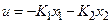
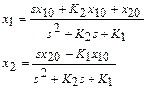
(6.9)

Определение коэффициентов обратной связи выполняется на основании выражений (6.5), (6.7), (6.9) и (6.8)

Индивидуальные задания (по бригадам)

По каждому варианту необходимо получить аналитические выражения для оптимального управления как функции времени и оптимальные значения для коэффициентов обратной связи, а также построить графики переходных процессов в оптимальной системе (, , )

Для всех вариантов граничные значения состояний объекта управления .

Вариант (№ бригады)	Объект управления

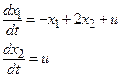
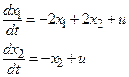
Решение задач управления по критерию максимального быстродействия резко усложняется с повышением порядка дифференциальных уравнений, описывающих объект управления.

Основным методом решения задачи максимального быстродействия для объектов, описываемых дифференциальными уравнениями выше второго порядка, является поиск моментов переключения.

Для случая объекта 3 порядка, собственные числа которого являются вещественными числами, задача поиска может быть сформулирована следующим образом:

Требуется найти такие значения параметров , и , где и моменты переключения знака управляющего воздействия, а - момент выключения управления, при которых расстояние между изображающей точкой, соответствующей моменту и требуемым конечным состоянием объекта, было бы минимальным. Практика выполнения расчетов показывает, что зависимость точности обеспечения заданных конечных условий от набора моментов переключения носит очень сложный характер и содержит большое количество локальных экстремумов. В таких условиях существенно возрастает значение выбора начальной точки поиска.

Одним из возможных способов определения начальной точки поиска является решение промежуточной задачи максимального быстродействия для усеченного объекта 2 порядка.

Более подробно процесс решения задачи максимального быстродействия для объекта 3 порядка рассмотрим на следующем примере.

Допустим, что объект управления описывается следующими уравнениями:

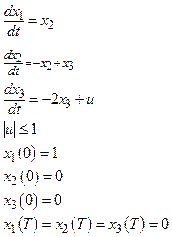
где , , - состояния объекта управления, - управляющее воздействие, - момент времени перевода объекта в конечное состояние.

Очевидно, что собственные числа рассматриваемого объекта являются вещественными, следовательно, в соответствии с теоремой об интервалах, для управления этим объектом управляющее воздействие должно быть максимально по модулю и менять знак 2 раза.

Очевидно, также, что оптимальной траектории с заданными граничными условиями на плоскости соответствует замкнутая кривая, на которой находятся две точки переключения.

На первом этапе решения задачи выберем первую точку переключения произвольно (). При выбранном значении момент второго переключения и момент выключения управления могут быть однозначно определены с помощью построения линии переключения в плоскости методом обратного времени.

Поскольку момент был выбран произвольно конечное состояние объекта управления по состоянию будет отличаться от заданного. Обозначим его .

Таким образом, мы получили набор моментов переключения, который обеспечивает минимальное время перевода объекта в точку промежуточного финиша: [ 0 0].

Для определения набора точек переключения, соответствующего заданным конечным условиям требуется выполнить серию поисковых расчетов, в каждом из которых в качестве начального набора точек переключения использовать результат предыдущего расчета, а точка промежуточного финиша систематически приближается к заданному конечному состоянию.

С одной стороны, увеличение скорости приближения точки промежуточного финиша к заданному положению может уменьшить потребное количество расчетов но, с другой стороны, может спровоцировать сходимость поиска к ошибочному локальному минимуму или привести к аварийному завершению процесса поиска (например, по исчерпанию лимита итераций).

Описанные выше вычисления могут быть выполнены с помощью следующих MATLAB программ:

Файл Main7.m

% Определение начальной комбинации моментов переключения

global T t1 t2

% Построение линии переключения в плоскости x2x3 c

% использованием обратного времени

[t,x]=ode45(‘Odefun7_1’,[0 5],[0 0 0]);

plot(x(:,2),x(:,3),’r’)

hold on

% Построение траектории из нач. состояния в прямом времени

t1=1;

t2=1.5;

T=2;

[t,x]=ode45(‘Odefun7_2’,[0 T],[1 0 0])

plot(x(:,2),x(:,3),’b’)

Файл Odefun7_1.m

function f=Odefun7_1(t,x)

u=-1;

f=[-(x(2));-(-x(2)+x(3));-(-2*x(3)+u)];

Файл Odefun7_2.m

function f=Odefun7_1(t,x)

global t1 t2

if t<t1

u=-1;

elseif t<t2

u=1

else

u=-1

end

if t>T

u=0;

end

f=[x(2);(-x(2)+x(3));(-2*x(3)+u)];

Выполненные с помощью программы расчеты показали, что набор моментов переключения позволяет перевести объект в точку промежуточного финиша с координатами

Полученный набор точек переключения и координаты точки промежуточного финиша использовались для уточнения набора точек переключения и координат точки промежуточного финиша методом поиска, реализованного в следующей программе.

Файл Main7_2.m

t0=[1 1.85 2.1]

T=fminsearch(‘fmsfun7_2_1’,t0)

Файл fmsfun7_2_1

function f=fmsfun7_2_1(T)

global TT x

TT = T;

[t,x]=ode45('odefun7_2_1',[0 T(3)],[1 0 0]);

xf=[0.78 0 0];

f=(x(length(t),1)-xf(1))^2+(x(length(t),2)-xf(2))^2+(x(length(t),3)-xf(3))^2;

% plot(x(:,2),x(:,3),'b')

plot(t,x)

pause(0.1)

Файл odefun7_2_1

function f=odefun7_2_1(t,x)

global TT

if t<TT(1)

u=-1;

elseif t<TT(2)

u=1

else

u=1

end

if t>TT(3)

u=0;

end

f=[x(2);-x(2)+x(3);-2*x(3)+u];

Программа Main7_2.m позволила получить хорошие результаты всего за два шага.

На первом шаге использовался набор точек переключения и точка промежуточного финиша . Результатом работы программы был уточненный набор точек переключения .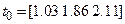

На втором шаге использовался набор точек переключения, полученный на первом шаге, и новые координаты точки промежуточного финиша . В результате второго шага получен набор точек переключения , обеспечивающий перевод объекта в конечную точку с приемлемой точностью.

Индивидуальные задания (по бригадам)

По каждому варианту необходимо определить набор моментов переключения знака управляющего воздействия, который необходим для перевода объекта из состояния [10 0 0] в состояние [0 0 0] а также определить момент выключения управления.

Модуль управляющего воздействия не может превосходить 1.

Кроме определения моментов переключения необходимо построить графики зависимости состояний объекта и управления от времени, соответствующие оптимальному переходу из начального состояния в конечное.

Вариант (№ бригады)	Объект управления

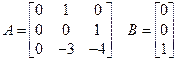
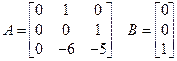
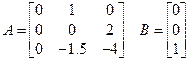
Особенностью оптимального по быстродействию управления колебательными объектами является то, что на эти объекты не распространяется теорема об N интервалах.

Другими словами, количество переключений зависит не только от порядка дифференциальных уравнений, но и от взаимного положения заданных начального и конечного состояний объекта управления.

Подтверждение этой особенности управления колебательными объектами можно получить на основе принципа максимума.

В соответствии с этим принципом оптимальное управляющее воздействие зависит от сопряженных переменных следующим образом:

U0=sign(F(ksi1, ksi2, …))

Кроме того, известно, что в случае колебательных объектов управления сопряженные переменные, как функции времени, содержат гармонические составляющие, частоты которых равны частотам свободных колебаний объекта управления.

Следовательно, по отношению к колебательным объектам 2 порядка принцип максимума позволяет сделать следующие выводы:

- количество переключений знака управляющего воздействия может быть больше 1;

- оптимальные по быстродействию траектории состоят из нескольких фрагментов, время движения по каждому из которых не может превышать половину периода свободных колебаний объекта управления.

Построение оптимальных траекторий рассмотрим на примере консервативного колебательного звена 2 порядка.

Задаче максимального быстродействия для приведенного выше объекта управления соответствует следующий гамильтониан

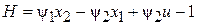
Очевидно, что оптимальное управление зависит от сопряженных переменных следующим образом

Система сопряженных уравнений

Поскольку уравнения относительно сопряженных переменных не зависят от состояний объекта, выражение для может быть найдено из решения только системы сопряженных уравнений

(8.1)

Полученное выражение для показывает, что управляющее воздействие может иметь неограниченное количество переключений знака, но интервал постоянства знака не может превышать секунд.

Для определения оптимальных моментов переключения можно использовать графический метод построения линий переключения в фазовом пространстве.

На первом этапе построим фрагмент линии переключения первого порядка, который является траекторией движения объекта управления, приводящей его к конечному состоянию под действием постоянного управления. Эта операция может быть выполнена путем записи фазовой траектории движения объекта в обратном времени из заданного конечного состояния. Как следует из (8.1) длительность этого фрагмента не может превышать секунд. Фрагмент линии переключения второго порядка, который соответствует второму переключению в обратном времени (или предпоследнему переключению в прямом времени) можно построить как некоторое геометрическое место точек. Это геометрическое место точек образуется концами траекторий длительностью секунд, начинающихся в обратном времени на фрагменте первого порядка. Очевидно, что для перехода от фрагмента первого порядка к фрагменту второго порядка необходимо переключить знак управления. Аналогичным образом могут быть построены фрагменты линии переключения следующих порядков.

Описанный выше алгоритм построения линии переключения реализован в следующей MATLAB программе.

В процессе выполнения расчетов оказалось, что солвер ode23s выполняет численное решение рассматриваемых дифференциальных уравнений гораздо точнее, чем солвер ode45

Файл Test8.m

%Построение фрагмента линии переключения первого порядка

% для положительного управления в обратном времени

[t,x]=ode45('odefun8',[0 pi],[0 0]);

plot(x(:,1),x(:,2),'r')

hold on

%Генерация координат точек фрагмента линии переключения второго

% порядка

%Искомые координаты вычисляются как координаты концов набора

% траекторий, исходящих в обратном времени из фрагмента линии

% переключения первого порядка под действием отрицательного управления

%N - количество генерируемых точек

global i N

N=20;

t=[];

x=[];

x1g=[];

x2g=[];

for i=1:N

[t,x]=ode23s('odefun8_2',[0 pi*(i/N+1)],[0 0]);

%Упаковка координат точек фрагмента второго порядка в отдельные

% массивы

x1g=[x1g x(length(t),1)];

x2g=[x2g x(length(t),2)];

end

plot(x1g,x2g,'r')

%За счет применения команды hold on настоящая программа отображает

% фрагменты линии переключения первого и второго порядков

%Программа обеспечения поиска моментов переключения переводящих

% объект из точки [-1 -4] в точку [0 0]

%программа помогает выполнять ручной поиск моментов

% переключения/отключения (t1, t2, T), ориентируясь на графики фрагментов

% линии переключения

global t1 t2 T

t1=1.32;

t2=4.46;

T=6.5;

t=[];

x=[];

[t,x]=ode23s('odefun8_3',[0 T],[-1 -4]);

plot(x(:,1),x(:,2),'b')

Файл odefun8.m

function f=odefun8(t,x)

f=[-(x(2));-(-x(1)+1)];

Файл odefun8_2.m

function f=odefun8_2(t,x)

global i N

if t<=i*pi/N

u=1;

else

u=-1;

end

f=[-(x(2));-(-x(1)+u)];

Файл odefun8_3.m

function f=odefun8_3(t,x)

global t1 t2 T

if t<t1;

u=1;

elseif t<t2;

u=-1;

else

u=1;

end

if t>T

u=0;

end

f=[(x(2));(-x(1)+u)];

С помощью приведенной выше программы были получены следующие параметры оптимального прцесса:

сек., сек. и сек.

Фазовая траектория оптимального процесса и графики фрагментов линии переключения показаны на рис. 8.1

Рис. 8.1. Фазовая траектория оптимального процесса

Индивидуальные задания (по бригадам)

По каждому варианту необходимо определить набор моментов переключения знака управляющего воздействия, который необходим для перевода объекта из начального в конечное состояние а также определить момент выключения управления.

Модуль управляющего воздействия не может превосходить 1.

Кроме определения моментов переключения необходимо построить графики фазовой траектории оптимального процесса и графики фрагментов линии переключения.

Для всех вариантов уравнения объекта управления имеют следующий вид:

Вариант (№ бригады)	Параметры объекта управления

Приложение 1. Стандартные характеристические полиномы

Общая форма полиномов (нормирование по базовой частоте ):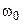

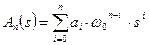
О динамических свойствах систем, имеющих рассматриваемые характеристические полиномы, можно судить по переходным характеристикам:

где - оператор обратного преобразования Лапласа.

Коэффициенты биноминального полинома степени 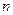приведены в таблице.

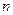
Коэффициенты полинома Баттерворта степени 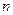приведены в таблице.

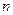
		1.4
		2.6	3.4	2.6
		3.24	5.24	5.24	3.24
		3.86	7.46	9.13	7.46	3.86
		4.5	10.1	14.6	14.6	10.1	4.5
		5.12	13.14	21.84	25.69	21.84	13.14	5.12

3. Полиномы, минимизирующие функционал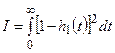

Коэффициенты рассматриваемого полинома степени 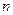приведены в таблице.

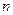
4. Полиномы, минимизирующие функционал

Коэффициенты рассматриваемого полинома степени 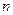приведены в таблице.

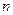
		1.4
		2.15	1.75
		2.7	3.4	2.1
		3.4	5.5		2.8
		3.95	7.45	8.60	6.60	3.25
		4.58	10.64	15.54	15.08	10.42	4.475
		5.15	13.3	22.20	25.75	21.60	12.80	5.20

Приложение 2. Контрольные вопросы

1. Что является результатом аналитического решением дифференциального уравнения?

2. Что является результатом численного решения дифференциального уравнения?

3. Сколько решений имеет дифференциальное уравнение порядка ?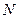

4. Приведите соответствия между оригиналами и L-изображениями основных функций, используемых при решении дифференциальных уравнений.

5. Чем отличаются статические и динамические задачи оптимизации?

6. Приведите основные особенности метода поиска, реализованного в MATLAB-функции FMINSEARCH.

7. Зависит ли результат работы функции FMINSEARCH от выбора начальной точки поиска и почему?

8. Сколько решений имеет задача поиска базовой частоты стандартного полинома, обеспечивающей минимальное время переходного процесса в линейной системе управления?

9. Как определяется время переходного процесса при решении задачи модального управления?

10. Какие этапы выполняются при решении задач оптимального управления на основе принципа максимума Л.С. Понтрягина?

11. В чем особенности применения принципа максимума Л.С. Понтрягина к решению задач на экономию управления?

12. Приведите общий вид выражения для управляющего воздействия как функции времени. (Имеется в виду задача экономии управления объектом, собственные числа которого вещественны и различны).

13. Что обычно является результатом решения задачи экономии управления численным методом на основании принципа максимума?

14. Сформулируйте задачу оптимизации расхода управления ориентированную на использование поисковых методов.

15. В чем особенности применения принципа максимума Л.С. Понтрягина к решению задач оптимального быстродействия?

16. Сформулируйте теорему об N интервалах.

17. Докажите, что теорема об N интервалах неприменима к объектам управления, собственные числа которых являются комплексными.

18. Начертите график функции времени, которая может быть решением задачи оптимального быстродействия для объекта управления 2 порядка, собственные числа которого вещественны и различны.

19. Начертите график функции времени, которая не может быть решением задачи оптимального быстродействия для объекта управления 2 порядка, собственные числа которого вещественны и различны.

20. Начертите график функции времени, которая не может быть решением задачи оптимального быстродействия для объекта управления 2 порядка, собственные числа которого являются комплексными числами.

21. Можно ли реализовать оптимальное по быстродействию управление в виде регулятора с обратными связями?

22. Что обычно является результатом решения задачи оптимального быстродействия численным методом на основании принципа максимума?

23. Сформулируйте задачу оптимального быстродействия, ориентированную на использование поисковых методов.

24. В чем особенности применения принципа максимума Л.С. Понтрягина к решению линейной квадратичной задачи?

25. Какие этапы выполнялись в процессе решения задачи оптимального быстродействия в лабораторной работе 7?

26. Опишите процесс построения линий переключения при выполнении лабораторной работы 8.

Дата добавления: 2017-02-01