Сформулюйте означення багатофакторної лінійної регресії.

На будь-який економічний показник найчастіше впливає не один, а декілька факторів. У цьому випадку замість парної регресії розглядається багатофакторна регресія:

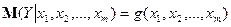                                                                     (1)

Рівняння багатофакторної регресії може бути представлене у вигляді:

                                                                                                              (2)

де  – вектор незалежних (пояснюючих) змінних;

   – вектор невідомих параметрів;

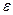                                 – випадкове відхилення;

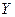                                 – залежна (пояснювана) змінна.

Розглянемо найбільш просту з моделей багатофакторної регресії – модель багатофакторної лінійної регресії.

Теоретичне лінійне рівняння багатофакторної регресії має вигляд:

        (3)

Фактичні значення залежної змінної знаходяться за формулою:

(4)

43. Сформулюйте означення парної лінійної регресії.

Функціональна залежність умовного математичного сподівання 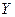 від 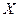 називається функцією регресії  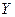на :

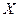                                                (1)

де  – значення В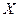В  в -му спостереженні, .

Парна лінійна регресія являє собою лінійну функцію між умовним математичним сподіванням 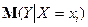залежної змінної  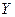і однією незалежною змінною :

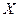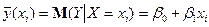.                                      (2)

Співвідношення (2) називається теоретичним лінійним рівнянням регресії. Для відображення того факту, що кожне фактичне значення залежної змінної ( ) відхиляється від відповідного умовного математичного сподівання ( ), необхідно ввести в співвідношення (2) випадковий доданок :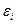

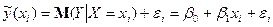,                                     (3)

де ,  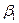– теоретичні параметри (теоретичні коефіцієнти) регресії;

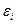        – випадкові відхилення.

Співвідношення (3) називається теоретичною лінійною регресійною моделлю. За вибіркою можна побудувати емпіричне рівняння регресії:

,                                                             (4)

де 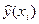 – оцінка умовного математичного сподівання ;

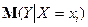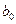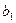,  – оцінки невідомих параметрів  (емпіричні коефіцієнти регресії).

Фактичні значення залежної змінної ( 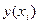) розраховуються за формулою:

,                                                      (5)

де 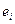 – оцінка теоретичного випадкового відхилення .

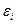44. Сформулюйте означення та наведіть формули для розрахунків SSR, SSE, SST. Ступені вільності величин SSR, SSE, SST.

SST – загальна сума квадратів яку прийнято позначати SST (sum square total)

SSE – сума квадратів помилок сума квадратів помилок, яка позначаєтьсяSSE (sum square error)

SSR – сума квадратів, що пояснюється регресією та позначаєтьсяSSR (sum square regression)

;

 ;

 .

Розглянемо тотожність, яка пов'язує загальну суму квадратів із сумою квадратів помилок та із сумою квадратів, що пояснюють регресію:

ST = SSE + SSR.

Кожна сума квадратів пов'язана з числом, яке називається її ступенем вільності, це число показує, скільки незалежних елементів інформації, які утворюються з елементів (у₁,...,у_n) потрібно для розрахунку даної суми квадратів.

Розглянемо, скільки ступенів вільності має кожна, вивчена нами сума квадратів.

Для утворення SSTпотрібно(n -1) незалежних чисел, тому що з чисел

{(y₁ - ), (y₂ -), ... , (y_n -)}незалежні тільки (n -1) завдяки властивості:

Сума квадратів, що пояснює регресію - SSR має тільки єдину незалежну одиницю інформації, яка утворюється з у₁,...,у_n, а саме b₁. Доведемо це.

Запишемо відхилення, що пояснює регресію, у вигляді:

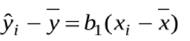
Візьмемо суми з обох боків рівняння і піднесемо їх до квадрату:

Таким чином, дійсно SSR можна утворити, використовуючи лише єдину незалежну одиницю інформації b₁.

Сума квадратів помилок SSE має (n - 2) ступеня вільності:

SST = SSE + SSR

У разі простої лінійної регресії: n-1 = n-2 + 1

Ця сума базується на кількості ступенів вільності, яка дорівнює різниці між кількістю спостережень і кількістю параметрів, що оцінюються. У разі простої лінійної регресії оцінюються два параметри b₀таb₁. Якщо позначити кількість спостережень черезn, то дляSSE маємо (n- 2) ступеня вільності. Ступені віль­ності позначаються так:df або Df.

Дата добавления: 2023-11-03