
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Затухающие механические и электромагнитные колебания
|
|
|
|
3.1. Примеры решения задач
Пример 1
Амплитуда затухающих колебаний математического маятника за время 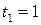 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время
мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время  мин?
мин?
Дано:
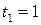 мин мин

 мин мин
|
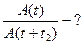
|
Решение. Амплитуда затухающих колебаний уменьшается с течением времени по закону
 ,
,
где  – амплитуда в момент времени
– амплитуда в момент времени 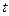 ;
;
 - амплитуда колебаний в начальный момент времени;
- амплитуда колебаний в начальный момент времени;
 - коэффициент затухания.
- коэффициент затухания.
Тогда
 и
и
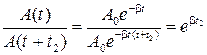 .
.
Прологарифмировав оба уравнения, выразим из каждого уравнения коэффициент затухания  :
:
 и
и  .
.
Приравнивая правые части полученных выражений, находим, что 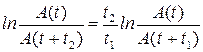 , откуда следует, что
, откуда следует, что
 .
.
 .
.
Ответ:  .
.
Пример 2.
Гиря массой  кг подвешена к пружине, жесткость которой
кг подвешена к пружине, жесткость которой  Н/м, и совершает затухающие колебания. Определить их период
Н/м, и совершает затухающие колебания. Определить их период 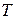 в двух случаях: 1) за время, в течении которого произошло
в двух случаях: 1) за время, в течении которого произошло  колебаний, амплитуда уменьшилась в
колебаний, амплитуда уменьшилась в  раза; 2) за время двух колебаний (
раза; 2) за время двух колебаний (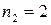 ) амплитуда колебаний уменьшилась в N2 = 20 раз.
) амплитуда колебаний уменьшилась в N2 = 20 раз.
Дано:
 кг кг
 Н/м Н/м



|


|
Решение: Сопротивление среды уменьшает частоту свободных колебаний. Период
затухающих колебаний определяется по соотношению
 .
.
Циклическую частоту собственных колебаний  определим по соотношению
определим по соотношению
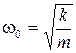
Коэффициент затухания вычислим по формуле
 .
.
Чтобы найти величину 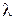 , обратимся к уравнению затухающих колебаний
, обратимся к уравнению затухающих колебаний
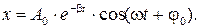
Уменьшающуюся со временем амплитуду выразим так:
 .
.
Пользуясь введенными в условии задачи обозначениями, можно записать

 .
.
Тогда
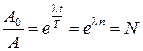 .
.
Отсюда, логарифмируя, имеем
 .
.
Подставив численные значения N и n для двух случаев, получим:
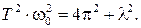
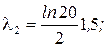
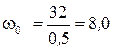
 .
.
Теперь запишем формулу для периода колебаний 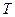 с учетом выражения для
с учетом выражения для 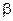
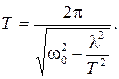
Получилось квадратное уравнение относительно 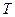 . Решая его, находим (отбросив, отрицательный корень)
. Решая его, находим (отбросив, отрицательный корень)
|
|
|
 .
.
Приступая к вычислениям периода, заметим, что в первом случае  . Поэтому, сохраняя достаточную точность вычислений, можно пренебречь слагаемым
. Поэтому, сохраняя достаточную точность вычислений, можно пренебречь слагаемым  , тогда
, тогда
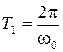 .
.
Во втором случае величину  отбросить нельзя.
отбросить нельзя.
Произведем вычисления:
 с;
с;
 с.
с.
Ответ:  с,
с,  с.
с.
Пример 3*
Математический маятник длиной  см совершает затухающие колебания. Через какое время
см совершает затухающие колебания. Через какое время  энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания:
энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания:
а)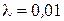 ; б)
; б)  .
.
Дано:
 см = см =  м м
 = 9,4
а) = 9,4
а) ;
б) ;
б)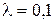 . .
|
 -? -?
|
Решение. Полная энергия маятника, совершающего затухающие колебания, уменьшается с течением времени по закону
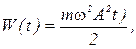
где  – масса маятника;
– масса маятника;
 - частота затухающих колебаний;
- частота затухающих колебаний;
 - амплитуда маятника в момент времени.
- амплитуда маятника в момент времени.
Тогда отношение энергии маятника  в момент времени
в момент времени 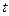 к энергии маятника
к энергии маятника  в момент времени равно
в момент времени равно
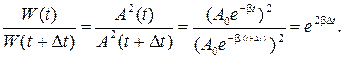
Так как  - по условию, то
- по условию, то
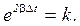
Коэффициент затухания 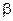 связан с логарифмическим декрементом затухания
связан с логарифмическим декрементом затухания  соотношением
соотношением
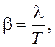
где T – период затухающих колебаний.
Таким образом,
 , откуда следует, что
, откуда следует, что
 . (1)
. (1)
Период затухающих колебаний 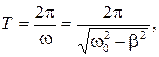
где 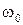
 – частота собственных колебаний маятника.
– частота собственных колебаний маятника.
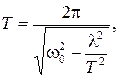
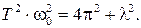
Таким образом, период затухающих колебаний равен
 (2)
(2)
Подставив формулу (2) в выражение (1) для определения времени, получим
 . (3)
. (3)
а) 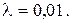
Так как  , то слагаемым
, то слагаемым  в формуле (3) можно пренебречь.
в формуле (3) можно пренебречь.
Следовательно,
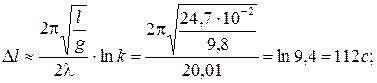
б) 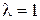
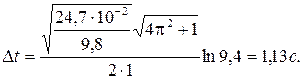
Ответ: а) l=0,01, D t =112 c; б) 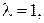
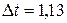 с.
с.
Пример 4*
К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на  см. Оттягивая этот груз и опуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания
см. Оттягивая этот груз и опуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания 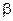 , чтобы: а) колебания прекратились через время
, чтобы: а) колебания прекратились через время  с (считать условно, что колебания прекратились, если их амплитуда упала до 1% от начальной); б) груз возвращался в положение равновесия апериодически; в) логарифмический декремент затухания колебаний был
с (считать условно, что колебания прекратились, если их амплитуда упала до 1% от начальной); б) груз возвращался в положение равновесия апериодически; в) логарифмический декремент затухания колебаний был  ?
?
Дано:
 см = см =  а)
а) t = 10с
б)
t = 10с
б) в)
в) 
|
 -? -?
|
Решение:
|
|
|
а) 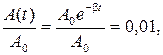
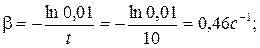
б) при возвращении груза в положение равновесия апериодически частота затухающих колебаний становится равной нулю:
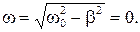
Следовательно, 
где  – частота собственных колебаний груза на пружине;
– частота собственных колебаний груза на пружине;
 - жесткость пружины;
- жесткость пружины;
 - масса груза.
- масса груза.
В состоянии равновесия на груз действует две силы: сила тяжести 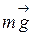 и сила упругости
и сила упругости  , причем
, причем
 ,
,
 , откуда получим, что
, откуда получим, что
 .
.
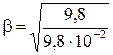
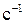 ;
;
в) 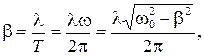
где  – частота затухающих колебаний;
– частота затухающих колебаний;
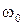 - частота собственных колебаний.
- частота собственных колебаний.
Преобразуя уравнение (1), получим для определения 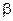 следующее выражение:
следующее выражение:
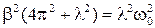 - откуда находим, что
- откуда находим, что
 .
.
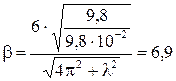
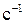 .
.
Ответ: 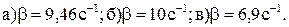
Пример 5*
Колебательный контур состоит из конденсатора емкостью 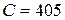 нФ, катушки с индуктивностью
нФ, катушки с индуктивностью  мГн и сопротивления
мГн и сопротивления 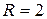 Ом. Во сколько раз уменьшится разность потенциалов на обкладках конденсатора за один период колебаний?
Ом. Во сколько раз уменьшится разность потенциалов на обкладках конденсатора за один период колебаний?
Дано:
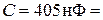  Ф Ф
  t = 10с
t = 10с
 Ом Ом
|

|
Решение: Амплитудное значение разности потенциалов, при затухающих колебаниях, уменьшается по экспоненциальному закону
 ,
,
где  – амплитуда разности потенциалов в начальный момент времени
– амплитуда разности потенциалов в начальный момент времени 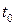 ;
;
 - коэффициент затухания.
- коэффициент затухания.
Тогда  ,
,
где 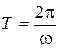 – период затухающих колебаний.
– период затухающих колебаний.
Так как частота  затухающих колебаний связана с частотой
затухающих колебаний связана с частотой  собственных колебаний соотношением
собственных колебаний соотношением  , то период затухающих колебаний вычисляется так:
, то период затухающих колебаний вычисляется так:
 .
.
Следовательно,
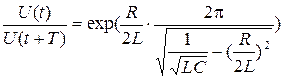 .
.
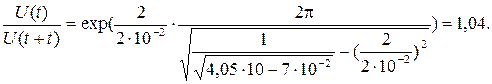
Ответ: 
Пример 6*
Колебательный контур имеет емкость  нФ и индуктивность
нФ и индуктивность  мГн. Логарифмический декремент затухания
мГн. Логарифмический декремент затухания  . За какое время вследствие затухания потеряется 99% энергии контура?
. За какое время вследствие затухания потеряется 99% энергии контура?
Дано:
 Ф Ф
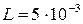 Гн Гн


|

|
Решение: Энергия колебательного контура равна максимальной энергии электрического поля в контуре, которая пропорциональна амплитуде заряда на обкладках конденсатора:
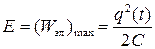 ,
,
где 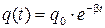 .
.
Преобразуем заданное условие  к виду:
к виду:
 ;
;
По условию задачи
 , т.е.
, т.е. 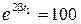
 .
.
Чтобы найти коэффициент затухания  , выразим его через логарифмический декремент затухания
, выразим его через логарифмический декремент затухания 
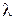 и частоту незатухающих колебаний в контуре
и частоту незатухающих колебаний в контуре 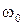
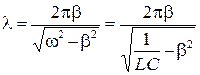 ;
;
отсюда  ;
;  ;
;
С учетом этого  .
.
Произведем вычисления:
 с
с
Ответ:  с
с
Пример 7
Гиря массой 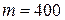 г, подвешенная на пружине жесткостью
г, подвешенная на пружине жесткостью 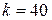 Н/м, опущена в масло. Коэффициент сопротивления
Н/м, опущена в масло. Коэффициент сопротивления  для этой системы составляет
для этой системы составляет  кг/c. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону
кг/c. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону  (Н).Определите: 1) амплитуду вынуждающих колебаний, если частота вынуждающей силы вдвое меньше частоты собственных колебаний; 2) частоту вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна; 3) резонансную амплитуду.
(Н).Определите: 1) амплитуду вынуждающих колебаний, если частота вынуждающей силы вдвое меньше частоты собственных колебаний; 2) частоту вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна; 3) резонансную амплитуду.
|
|
|
Дано:
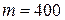 г г
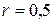 кг/с кг/с
 ,Н ,Н
 Н/м Н/м

|
1)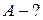 2)
2) 3)
3)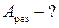
|
Решение: 1) Амплитуда вынужденных колебаний:
 ,
,
Учитывая, что  , а
, а  и
и 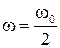 получаем
получаем
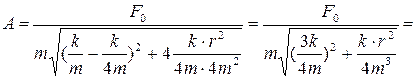
=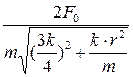
Подставляя значения, получаем
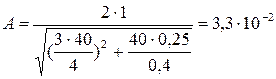 м=3,3 см
м=3,3 см
2)  с-1;
с-1;
3)  м=20 см.
м=20 см.
Ответ: 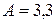 см;
см;  с-1;
с-1;  см.
см.
Пример 8.
Участок цепи, состоящий из последовательно соединенных конденсатора  Ом и активного сопротивления, подключили к внешнему переменному напряжению с амплитудой
Ом и активного сопротивления, подключили к внешнему переменному напряжению с амплитудой  В. При этом амплитуда установившегося тока оказалась равной
В. При этом амплитуда установившегося тока оказалась равной  А. Найти разность фаз между током и внешним напряжением.
А. Найти разность фаз между током и внешним напряжением.
Дано:



|
 -? -?
|
Решение: В данном случае  ,
, 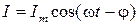 где
где 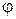 определяется по формуле (28) при
определяется по формуле (28) при  :
:
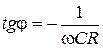 .
.
Неизвестное значение емкости 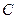 найдем из выражения для амплитуды тока
найдем из выражения для амплитуды тока
 ;
;
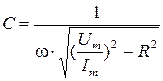 .
.
После подстановки в выражение для 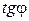 получили:
получили:
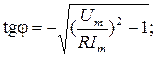
Произведем вычисления:
 ;
;
 .
.
В нашем случае, это означает, что ток опережает по фазе напряжение.
Ответ: 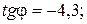
 .
.
3.2. Задачи для самостоятельного решения.
1. Амплитуда затухающих колебаний маятника за время 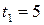 мин уменьшилась в
мин уменьшилась в  раза. За какое время
раза. За какое время  , считая от начального момента, амплитуда уменьшится в
, считая от начального момента, амплитуда уменьшится в 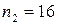 раз?
раз?
(t2=20 мин)
2. Амплитуда колебаний математического маятника длиной  м за время
м за время  мин уменьшилась в
мин уменьшилась в 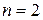 раза. Определить логарифмический декремент затухания колебаний
раза. Определить логарифмический декремент затухания колебаний 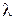 .
.
(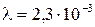 )
)
3. Тело, совершающее затухающие колебания, за время  с потеряло 60% своей энергии. Определить коэффициент затухания
с потеряло 60% своей энергии. Определить коэффициент затухания  .
.
(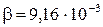
 )
)
4. Гиря массой 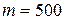 г подвешена к пружине жесткостью
г подвешена к пружине жесткостью 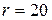 Н/м и совершает упругие колебания в некоторой среде. Логарифмический декремент затухания
Н/м и совершает упругие колебания в некоторой среде. Логарифмический декремент затухания  . Определить число полных колебаний
. Определить число полных колебаний  , которые должна совершить гиря, чтобы амплитуда колебаний уменьшилась в
, которые должна совершить гиря, чтобы амплитуда колебаний уменьшилась в 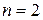 раза. За какое время
раза. За какое время 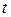 произойдет это уменьшение?
произойдет это уменьшение?
( t =172 с)
t =172 с)
5. Определить период 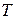 затухающих колебаний
затухающих колебаний 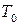 , если период собственных колебаний системы равен 1с, а логарифмический декремент затухания
, если период собственных колебаний системы равен 1с, а логарифмический декремент затухания 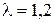 .
.
 с)
с)
6.* Математический маятник длиной 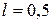 м, выведенный из положения равновесия, отклонился при первом колебании на
м, выведенный из положения равновесия, отклонился при первом колебании на  см, а при втором (в ту же сторону) на
см, а при втором (в ту же сторону) на 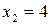 см. Найти время релаксации, т.е. время, в течение которого амплитуда уменьшится в
см. Найти время релаксации, т.е. время, в течение которого амплитуда уменьшится в 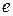 раз, где
раз, где 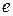 – основание натуральных логарифмов.
– основание натуральных логарифмов.
|
|
|
 с)
с)
7.* Колебательный контур состоит из конденсатора емкостью 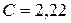 нФ и катушки длиной l =20 см из медной проволоки диаметром
нФ и катушки длиной l =20 см из медной проволоки диаметром  мм. Найти логарифмический декремент затухания
мм. Найти логарифмический декремент затухания 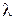 . Удельное сопротивление меди
. Удельное сопротивление меди 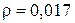 мкОм×м.
мкОм×м.
( )
)
8. Логарифмический декремент затухания колебаний в контуре 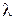 равен
равен  . Определить число полных колебаний
. Определить число полных колебаний  за которое амплитуда заряда на обкладках конденсатора уменьшилась в 2 раза.
за которое амплитуда заряда на обкладках конденсатора уменьшилась в 2 раза.
( )
)
9. Колебательный контур состоит из конденсатора емкостью  мкФ и катушки с индуктивностью
мкФ и катушки с индуктивностью 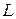 . За время
. За время  мс разность потенциалов на обкладках конденсатора уменьшается в четыре раза. Логарифмический декремент затухания
мс разность потенциалов на обкладках конденсатора уменьшается в четыре раза. Логарифмический декремент затухания 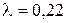 . Чему равны индуктивность
. Чему равны индуктивность 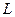 и сопротивление
и сопротивление  контура?
контура?
( мГн;
мГн; Ом)
Ом)
10. Колебательный контур имеет емкость 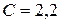 нФ и индуктивность
нФ и индуктивность  мГн. Логарифмический декремент затухания
мГн. Логарифмический декремент затухания 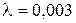 . Какой частью первоначального запасенной энергии будет обладать контур через время
. Какой частью первоначального запасенной энергии будет обладать контур через время  после начала колебаний (
после начала колебаний (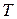 - период затухающих колебаний)? Чему равен коэффициент затухания
- период затухающих колебаний)? Чему равен коэффициент затухания ?
?
(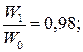
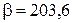
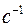 )
)
11. Определите логарифмический декремент затухания  , при котором энергия колебательного контура за
, при котором энергия колебательного контура за 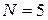 полных колебаний уменьшается в
полных колебаний уменьшается в  раз.
раз.
( )
)
12. Колебательный контур состоит из катушки индуктивностью  мГн, конденсатора емкостью
мГн, конденсатора емкостью  и резистора сопротивлением
и резистора сопротивлением  Ом. Определите, через сколько полных колебаний N амплитуда колебаний в контуре уменьшается в
Ом. Определите, через сколько полных колебаний N амплитуда колебаний в контуре уменьшается в 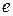 раз.
раз.
13. Гиря массой  кг, подвешенная на пружине жесткостью
кг, подвешенная на пружине жесткостью 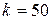 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления
Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления  кг/с. На верхний конец пружина действует вынуждающая сила, изменяющаяся по закону
кг/с. На верхний конец пружина действует вынуждающая сила, изменяющаяся по закону 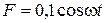 ,Н. Определите для данной колебательной системы: 1) коэффициент затухания
,Н. Определите для данной колебательной системы: 1) коэффициент затухания  ; 2) резонансную амплитуду A рез.
; 2) резонансную амплитуду A рез.
(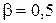
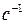 ; A рез=2 см)
; A рез=2 см)
14. Гиря массой  г, подвешенная на пружине жесткостью
г, подвешенная на пружине жесткостью 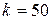 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления
Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления 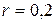 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону
кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону 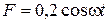 ,Н. Определите: 1) частоту собственных колебаний
,Н. Определите: 1) частоту собственных колебаний  ; 2) резонансную частоту nрез; 3) резонансную амплитуду
; 2) резонансную частоту nрез; 3) резонансную амплитуду 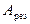 .
.
( Гц; nрез=7,88 Гц; A рез=2 см)
Гц; nрез=7,88 Гц; A рез=2 см)
15. Собственная частота  колебаний некоторой системы составляет 500 Гц. Определите частоту
колебаний некоторой системы составляет 500 Гц. Определите частоту  затухающих колебаний этой системы, если резонансная частота
затухающих колебаний этой системы, если резонансная частота 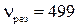 Гц.
Гц.
(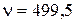 Гц)
Гц)
16. В цепь колебательного контура, содержащего последовательно соединенные резистор сопротивлением 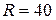 Ом, катушку индуктивностью
Ом, катушку индуктивностью 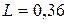 Гн и конденсатор емкостью C =28мкФ, подключено внешнее переменное напряжение с амплитудным значением Im =180В и частотой ω=314 рад/с. Определите: 1) амплитудное значение силы тока Im в цепи; 2) сдвиг по фазе между током и внешним напряжением.
Гн и конденсатор емкостью C =28мкФ, подключено внешнее переменное напряжение с амплитудным значением Im =180В и частотой ω=314 рад/с. Определите: 1) амплитудное значение силы тока Im в цепи; 2) сдвиг по фазе между током и внешним напряжением.
(Im =4,5А, φ = -1º, ток опережает напряжение)
17.* Катушка длиной l = 50 см и площадью поперечного сечения S = 10 см2 включена в цепь переменного тока частотой ν = 50 Гц. Число витков катушки N = 3000. Найти сопротивление катушки, если сдвиг фаз между напряжением и током φ = 60º.
(R = 8,36 кОм)
18. Обмотка катушки состоит из N = 500 витков медной проволоки (удельное сопротивление меди ρ = 0,017 мкОм·м), площадь поперечного сечения которой S = 0,5 мм2. Длина катушки l = 50 см, ее диаметр D = 5 см. При какой частоте переменного тока полное сопротивление Z катушки вдвое больше ее активного сопротивления R?
(ν = 59,6 Гц)
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 8580; Нарушение авторских прав?; Мы поможем в написании вашей работы!