Линейные комбинации строк и столбцов. Базисные строки и столбцы. Линейная независимость. Ранг матрицы. Вычисление ранга

Лекция 12

Свойство 5. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель, то величина определителя не изменится.

Свойство 6. Определитель треугольной матрицы равен произведению диагональных элементов.

=.

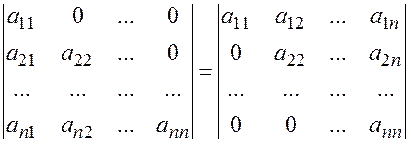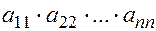нижний треугольный верхний треугольный

определитель определитель

Определение. Минором 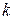-ого порядка матрицы называется детерминант матрицы порядка 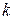, образованный элементами, стоящими на пересечении выбранных 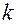строк и столбцов. Каждая матрица имеет столько миноров данного порядка, сколькими способами можно выбрать номера строк и столбцов. Если матрица квадратная, то каждому минору 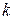– огопорядка сопоставляется дополнительный минор, который по определению есть определитель матрицы порядка (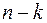), составленный из элементов, оставшихся после вычеркивания 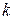строк и столбцов.

Цель: изучить понятие линейной комбинации и линейной независимости строк и столбцов матрицы, методы вычисления ранга и определения базисного минора.

В теме «матрицы и действия над ними» мы ввели понятия матрицы строки и матрицы столбца,

Определение. Столбец 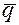назовем линейной комбинацией столбцов 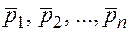одинаковой высоты, если при некоторых числах 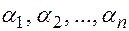имеет место равенство:

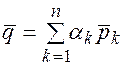(12.1)

Или в развернутом виде:

.

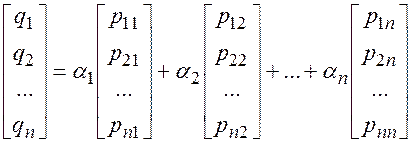В силу определения умножения матриц на число и операции сложения последнее равенство можно представить в виде системы равенств, составленных для каждого элемента:

;

;

…

.

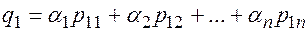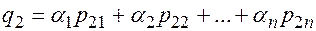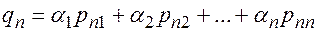По аналогии с линейной комбинацией введем понятие линейной независимости строк и столбцов матрицы. Пусть 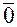- столбец у которого все элементы равны нулю.

Определение. Система из 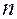столбцов 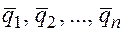называется линейно независимой, если из равенства 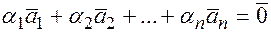следует, 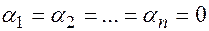. В противном случае, если не все 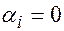(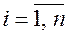), система столбцов линейно зависима.

Все утверждения записанные для столбцов, справедливы и для строк матрицы.

Пример: Столбцы

, ,

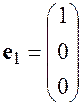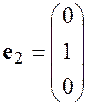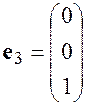
линейно независимы, т.к. их линейная комбинация

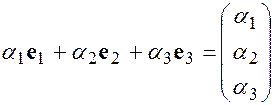
равна нулевому столбцу, только в случае, когда 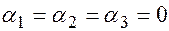, т.е. является тривиальной.

Дата добавления: 2013-12-11