Методы решения СЛАУ

Основные понятия и определения

Раздел 2. Решение систем линейных алгебраических уравнений

Некоторые обобщенные требования к выбору численных методов

Рассмотренные выше вопросы о погрешностях являются одними из важнейших моментов при выборе численного метода. В основе выбора численного метода лежат следующие соображения.

1) Можно утверждать, что нет ни одного метода, пригодного для решения всех задач одного и того же класса. Поэтому всегда стоит задача выбора численного метода (ЧМ), сообразуясь из конкретной технической задачи.

2) Численный метод можно считать удачно выбранным:

– если его погрешность в несколько раз меньше неустранимой погрешности, а погрешность округлений в несколько раз меньше погрешности метода;

– если неустранимая погрешность отсутствует, то погрешность метода должна быть несколько меньше заданной точности;

– завышенное снижение погрешности численного метода приводит не к повышению точности результатов, а к необоснованному увеличению объема вычислений.

3) Предпочтение отдается методу, который:

– реализуется с помощью меньшего числа действий;

– требует меньшего объема памяти ЭВМ;

– логически является более простым.

Перечисленные условия обычно противоречат друг другу, поэтому часто при выборе численного метода приходится соблюдать компромисс между ними.

4) Численный метод должен обладать устойчивостью и сходимостью.

5) По возможности нужно прибегать к существующему программному обеспечению ЭВМ для решения типовых задач.

6) Нужно помнить всегда, что ЭВМ многократно увеличивает некомпетентность Исполнителя технической задачи.

Системы линейных алгебраических уравнений (СЛАУ) являются важной математической моделью линейной алгебры. На их базе ставятся такие практические математические задачи, как:

– непосредственное решение линейных систем;

– вычисление определителей матриц;

– вычисление элементов обратных матриц;

– определение собственных значений и собственных векторов матриц.

Решение линейных систем является одной из самых распространенных задач вычислительной математики. К их решению сводятся многочисленные практические задачи нелинейного характера, решения дифференциальных уравнений и др.

Вторая и третья задачи являются также и компонентами технологии решения самих линейных систем.

Обычно СЛАУ n -го порядка записывается в виде

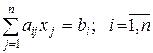
или в развернутой форме

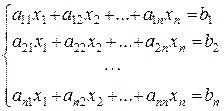(1)

или в векторной форме

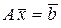, (2)

где

; ; .

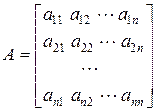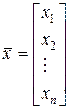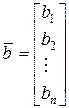В соотношениях (2):

А называется основной матрицей системы с n ² элементами;

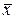= (x ₁, x ₂,..., x_n)^Т – вектор-столбец неизвестных;

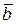= (b ₁, b ₂,..., b_n)^Т – вектор-столбец свободных членов.

Определителем (детерминантом – det) матрицы А n -го порядка называется число D (det A), равное

.

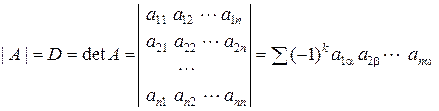Здесь индексы a, b,..., w пробегают все возможные n! перестановок номеров 1, 2,..., n; k – число инверсий в данной перестановке.

Первоначальным при решении СЛАУ (1) является анализ вида исходной матрицы А и вектора-столбца свободных членов 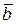в (2).

Если все свободные члены равны нулю, т.е. 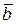= 0, то система 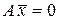называется однородной. Если же 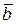¹ 0, или хотя бы одно b_i ¹ 0 (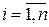), то система (2) называется неоднородной.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель | A | ¹ 0. При этом система (1) имеет единственное решение.

При | A | = 0 матрица А называется вырожденной, или особенной, а система (1) не имеет решения, либо имеет бесконечное множество решений.

Если | A |» 0 система (1) называется плохо обусловленной, т.е. решение очень чувствительно к изменению коэффициентов системы.

В ряде случаев получаются системы уравнений с матрицами специальных видов: диагональные, трехдиагональные (частный случай ленточных), симметричные (а_ij = a_ji), единичные (частный случай диагональной), треугольные и др.

Решение системы (2) заключается в отыскании вектора-столбца 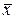= (x ₁, x ₂,..., x_n)^Т, который обращает каждое уравнение системы в тождество.

Существуют две величины, характеризующие степень отклонения полученного решения от точного, которые появляются в связи с округлением и ограниченностью разрядной сетки ЭВМ, – погрешность e и «невязка» r:

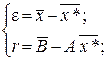(3)

где 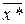– вектор решения. Как правило, значения вектора 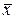– неизвестны.

Доказано, что если e» 0, то и r = 0. Обратное утверждение не всегда верно. Однако если система не плохо обусловлена, для оценки точности решения используют невязку r.

Методы решения СЛАУ делятся на две группы:

– прямые (точные) методы;

– итерационные (приближенные) методы.

К прямым методам относятся такие методы, которые, в предположении, что вычисления ведутся без округлений, позволяют получить точные значения неизвестных. Они просты, универсальны и используются для широкого класса систем. Однако они не применимы к системам больших порядков (n < 200) и к плохо обусловленным системам из-за возникновения больших погрешностей. К ним можно отнести: правило Крамера, методы обратных матриц, Гаусса, прогонки, квадратного корня и др.

К приближенным относятся методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы лишь с заданной точностью. Это итерационные методы, т.е. методы последовательных приближений. К ним относятся методы простой итерации, Зейделя.

Дата добавления: 2013-12-11