Волновое уравнение. Аналогично основному уравнению динамики, которое описывает все возможные движения материальной точки

Аналогично основному уравнению динамики, которое описывает все возможные движения материальной точки, в области волновых процессов также существуют уравнения, описывающие все волны, независимо от их конкретного вида. Это дифференциальные уравнения в частных производных, связывающие изменения функции характеризующей волну, в пространстве и во времени.

Найдем эту связь для одномерных плоских волн типа 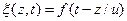. Введем величину фазы волны 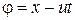. Тогда

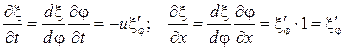
Сопоставив полученные выражения, получаем

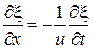(27.12)

Это уравнение справедливо для волн, распространяющихся в положительном направлении оси 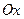. Для волн, распространяющихся в противоположном направлении

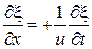(27.13)

Таким образом, для обоих случаев распространения уравнение принимает вид

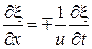(27.14)

Знаки «-» и «+» относятся к волнам, бегущим, соответственно, в положительном и отрицательном направлении оси .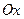

Полученное уравнение является простейшим волновым уравнением. Во многих случаях оно является чрезвычайно полезным.

Поясним физический смысл производных, входящих в волновое уравнение. Производная по времени

(27.15)

- это проекция скорости частицы среды, движущейся около своего положения равновесия; а производная

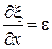(27.16)

относительная деформация среды. Поясним этот термин.

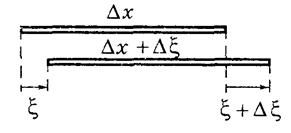Выделим мысленно малый (по сравнению с изменением профиля волны) цилиндрический элемент среды 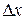вдоль направления распространения волны. Поскольку колебания торцов выделенного элемента происходит со сдвигом по фазе, то в каждый момент времени они сдвинуты относительно положения равновесия не разные расстояния. Следовательно, при прохождении продольной волны этот элемент будет смещаться и деформироваться. Пусть левый конец отклонился от равновесного положения на величину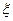, а правый – на величину . По определению относительная деформация определяется выражением

(27.17)

Относительная деформация – алгебраическая величина: она может быть положительной (растяжение) и отрицательной (сжатие).

Согласно уравнению (14), в данной точке среды в данный момент времени относительная деформация пропорциональна скорости смещения относительно равновесного положения:

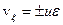(27.18)

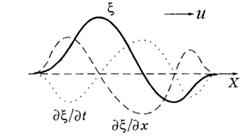Пример. Продольная волна распространяется в длинном стержне (ось 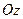). В некоторый момент смещения частиц из положения равновесия имеют вид 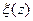как на рисунке. Зная, что волна распространяется в положительном направлении оси 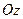, найдем (качественно) зависимость скорости частиц среды от координаты 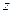в этот же момент времени.

Согласно волновому уравнению (14), пространственная и временная производные возмущения связаны линейной зависимостью. При этом пространственная производная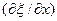в каждой точку характеризует наклон (крутизну) криво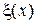й к оси 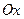. Изобразим график 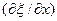как функцию 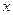штриховой линией. Поскольку волна распространяется в положительном направлении оси 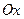, знак в волновом уравнении должен быть отрицательным. Это значит, что график 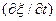как функции 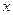является зеркальным отражением графика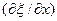. Он изображен точечной кривой.

Общее волновое уравнение. Получим уравнение справедливое для волн, распространяющихся в любом направлении, а также для суперпозиции таких волн. Дифференцируя возмущения вида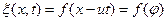, получаем

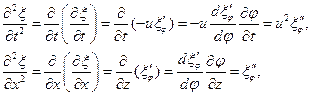
Отсюда следует

(27.19)

Это одномерное волновое уравнение второго порядка. Ему удовлетворяют все возмущения вида

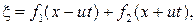
где 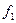,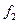- произвольные функции. Данное уравнение справедливо для сред, затухание в которых пренебрежимо мало.

Волновое уравнение для трехмерных волн

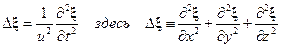- оператор Лапласа. (27.20)

Волновое уравнение играет важную роль в теории волновых процессов. Если мы, исходя из законов механики при изучении некоторого явления, придем к любой форме этого уравнения, то сразу можем утверждать о его волновом характере.

Уравнение (20), в отличие от уравнения (19), описывает не только плоские волны, но и волны с произвольной формой поверхности постоянной фазы, в частности, сферические и цилиндрические волны.

Сферическая волны. В однородной изотропной среде продольная волна от точечного источника представляет собой сферически расходящееся возмущение вида

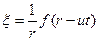(27.21)

где 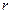– расстояние от точечного источника возмущения. В частности, если источник возбуждает продольные монохроматические колебания, то уравнение (21) принимает вид

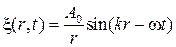(27.22)

где - постоянная, 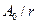– амплитуда волны. В присутствие линейного поглощения

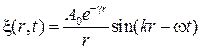(27.23)

Цилиндрическая волна. Такие волны распространяется от источников, равномерно распределенных вдоль оси в однородной среде. Структура цилиндрической волны значительно сложнее сферической. Ее форма (в отличие от плоской или сферической волн) не повторяет временного поведения функции источника: волна тянет за собой длинный «шлейф». И только на больших расстояниях 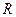от источника ее можно представить виде

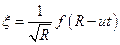
В частности, монохроматическая расходящаяся волна на расстояниях 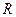, значительно превышающих длину волны, имеет вид

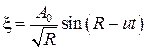
Дата добавления: 2013-12-13