Учет начисленных сумм платежей

Список использованной литературы

1. Карташев А. П., Рождественский Б. Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. – М.: Наука, 1979-288 с.

2. Краснов М. Л. и др. Сборник задач по обыкновенным дифференциальным уравнениям: Учеб. пособие для вузов. – М.: Высш. шк., 1989-383 с.: ил.

3. Самойленко А. М., Кривошея С. А., Перестюк Н. А. Дифференциальные уравнения: примеры и задачи: Учеб. пособие. – М.: Высш. шк., 1989-383 с.: ил.

1.Описание движения в пространстве состояний. Математические модели процессов и систем

Метрика пространства состояний начинает фигурировать па стадии решения конкретных задач устойчивости, управляемости, оптимизации. Поэтому при записи уравнений в пространстве состояний можно указывать лишь размерность пространства, полагая на этом первом этапе метрику, например, евклидовой, или вообще не задавать метрики.

1.1.Детерминированная управляемая система, описываемая векторным дифференциальным уравнением в форме Коши.

Если возмущающие воздействия являются детерминированными (регулярными, неслучайными), то их можно представить в виде известных функций времени и уравнение указанной системы записать в виде

ẋ = f(x, u, t), (1)

где х€ Rⁿ , u€ R^r, а точкой отмечена полная производная вектора х по времени t. Что касается векторной функции f векторных аргументов x, u и скалярного аргумента t, то она считается заданной и принадлежащей некоторому классу функций, допускающему существование решения уравнения (1) (при заданных x(t₀), u(t) или и(х, t)) во всем пространстве состояний, либо в его областях, охватывающих интересующую исследователя часть пространства состояний. В более сложном и общем случае рассматриваемая область пространства состояний разделена на подобласти, для каждой из которых задана своя непрерывная функция f, удовлетворяющая указанному условию в области определения. Поведение системы на границах подобластей доопределяется, т. е. определяется дополнительными условиями (например условиями непрерывности).

Наряду с понятием «система» или «динамическая система» будем использовать понятие процесса. Если система описывается уравнением (1), то процесс в этой системе описывается решением уравнения (1) при определенном печальном условии x(t₀) = х₀ и определенном управлении, например u = u(t). Вместо одного процесса может рассматриваться множество процессов, соответствующее некоторому заданному множеству начальных условий и заданному множеству управлений. Для отличия описания системы и процесса вектор состояния процесса иногда будет обозначаться x_t.

Процессы в непрерывном пространстве состояний Rⁿ, описываемые уравнением вида (1) и другими указанными ниже обыкновенными дифференциальными уравнениями, для краткости называются непрерывными процессами. При обычных условиях существования решения дифференциальных уравнений процесс х(t)-действительно непрерывная функция времени. При расширенных условиях существования, когда f содержит так называемые δ-функции или состоит из нескольких непрерывных функций, определенных в подобластях пространства состояний, сшиваемых без условия непрерывности решения, возможны разрывы непрерывности x(t). Эти случаи, как правило, оговариваются особо, и соответствующим системам придаются подходящие наименования.

1.2.Детерминированная непрерывная система с линейно входящими управлениями.

Широкий класс систем допускает при описании пользоваться линейным по вектору управления и уравнением вида

ẋ = f(x, t) + φ(х, t)u, (2)

где х€ Rⁿ , u€ R^r, f(x, t) - векторная функция векторного х и скалярного t аргументов, φ(x, t)-матричная функция размера nXr аргументов х, t.

1.3.Детерминированная линейная непрерывная управляемая система.

Рассматривается система, изменение состоянии которой во времени описывается уравнением

ẋ = A(t)x + D(t)u (3)

ẋ = Ах + Вu, (4)

где х€ Rⁿ , u€ R^r, А - матрица коэффициентов (в общем случае функций времени) размера nХn; В - матрица коэффициентов (в нестационарном случае также функций времени) размера nXr. Если А и В являются матричными функциями времени (как в (3)), то линейная система называется нестационарной. Если А = const, В = const, то линейная система стационарна.

Общее решение уравнения (3) может быть записано в виде

х (t) = K (t, t₀) х (t₀) + ∫ K (t, θ) B (θ) u (θ) dθ,

где K(t, tꞌ) - матрица Коши системы (3), удовлетворяющая матричному уравнению и начальному условию

d/dt K(t, tꞌ) = A (t) K(t, tꞌ), K(t, tꞌ) = E,

где Е - единичная матрица. Матрица Коши является частным видом фундаментальной матрицы системы (3), которой называют любую невырожденную матрицу W(t, tꞌ), удовлетворяющую d/dt W(t,tꞌ) = A(t)W (t, tꞌ)

При анализе систем вида (3) широко используется матрица Ф (t, tꞌ) = K(t, tꞌ) B(tꞌ), называемая импульсной переходной матрицей или весовой матрицей. Столбцы этой матрицы можно рассматривать как реакцию системы (3) на входные воздействия в виде δ-имнульсов, подаваемых на каждый из входов (компоненты вектора u) при пулевых начальных условиях.

Сравнительно реже используется переходная матрица, определяемая соотношением

H (t, tꞌ) = ∫ Ф (t, θ) dθ,

столбцы которой являются реакцией системы на единичные входные воздействия, подаваемые па каждый из входов, при нулевых начальных условиях.

У стационарных систем матрица Коши, весовая и переходная матрицы являются функциями только относительного времени t᷃ = t - tꞌ.

1.4.Стохастическая управляемая система, описываемая уравнением в форме Ито.

Для описания движения динамической стохастической системы используется уравнение

dx = f(x, u, t)dt + g(x, t)dw(t), (5)

где х€ Rⁿ , u€ R^r, f- векторная функция указанных аргументов, w(t)- q-мерный винеровский случайный процесс, g(x, t)-матричная функция размера n × q

Уравнение Ито в дифференциальной форме (5) является символическим и означает, что случайный процесс x(t) = x_t удовлетворяет равенству

х (t₂) - х (t₁) = ∫ f [x(τ), u (τ), τ] dx + ∫g [х (τ), τ] dw (τ)

при всех t₁ < t₂ из промежутка «функционирования системы» (5). Второй интеграл в правой части последнего выражения- стохастический интеграл Ито. Он может быть приближен в среднем квадратическом интегральными суммами, такими же, как и обычный интеграл Римана - Стилтьeса.

1.5. Стохастическая управляемая система, описываемая уравнением в форме Ланжевена.

Другая форма описания динамической системы сводится к уравнению

ẋ =f (x,u,t) + g(x,t) ξ(t), (6)

где ξ(t) - q-мeрный случайный процесс типа белого шума с нулевым математическим ожиданием E[ξ(t)] = 0 и ковариационной матрицей вида

E [ξ(t) ξ^T (tꞌ) ] = ψ (t) δ (t - tꞌ),

Ψ(t) - матричная функция времени размера q×q. Конкретную реализацию случайного процесса x(t), удовлетворяющего (6), будем обозначать x_t.

Процесс в виде белого шума доставляет много неприятностей математику. Действительно, при любой модели белый шум имеет бесконечные дисперсии своих компонент и разрывный характер при любом текущем значении t. При этом использование моделей белого шума, получаемых путем предельных переходов в некоторых исходных искусственных моделях, может давать различные результаты в предельных формах решений обыкновенных дифференциальных уравнений. Поэтому в строгой трактовке уравнения типа (5), (6) есть просто условные обозначения соответствующих интегральных уравнений, в которых интегралы имеют неклассический обобщенный смысл (интеграл Ито, интеграл Стратоновича). Однако для инженера и физика совсем не обязательна такая строгая трактовка стохастических уравнений с белым шумом. Дело в том, что вместо белого шума, которого в природе не существует, можно рассматривать широкополосный шум (с интервалом корреляции, намного меньшим всех характерных постоянных времени рассматриваемой динамической системы). Каждая реализация такого широкополосного шума может удовлетворять условиям существования и единственности уравнения (6), рассматриваемого как обыкновенное дифференциальное уравнение. Такой широкополосный шум (с ограниченными дисперсиями) будем называть практически белым шумом. Подобное название оправдано следующим. Па практике преимущественно применяются те математические модели динамических систем, которые обладают грубостью не только по отношению к собственным параметрам, но и по отношению к форме возмущающих воздействий. Для таких моделей воздействие белого шума и практически белого шума в достаточной степени одинаково. Поэтому пет необходимости прибегать к сложным и трудно усваиваемым инженерами математическим конструкциям и понятиям тина интегралов Ито и Стратоновича.

1.6. Стохастическая управляемая система, описываемая уравнением в форме Ланжевена с аддитивным белым шумом.

Частным случаем (6) является случай, когда справедливо уравнение

ẋ= f(x,u,t) + ξ(t), (7)

где ξ(t) - q-мерный случайный процесс типа белого шума:

Е[ξ(t)]=0, E[ξ(t) ξ^T(tꞌ)] = Q(t) δ (t - tꞌ), (8)

Q(t)-матричная функция времени размера q×q, называемая матрицей интенсивностей или (в случае Q = const) матрицей спектральных плотностей белого шума.

1.7. Линейная стохастическая управляемая система в форме Ланжевена.

Уравнение (6) в частных случаях может быть представлено в виде

ẋ = A (t)x + B(t)u + C(t) ξ(t), (9)

где ξ(t) - q-мерный случайный процесс типа белого шума, C(t)-матрица коэффициентов размера n×q.

1.8.Уравнение Фоккера - Планка - Колмогорова (ФПК-уравнение) для безусловной плотности вероятности в пространстве состояний непрерывной стохастической системы.

Стохастические непрерывные динамические системы, помимо обыкновенных дифференциальных стохастических уравнений в форме Ито или в форме Ланжевена, имеют принципиально отличную форму описания в виде уравнений в частных, производных для плотности вероятности. Если уравнения вида (5) - (9) описывают каждую реализацию случайного процесса, то нижеследующие уравнения в частных производных описывают эволюцию статистической характеристики - плотности вероятности нахождения изображающей точки в евклидовом пространство состояний. Естественно, что начальная плотность вероятности р(х, t₀) считается заданной. Могут задаваться разнообразные граничные условия. Тогда для случая (6), где f, g и ψ считаются дифференцируемыми, при фиксированном и текущая плотность вероятности р = р(х, t) подчиняется ФПК-уравнению вида

(10)

Здесь (gψg^T)_ij, - элемент матрицы gψg^T размера n×n. Если начальное распределение удовлетворяет условию нормировки, то решение (10) автоматически удовлетворяет этому условию:

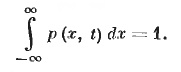(11)

Здесь интегрирование ведется по всему пространству Rⁿ. Для случая (7), (8) при фиксированном и ФПК-уравнение (10) принимает вид

(12)

Если вместо обычной плотности вероятности р использовать логарифмическую плотность вероятности ln р, то ФПК-уравнение (12) преобразуется к виду

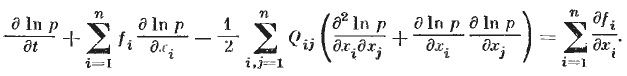(13)

1.9.Уравнение Стратоновича для апостериорной плотности вероятности в пространстве состояний наблюдаемой стохастической системы.

Введем вектор наблюдения (измерения) для процесса, например, вида (6):

z = h(x_t,t) +η(t) (14)

Здесь h(x_t,t)-заданная векторная функция (размера m×1) указанных аргументов, η(t) - гауссов случайный процесс тина белого шума с корреляционной матрицей

E [η(t) η^T (tꞌ)] = R(t) δ(t - tꞌ) (15)

где R(t) -матрица н интенсивностей; x_t -решение уравнения (6), т. е. истинное состояние наблюдаемого процесса. Для устранения трудностей понимания, связанных с бесконечной дисперсией процесса η(t), вместо белого шума можно рассматривать практически белый шум.

Пусть стохастический процесс x(t) = x_t наблюдается в соответствии с (14) на замкнутом интервале времени от t₀ до t. Совокупность полученных в результате наблюдения па этом интервале значений функции z(t) обозначим через Z. Ясно, что апостериорная или условная плотность вероятности в пространство состояний р(х, t Z), полученная после наблюдения z(t), будет отличаться от безусловной или априорной плотности вероятности р(х, t), определяемой ФПК-уравнением. Эта апостериорная плотность вероятности определяется уравнением Стратоповича, которое для случая (6), (14) при использовании обозначения р = р(х, t I Z) имеет вид [1.5]

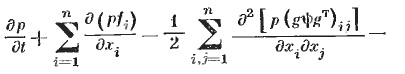
(16)

(17)

- оценка функции наблюдения, являющаяся условным математическим ожиданием h(х, t). Через х* в (17) обозначена переменная интегрирования по пространству состояний. Если х - истинный вектор состояния, то функция р(х*, t I Z) должна зависеть от х, имея, в частности, экстремум при х* = х. Поэтому в (17) указана зависимость h от х.

1.10. Детерминированная управляемая нелинейная система с дискретным временем.

Системы с дискретным временем описываются разностными уравнениями. Для непрерывных нелинейных систем, описываемых уравнениями типа (1), как и для других нелинейных систем с непрерывным описанием, в подавляющем большинстве случаев могут быть получены лишь приближенные разностные модели (разностные схемы). Исключение составляет случай, когда на каждом интервале дискретизации при известном законе изменения и па данном интервале (па-пример, при постоянстве и в пределах интервала) уравнение (1) интегрируется в общем виде. Действительно, общее решение задачи Коши для (1) при x(tk) = х[k], u(lk) = u[k] = u(t), если tk ≤ t < t_k+1, имеет вид x[k + 1] = F(x[k], u[k], k).

Если общее решение (1) неизвестно, то может быть построено разностное уравнение (разностная схема), приближенно эквивалентное (1), т. е. приближенно выражающее зависимость x(t_k+1) от значений х, u, t в предшествующий момент времени t_k и, вообще говоря, t _k-1,t _k-2,… (для так называемых многошаговых методов). Различные раз-иостпые схемы уравнения типа (1) и других дифференциальных уравнений рассматриваются в обширной литературе по численному интегрированию обыкновенных дифференциальных уравнений. Разностная схема Эйлера имеет вид

x[k + l]. = x[k] + τ f(x[k], u[k], k),

где τ = t_k+1 – t_k - шаг дискретизации. Правая часть в разностном уравнении часто будет обозначаться, как и в обыкновенном дифференциальном уравнении, через f, и детерминированная нелинейная управляемая система с дискретным временем будет представляться в виде

х[k + 1] = f(x[k], u[k], k). (18)

1.11.Стохастическая нелинейная управляемая система с дискретным временем.

Обобщение уравнения (18) получается за счет учета случайных возмущающих воздействий в виде случайной последовательности w [k], в частности, некоррелированной центрированной гауссовской случайной последовательности: E[w[k]] =0, E[w[k]w[k -l ]^т] =0, l= 1, 2, 3,…(дискретный белый шум), а также, быть может, учета вектора параметров а, которые считаются постоянными или медленно меняющимися величинами.

Соответствующее разностное уравнение имеет вид

x[k + 1] = f(x[k], u[k], a[k], w[k], k). (19)

1.12. Детерминированная линейная управляемая система с дискретным временем.

Указанная система описывается следующим линейным разностным уравнением:

x[k+1]. = A[k]х[k] + В[k]u[k]. (20)

Линейные непрерывные системы вида (3) относятся к тому классу систем, для которых известно общее решение

х (t) = К (t, t₀) х (t ₀) + ∫ К (t, τ) В (τ) и (τ) dτ, (21)

где К (t, t₀) -матрица Коши (фундаментальная матрица) непрерывной системы, удовлетворяющая уравнению

d/dt *K(t, t₀) = A(t) К(t, t₀) (22)

при условии

К(t₀, t₀) =Е, (23)

где Е - единичная матрица.

При постоянстве управления u(t) = u [k] на каждом интервале от t_k до t_k+1 и ступенчатом его изменении в указанные моменты времени из (21) следует (20), где

(24)

Обозначения В [k] и B(τ) здесь соответствуют разным функциям.

Матрица Коши дискретной во времени системы (20) К [k, j] однозначно определяется уравнением (k > j)

К [k + 1, j] = А [k] K[k, j] (25)

и условием

К[j, j] = Е. (26)

Из (25), (26) следует при k > j;

К [k, j] = А [k - 1] А [k - 2]... А [j]. (27)

Решение разностного линейного уравнения (20) имеет вид

(28)

1.13.Стохастическая лилейная управляемая система с дискретным временем.

Эта система отличается от системы (20) только наличием аддитивного случайного члена:

х[k + 1] = А [k] х[k] + В[k] u[k] + w[k]. (29)

Случайная последовательность w[k], k = 1, 2,..., в частности, может быть белой гауссовской. Тогда E[w[k]] =0, E[w [k]w^T[k- l]] = 0, l = 1, 2,... Процесс x [k] (29) при заданном и в этом случае является марковским дискретным во времени процессом.

2. Наблюдаемость

Измерение, наблюдение является необходимей составной частью управления. Даже тогда когда формируется так называемое программное управление - функция времени, определяемая, например, на стации проектирования, исходным является измерение, доставившее необходимую информацию об управляемом процессе. Связь управления с информацией, получаемой посредством измерении, является органической и может быть положена в основу определении понятия управления.

При автоматическом управлении предполагается, что наблюдение) сопровождается измерением координат, параметров, и в понятия наблюдение, измерение вкладывается практически одинаковый смысл. В дальнейшем в основном будет применяться термин наблюдение. В отличие от тождественности понятий наблюдение и измерение, понятия наблюдаемость и измеримость имеют, вообще говори, различное содержание в теории автоматического управления. Под измеримостью понимается возможность непосредственного измерения той или иной физической величины. Синонимом этого понятия является непосредственная наблюдаемость. Под наблюдаемостью (по крайней мере в узком смысл) понимается возможность косвенного определения величии на основе измерения некоторых других величии и использовании априорной информации (восстановления величин). Косвенные измерения широко известны из классической метрологии. В теории управления под наблюдаемостью понимается возможность косвенных измерений, но в расширенном по сравнению с традиционной метрологией смысле.

Можно рассматривать наблюдаемость как в пространстве состояний, так и в пространстве сигналов. Однако компоненты вектора сигналов чаще всего выбираются измеримыми, так что в пространстве сигналов обычно имеет место непосредственная наблюдаемость.

Завершая вводные положения, отметим, что можно применять обобщенное понятие наблюдаемости, включающее как непосредственную, так и косвенную наблюдаемость.

2.1. Виды общей наблюдаемости в пространстве состояний.

Достаточно общая постановка задачи определения состояния системы по наблюдениям заключается в следующем.

Получено (через наблюдение) множество Z, связанное известным оператором с множеством X, принадлежащим пространству состояний системы с заданной математической моделью. Требуется определить X или никоторое его подмножество Хи X.

В технической интерпретации это выглядит следующим образом. Известно множество выходных величин идеальных (без шумов, но в общем случае инерционных) измерителей заданных функций состояния контролируемого процесса, подчиняющегося точно известным уравнениям. Требуется определить множество (или подмножество) состояний процесса, которому соответствует указанное множество выходных величии.

Заметим следующее. Измерители, которые фигурируют в поставленной задаче, как правило, могут быть описаны обыкновенными дифференциальными или разностными уравнениями. Тогда путем расширения пространства состояния можно задачу с операторной связью между множествами состояний и наблюдений заменить задачей с функциональной связью между этими множествами и сформулировать ее так.

Получено (через наблюдение) множество Z, связанное заданной функцией Z(X) с множеством состояний X системы с известным уравнением. Требуется определить X или подмножество Хн X.

В зависимости от видов множеств Z, X, функции Z(X) и уравнений наблюдаемого процесса возможно, как уже отмечалось, большое число вариантов конкретных постановок задачи наблюдения. Пусть элемент множества X представляет собой текущее значение вектора состояния х, а элемент множества Z - векторную функцию от х той же размерности n, что и х: z = h(x), x€Rⁿ, z€Rⁿ. Этот вариант можно назвать случаем полнокомпонентного мгновенного измерения. Его иллюстрирует рис. 2.1.1, а. Изогнутая стрелка означает здесь преобразование вектора х в равноразмерный вектор z.

Задача сводится к общеизвестной задаче разрешимости системы n нелинейных (в общем случае) алгебраических уравнений относительно п неизвестных. Априорная информация в виде уравнений, определяющих x(t), здесь не используется. Этот случай для теории оценивания

Рис. 2.1.1. Иллюстрации постановок задачи наблюдения

малоинтересен, так как полнокомпонентное измерение в динамических системах встречается редко.

К случаю полнокомпонентного мгновенного измерения в некотором смысле примыкает случай однокомпонентного измерения на заданном (возможно, сколь угодно малом) интервале времени с возможностью вычисления n-1 производных по времени z, z … z ^(n-1) В этом случае элемент множества X задан в виде дифференцируемого необходимое число раз решения уравнения наблюдаемого детерминированного процесса на том же интервале времени [t, t + ∆t] (известно уравнение процесса, а не сам процесс х(t)). Элемент множества Z в данном случае представляет скалярную дифференцируемую n-1 раз функцию z(t) = h(x(t)), измеряемую па интервале [t, t + ∆t]. Этот случай иллюстрирует рис. 2.1.1, б. Его будем называть практически мгновенным скалярным наблюдением с вычислением производных. Он имеет невысокое практическое значение, так как при наличии шумов измерения вычисление указанных производных по времени сопряжено с известными трудностями.

Самая распространенная постановка задачи наблюдения такая, при которой элементом множества X является вектор состояния в некоторый начальный момент времени x(t0), известно уравнение детерминированного процесса, которому подчиняется x(t), задана функция наблюдения z - h[x(t), t], измеряемая на конечном интервале времени [t0, t1], t1 > t0, и имеющая размерность меньше размерности х. Таким образом, элементом множества Z здесь служит функция z(t) на указанном интервале, причем число компонент векторной функции z(t) заведомо меньше числа компонент х(t) ив частном случае z(t) = z1(t) может представлять скалярную функцию при многомерном пространстве состояний. Соответствующая иллюстрация приведена па рис. 2.1.1, в. Ясно, что задача определения (восстановления) x(to) в этой постановке разрешима только за счет использования априорной информации об x(t), т. е. уравнения процесса.

На практике решение последней задачи почти эквивалентно решению задачи восстановления текущего вектора состояния по измерениям текущего значения функции наблюдения. Действительно, за начальный момент времени в данной задаче можно выбрать любой момент, предшествующий конечному моменту наблюдения t1. Поэтому при соблюдении соответствующих условий может быть восстановлено состояние процесса, непосредственно предшествующее текущему и для непрерывных процессов мало отличающееся от текущего (рис. 2.1.1, г).

Во всех рассмотренных выше постановках задачи наблюдаемости множество А имеет такую же размерность, что и пространство состояний. Если возможно определение (восстановление) полного вектора состояния, то говорят о полной наблюдаемости. Соответствующая система называется вполне наблюдаемой. Если же существует возможность вое становления лишь подмножества Хн X, а именно части компонент вектора состояния, другая лее часть не может быть определена в заданных условиях, то имеет место неполная наблюдаемость, а система называется не вполне наблюдаемой.

Изучение наблюдаемости, как и других свойств систем, нуждается в критериях, условиях, которые позволяли бы судить о наблюдаемости на основе некоторых правил, оперирующих априорной информацией (заданными условиями). Эти критерии и составляют основное содержание теории наблюдаемости.

В заключение перечисления видов наблюдаемости укажем определение используемого иногда понятия степени непосредственной наблюдаемости или измеримости. При полной непосредственной наблюдаемости h(x) = х и z = х. При неполной непосредственной наблюдаемости h (х) = Нх, где - диагональная матрица, имеющая в блочном изображении вид

(1)

Здесь Ev - единичная матрица v X v, v < п (n- размерность x). Отношение v/n называется степенью непосредственной наблюдаемости или измеримости. Конечно, непосредственно измеряемые координаты могут иметь первоначально произвольные индексы из числа n индексов. Матрица непосредственного наблюдения приводится к виду (1) путем присвоения измеряемым компонентам вектора состояния первых индексов.

2.2. Локальное условие, благоприятствующее полной наблюдаемости для полнокомпонентного мгновенного измерения.

Как известно, нет общих условий однозначной разрешимости системы нелинейных урав-иепий

(2)

эквивалентных векторному уравнению z = h(x). Однако пеобходпмое и достаточпос локальное условие для гладкой функции h имеет вид

(3)

Здесь dh/dх - матрица Якоби, [dh/dx]-якобиан (определитель матрицы dh/dх). Если условие (3) выполнено в некоторой точке x° и z° = h(х°), то при z, близких к z°, уравнение z = h (х) имеет единственное решение х = F(z) в окрестности x°. Кроме того, в окрестности x° малым приращения ∆z соответствуют малые приращения ∆х, т. е. система наблюдения является «грубой» по отношению к ошибкам измерения. Геометрическая интерпретация условий (2), (3) широко известна.

Рис. 2.1.2. Геометрическая интерпретация локального условия при полнокомпонентном измерении

Если выражения (2) при заданных zt рассматривать как поверхности положения в пространстве состояний (навигационная терминология), то состояние определится как точка пересечения п таких поверхностей и из условий (3) следует единственность такой точки. Условие (3) означает, что в окрестности точки х все поверхности положения различны в том смысле, что нормали к ним не коллинеарны (рис. 2.1.2). Как уже отмечалось, свойственная данному случаю полнота наблюдения (n измеряемых величин, связанных с n-мерным вектором состояния) редко имеет место в системах со сложными (детальными) математическими моделями. Поэтому данный вариант в теории управления часто вообще не рассматривается.

2.3. Локальное условие полной наблюдаемости при вычислении (измерении) производных по времени.

Уравнение детерминированного процесса имеет вид

ẋ= f (x, u, t), (4)

где u= u(t)-известная дифференцируемая нужное число раз функция времени, х € Rⁿ. Уравнение наблюдения записывается в несколько более общей форме, чем ранее, т. е.

z= h(x, u, t), (5)

где z - векторная наблюдаемая величина размерности т. Заданные функции f и h считаются дифференцируемыми по всем аргументам необходимое число раз.

Введем линейный оператор дифференцирования в силу уравнения (4) (оператор Ляпунова)

(6)

где звездочкой обозначены функции-столбцы.

Дифференцируя (5) n- 1 раз но времени, получаем с учетом (6)

(7)

Соотношения (7) рассматриваем как уравнения относительно х при заданных (измеренных или вычисленных по z(t)) левых частях. Вследствие самого способа получения данных соотношений вектор состояния x(t) системы (4) является решением этих уравнений, причем именно тем решением, которое необходимо найти по смыслу задачи наблюдения. Для однозначного определения x(t) в этих условиях необходимо и достаточно, чтобы

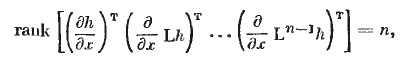(8)

где все матрицы Якоби вычислены па решении х = x(t) при известном управлении u(t).

2.4. Локальное условие неполной наблюдаемости.

Повторяя приведенные в п. 2.3 преобразования, убеждаемся, что если измеряется (вычисляется), как и выше, (n- 1)-я производная z, но

(9)

то имеет место неполная наблюдаемость в том смысле, что по результатам измерения (вычисления) производных могут быть определены d < n компонент вектора состояния. Степень наблюдаемости (не непосредственной, о которой говорилось в п. 2.1, а косвенной) естественно определить как отношение d/n.

Допустим, что h = х. Это означает, что имеет место полная измеримость или полная непосредственная наблюдаемость. В этом случае dh/dx = Е - единичная матрица размера n×n. Ранг матрицы в левой части выражения (8) равен и, и имеет место полная наблюдаемость. Полная наблюдаемость, очевидно, имеет место и при выполнении условия (3).

2.5. Структурная интерпретация наблюдаемости.

Разобьем вектор х па два субвектора х = (x₍₁₎, x₍₂₎) (это эквивалентно представлению матрицы-столбца в блочной форме). Уравнения (2.4), (2.5) запишутся в виде

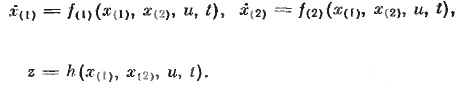(10)

Структурная схема, соответствующая этим уравнениям, в условных изображениях, (см. рис. 1.3.2, а), представлена па рис. 2.1.3.

Рис. 2.1.3. Структура процесса, который может быть как вполне наблюдаемым, так и не вполне наблюдаемым

Процесс, отвечающий этой структурной схеме, может быть как вполне наблюдаемым, так и не вполне наблюдаемым. Полная или неполная наблюдаемость в локальном смысле может быть установлена посредством критериев (8), (9). Допустим теперь, что уравнения имеют следующую форму:

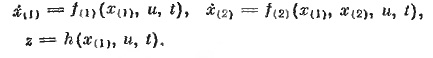(11)

Соответствующая структурная схема представлена па рис. 2.1.4. Непосредственно из этой структурной схемы видно, что процесс, характеризуемый вектором состояния x₍₂₎, понаблюдаем, так как x₍₂₎ никак не

Рис. 2.1.4. Структура не вполне наблюдаемого процесса

воздействует на выход системы z. Если размерность равна d, а размерность x₍₂₎ соответственно (n - d), то степень наблюдаемости здесь не более d/n. Это вытекает и из аналитического критерия (9). Действительно, матрица (dh/dx) имеет в данном случае следующую блочную структуру: (dh/dx) = [(dh/dx) 0], причем размер нулевой матрицы-блока (n - d) ×m. Все другие матрицы 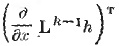имеют такую же блочную структуру (с нулевыми блоками того же размера). Ранг матрицы в левой части выражения (9) здесь не может превышать d.

2.6. Условие наблюдаемости линейной стационарной системы.

Для нелинейной системы следует говорить о наблюдаемости того или иного процесса (движения), происходящего в этой системе. Для линейной системы и линейных условий наблюдения все процессы имеют одинаковую степень наблюдаемости. Поэтому можно говорить просто о наблюдаемости линейной системы.

Условие наблюдаемости линейной стационарной системы было получено Калманом, который одновременно ввел наиболее распространенное понятие наблюдаемости (и управляемости).

Пусть уравнение процесса и уравнение наблюдения имеют вид

ẋ= Ах + Вu, z = Нх + Си,

где А, В, Н, С - постоянные матрицы.

Оператор (6) в данном случае принимает форму

Функция h здесь равна Нх + Си. Критерий (8) приобретает вид

(12)

Это широко известное необходимое и достаточное условие полной наблюдаемости Калмана. Матрица, обозначенная квадратными скобками, здесь состоит из матриц-блоков размера n × m и имеет общий размер n × m. Иногда эти блоки отделяют штриховыми линиями, записывая

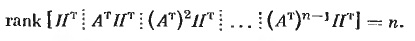
Для случая неполной наблюдаемости будем иметь

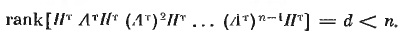(13)

Степень наблюдаемости в этом случае d/n.

Степень наблюдаемости не меняется при линейном неособом преобразовании координат. Действительно, если выполнить преобразование х - аy, где а - невырожденная квадратная матрица, то условие (13), примененное к системе с вектором состояния y, будет иметь вид

Ранг матрицы в левой части этого выражения такой же. как ранг матрицы в левой части (13). Можно показать, что если наблюдаемость линейной стационарной системы не полная, то она или непосредственно имеет структуру, показанную на рис. 2.1.4, или может быть приведена к этой структуре линейным неособым преобразованием пространства состояний.

2.7. Условие наблюдаемости линейной нестационарной системы.

Уравнения процесса и наблюдения имеют вид

ẋ = А (t)х + B(t)u, z = H(t)x + C(t)u,

где A(t), B(t), H(t), C(t)-дифференцируемые необходимое число раз матричные функции времени. В данном случае

Таким образом, условия (8), (9) принимают вид

(14)

(15)

где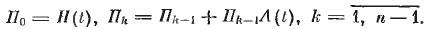

3. Управляемость

Понятие управляемости связано с переводом (переходом) системы посредством управления из одного состояния в другое. Этому понятию придается либо структурно-качественный, либо количественный смысл. При рассмотрении структурно-качественной стороны управляемости интересуются принципиальной возможностью перехода управляемой системы из одного заданного множества состояний в другое заданное множество состояний, как правило, за конечное время. При количественном изучении управляемости рассматривают те или иные характеристики переходных процессов при простейших типовых управляющих воздействиях. Управляемость обычно рассматривают применительно к детерминированным процессам, хотя возможно построение стохастических аналогов задач управляемости. Можно рассматривать управляемость как динамических объектов, не оснащенных регуляторами, так и систем, содержащих множество замкнутых контуров управления. В большой системе с иерархической структурой можно изучать управляемость каждого уровня (эшелона, страты), начиная от низшего и кончая высшим. В любом случае управляемость зависит от структуры системы, состава органов управления, значений параметров, располагаемой энергии управления

Может применяться и применяется целая группа понятий управляемости, различающихся как условиями перехода системы, так и ограничениями, накладываемыми на управление.

Классификация видов управляемости по этим признакам приведена в табл.1.

Таблица 1

Виды управляемости

Вид перехода	Ограничение на упрапление и номер парианта
содержательная формулировка	номер варианта	не ограничено	ограничено	Принимает дискретные значения	импульсный характер
Из произвольной точки пространства состояний R^nв произвольную точку R^n	I	I.1	I.2	I.3	I.4
Из произвольной точки замкнутой области размерности и пространства R^n в произвольную точку этой области	II	II.1	II.2	II.3	II.4
Из произвольной точки области размерности n пространства R^n в произвольную точку области меньшей размерности этого пространства	III	III.1	III.2	III.3	III.4
Из заданной области размерности m< n пространства R^n в заданную область размерности n	IV	IV.1	IV.2	IV.3	IV.4
Из произвольной точки х° пространства состояний R^n и любую точку малой окрестности х - х < е этой точки	V	V.1	V.2	V.3	V.4
Из произвольной точки заданной области подпространства R^m (m < n) в произвольную точку другой заданной области этого подпространства	VI	VI.1	VI.2	VI.3	VI.4
Из заданной точки пространства состояний R^n в другую заданную точку по заданной программной траектории	VII	VII.1	VII.2	VII.3	VII.4

Указанные здесь виды переходов иллюстрирует рис. 2.3.1. В случае I рассматривается переход из произвольной точки n-мерного пространства состояний в произвольную точку этого пространства, причем никаких ограничений на характер движения, кроме конечности времени перехода t1 - t0, не накладывается. В случае II в пространстве состояний задала замкнутая область G и должен обеспечиваться переход из любой точки этой области в произвольную се точку без выхода за пределы области G. Это случай существования ограничений типа неравенств в пространстве состояний.

Случай III соответствует переходу из заданной области пространства состояний полной размерности n в заданную область меньшей размерности. Например, управление должно обеспечивать переход из любой точки пространства состояний на прямую, проходящую через начало координат.

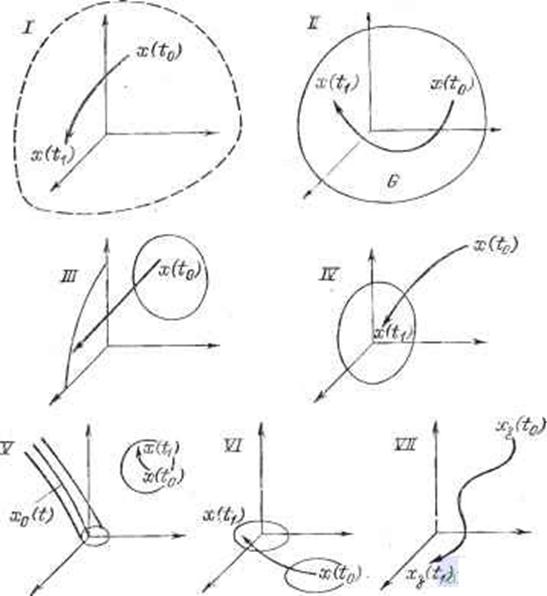
Рис. 2.3.1. Типы переходов при различных видах управляемости

Случай IV является как бы противоположным предыдущему: здесь управление должно обеспечить перевод системы из любой точки области меньшей размерности в любую точку полноразмерной области.

Случай V соответствует управляемости в малом. Здесь управление должно обеспечить переход из любой точки пространства состояний х° в любую точку малой n-мерной окрестности е точки х°. Порядок малости окрестности может быть связан со временем перехода.

Управляемости в малом может быть дано другое определение. Пусть при управлении u°(t) и начальном условии х°0 = х (t₀) имеет место процесс x°(t). При управлении u = u°(t) +∆u(t) процесс описывается функцией х°(t) + ∆x(t). Пусть каждая точка траектории х°(t) служит центром сферы радиусом е, где е - бесконечно малая величина: Огибающая указанных сфер образует е-трубку траекторий. Если можно указать управление ∆u(t), обеспечивающее прохождение траектории x°(t) + ∆x(t) через любую точку е-трубки, то система обладает управляемостью в малом.

Случай VI соответствует переходу из заданной области подпространства меньшей размерности m < n в заданную область того же подпространства. По отношению к определении I это может быть случаем неполной управляемости.

Важней практическое значение имеет понятие управляемости, соответствующее случаю VII. Здесь задается множество программных траекторий x3(t) перехода из одной точки х3(t0) в другую x3(t1). Система считается управляемой, если существуют управления, обеспечивающие движение по заданным траекториям при условиях

x(t₀) = x₃(t₀), x(t₁) = x₃(t₁).

Все эти понятия управляемости могут рассматриваться при различных условиях, накладываемых на управление. Четыре варианта этих условий указаны в табл. 1. В случае 1 никаких ограничений па вектор управления u(t) не накладывается (u принадлежит открытой области пространства управлений R^r). В случае 2 управление ограничено, оно должно принадлежать замкнутой области пространства R^r. В случае 3 управление все время (за исключением счетного множества моментов времени) имеет продельное значение, т. е. находится на границе замкнутой области пространства R^r. В случае 4 управление не ограничено по величине, но носит импульсный характер (типа векторной δ-функций). Переход системы здесь осуществляется мгновенно.

Итак, существует большое число видов управляемости (табл.1 содержит 28 видов). Эти виды применительно к линейным стационарным, линейным нестационарным, нелинейным системам изучены в разной степени, и трудности па пути их исследования различны. Положение здесь примерно аналогично тому, которое имеет место для наблюдаемости и идентифицируемости. Самым сильным в теоретическом и практическом отношении инструментом исследования управляемости является необходимый и достаточный аналитический и структурный критерий управляемости того или иного вида. Подобные критерии получены пока лишь для основных видов управляемости линейных систем. Во многих случаях приходится довольствоваться лишь необходимыми или достаточными критериями управляемости, а в ряде случаев лишь условиями, способствующими управляемости, подобие тому как это имеет место при изучении наблюдаемости.

Наконец, во многих практических задачах аналитические и структурные подходы анализа управляемости оказываются неприемлемыми по причине чрезмерной громоздкости или неразработанности. В этих случаях приходится прибегать к численному эмпирическому изучению управляемости путем моделирования.

Список использованных источников

Красовский, А.А. - Справочник по теории автоматического управления,1987

http://www.aznku.ru

1 Общие понятия о дифференциальном уравнении n-ого порядка и свойства уравнения

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x,y(x),y '(x),y ''(x), …,y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме:

y⁽ⁿ⁾ = f(x,y,y ', y '', …, y^{(n − 1)}).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия.

Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x₀) = y₀, y '(x₀) = y₁, y ''(x₀) = y₂, …, y^{(n − 1)}(x₀) = y_{n − 1}.

Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y '(x), y ''(x), …, y⁽ⁿ⁾(x)) = 0, x>x₀,

удовлетворяющего условиям

y(x₀) = y₀, y '(x₀) = y₁, y ''(x₀) = y₂, …, y^{(n − 1)}(x₀) = y_{n − 1}.

Условия y(x₀) = y₀, y '(x₀) = y₁, y ''(x₀) = y₂, …, y^{(n − 1)}(x₀) = y_{n −1} называются начальными данными, начальными условиями или данными Коши.

Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x), …, y⁽ⁿ⁾(x)) = 0, называется частным решением.

Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x), …, y⁽ⁿ⁾(x)) = 0

называется функция

y = Ф(x, С₁, С₂, …, С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, …, С_n, и обладающая следующими свойствами:

1. Ф(x, С₁, С₂, …, С_n) является решением уравнения при любых допустимых значениях С₁, С₂, …, С_m;

2. для любых начальных данных y(x₀) = y₀, y '(x₀) = y₁, y ''(x₀) = y₂, …, y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂, …, С_n = A_n, такие что решение y = Ф(x, A₁, A₂, …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁, С₂,..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Для решения уравнений, которые не интегрируются в квадратурах, применяются приближенные или численные методы.

Задача теории обыкновенных дифференциальных уравнений — исследование общих свойств решений, развитие точных, асимптотических и численных методов интегрирования уравнений.

Пусть f(x) — непрерывная на (a, b) функция и y(x) — ее первообразная. Тогда y '(x) = f(x), т.е. для отыскания первообразной получено дифференциальное уравнение 1-го порядка.

Решения этого уравнения известны:

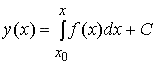
где С — произвольная постоянная, x ∈ (a, b), x₀ — некоторая точка из (a, b).

Чтобы выделить какое–то решение в задаче о вычислении первообразной, достаточно задать значение y(x) в какой–нибудь точке (a, b), например, y(x₀) = y₀.

Тогда решением задачи y '(x) = f(x), y(x₀) = y₀ является функция

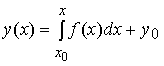
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции. Приведем некоторые примеры.

Пример 1.1.1. Найти функцию y(t) такую, что

y"'(t) + (y'(t))² - e^ly(t) = 1 +t, a < t < b.

Пример 1.1.2. Найти функцию u(t,x) такую, что

u_tt(t, x) + u_t(t, x) = (t² + x)u(t, x), a ^ t ^ b, c ^ x ^ d.

Пример 1.1.3. Найти функцию u(t,x) такую, что

u_t(t, x) — u_xx(t, x) + u(t, x) = 0, a ^ t ^ b, c ^ x ^ d.

Уравнение, содержащее производные неизвестной функции только по одной независимой переменной, называется обыкновенным диффе­ренциальным уравнением.

Уравнение, содержащее производные неизвестной функции по нес­кольким независимым переменным, называется дифференциальным уравнением в частных производных.

Уравнения, приведенные в примерах 1.1.1 и 1.1.2, являются обык­новенными дифференциальными уравнениями, уравнение из примера 1.1.3 - дифференциальным уравнением в частных производных.

Порядком дифференциального уравнения называется наибольший порядок входящих в него производных.

Данный курс посвящен, в основном, обыкновенным дифференциаль­ным уравнениям.

Обыкновенным дифференциальным уравнением первого порядка относительно неизвестной функции y(t) называется уравнение

F(t,y(t),y'(t))= 0, t е [a, b],

где F(t, y,p) - заданная функция трех переменных.

Обыкновенным дифференциальным уравнением n-го порядка отно­сительно неизвестной функции y(t) называется уравнение

F(t,y(t),y^t),...,y⁽ⁿ⁾(t)) = 0, t е [a,b],

где F(t, y,pi,..., p_n) - заданная функция n + 2 переменных.

2 Системы обыкновенных дифференциальных уравнений

Наряду с обыкновенными дифференциальными уравнениями можно рассматривать системы обыкновенных дифференциальных уравнений.

При решении уравнения (1.1) или системы (1.2) часто приходит­ся проводить операцию интегрирования. Процесс нахождения решений обычно называется интегрированием дифференциального уравнения или системы.

Нормальная система дифференциальных уравнений

В дифференциальные уравнения вида

может входить n неизвестных функций x1,…, xn. Тогда системой дифференциальных уравнений будет совокупность соотношений

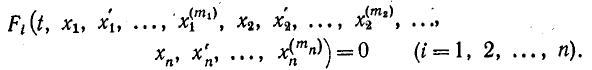
Предположим, что эту систему можно разрешить относительно старших производных. В этом случае получим систему уравнений:

Такая система называется канонической системой дифференциальных уравнений. Вводя новые неизвестные функции, можно привести эту систему к системе первого порядка. Пусть

Тогда наша система перепишется в виде

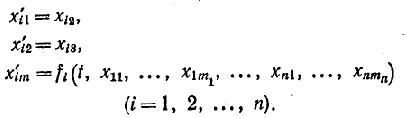
В дальнейшем будем рассматривать систему из n уравнений первого порядка в виде

Эта система называется нормальной (канонической) системой дифференциальных уравнений. Эту систему будем записывать в векторной форме:

Тогда данная система будет представлена в виде:

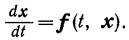
Решением этой системы на интервале G называется совокупность n функций x_i=x_i(t), определенных на интервале G и таких, что подстановка их в эту систему обращает каждое ее уравнение в тождество на всем интервале G.

Если вектор-функция не зависит явно от времени t, то эта система называется автономной (стационарной).

Задача Коши

Начальной задачей или задачей Коши для системы

называется следующая задача. Найти решение системы дифференциальных уравнений, определенное на некотором интервале G, содержащем точку t0, и удовлетворяющее условиям:

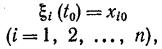
причем t₀, x_i0 (i=1, 2,…, n) называются начальными значениями для решения x₁(t), …, x_n(t), а эти условия – начальными условиями. Если ввести в рассмотрение (n+1)-мерное пространство с координатами t, x₁,…, x_n, то совокупность n функций x_i=x_i(t) будет представлять линию в n-мерном пространстве. Начальные значения t₀, x₁₀,…, x_n0 представляют собой точку в этом пространстве.

Свойства дифференциальных уравнений

Пусть имеется нормальная система дифференциальных уравнений в векторной форме

(1)

Общим решением системы (1) в области G называется совокупность n функций xi=xi(t,c1,…,cn), i=1,2,…,n. Будем говорить, что функция f(t,x1,…,xn) удовлетворяет условию Липшица в области G по переменным x1,…,xn, если существует такое постоянное число L>0, что для любой пары точек (t,x1,…,xn) и (t, xs1,…,xsn), принадлежащих G, выполняется неравенство

Пусть в системе (1) функции fi(t, x) непрерывны по t и удовлетворяют условию Липшица по x1,…,xn в некоторой области G. Тогда существует и притом единственное решение xi=xi(t), I=1,2,…n системы (1), удовлетворяющее начальным условиям xi(t0)=xi0, определенное на отрезке K, содержащем точку t0.

Теорема утверждает существование единственного решения на отрезке K, содержащем точку t0. Однако, это решение может быть продолжено за пределы отрезка K вплоть до границы области G.

Если функция f(t, x1,..., хn) имеет ограниченные частные производные по xi в выпуклой области G, то эта функция удовлетворяет условию Липшица

2.1 Автономной системой дифференциальных уравнений n –го порядка.

Рассмотрим автономную систему

Автономной системой дифференциальных уравнений n –го порядка называется система, которая в нормальной форме записывается в виде

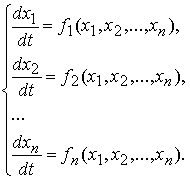
В векторной форме автономная система имеет вид x' = F(x) (не зависит от t), где

Название автономная система связано с тем, что поскольку производная x' зависит только от x и не зависит от t, то решение само управляет своим изменением. Автономные системы называют также динамическими системами.

Рассмотрим автономную систему

x' = F(x) с непрерывно дифференцируемой правой частью.

Уравнение x = φ(t) — t ∈ [a, b] — параметрическое уравнение фазовой траектории системы.

Пусть x = φ(t) — решение автономной системы, определенное на отрезке [a, b]. Множество точек x = φ(t), t ∈ [a, b] — кривая в пространстве R_xⁿ. Эту кривую называют фазовой траекторией или просто траекторией системы, а пространство R_xⁿ, в котором расположены фазовые траектории, называют фазовым пространством автономной системы.

Точка a называется положением равновесия (точкой покоя) автономной системы, если F(a) = 0.

Равенство x = φ(t), t ∈ [a, b] — параметрические уравнения фазовой траектории.

Интегральная кривая системы изображается в (n + 1) –мерном пространстве R_{x, t}ⁿ⁺¹ и может быть определена уравнениями

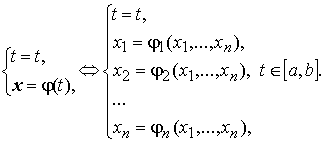
Ясно, что соответствующая фазовая траектория — проекция интегральной кривой на пространство R_x.

На рисунке приведено изображение интегральной кривой автономной системы и соответствующей фазовой траектории.

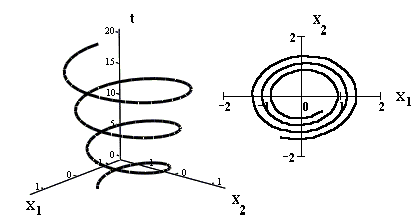
Построим интегральную кривую и фазовую траекторию решения задачи Коши

Задачу решим методом исключения:

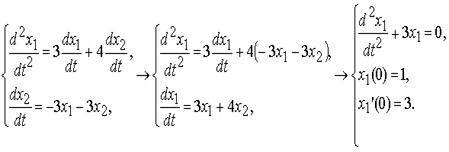
Решим задачи Коши для полученного линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами x₁'' + 3x₁ = 0:

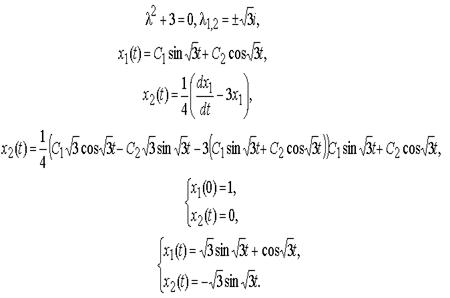
Имеем:

Соответствующая интегральная кривая определяется и пространстве R_x1,x2,t³ уравнениями

Фазовая кривая, которая является проекцией интегральной кривой на пространство R_x1,x2², определяется уравнениями

На рисунке приведены изображения интегральной кривой (слева) и соответствующей фазовой кривой (справа).

Важнейшим свойством решений автономных систем является следующее:

если вектор–функция x = φ(t) — решение автономной системы, то при любой постоянной C вектор–функция x = φ(t + C) тоже является решением системы.

3 Свойства фазовых траекторий

1. Две фазовые траектории либо не имеют общих точек, либо совпадают.

Это свойство фазовых траекторий означает, что фазовое пространство "расслаивается" на непересекающиеся фазовые траектории.

2. Если a — точка равновесия автономной системы, то x = a — фазовая траектория системы. Положение равновесия называют точкой покоя автономной системы.

3. Фазовая траектория, отличная от точки — гладкая кривая (в каждой точке этой кривой существует ненулевой касательный вектор).

4. Пусть x (t; x(0)) — решение задачи Коши x' = F(x), x(0) = x⁽⁰⁾. Тогда x(t₁ + t₂ ; x⁽⁰⁾) = x(t₂ ; x(t₁ ; x⁽⁰⁾) = x(t₁ ; x(t₂; x⁽⁰⁾) и x(− t; x(t; x⁽⁰⁾)) = x⁽⁰⁾.

Полную информацию о свойствах решений системы дают интегральные кривые..

Более того, некоторые свойства решений ярче проявляются при исследовании фазовых траекторий (фазового пространства системы).

Любую систему дифференциальных уравнений, записанную в нормальной форме, можно свести к автономной системе, увеличив число неизвестных функций на единицу:

Будем полагать, что для рассматриваемых автономных систем выполнены условия теоремы существования и единственности решения задачи Коши.

Таким образом, фазовые траектории системы – это проекции интегральных кривых в пространстве всех трех измерений x, y, t на плоскость x, y (рис.4.3).

Рисунок - фазовые траектории в пространстве

Если условия теоремы Коши выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая. То же справедливо, благодаря автономности, для фазовых траекторий: через каждую точку фазовой плоскости проходит единственная фазовая траектория.

Начислению в лицевых счетах плательщиков подлежат:

– налоговые обязательства, штрафные санкции и пеня, самостоятельно определенные плательщиком;

– налоговые обязательства, штрафные санкции и пеня, начисленные органом государственной налоговой службы и согласованные плательщиком в соответствии с действующим законодательством;

– пеня за нарушение установленных сроков погашения согласованного налогового обязательства;

– проценты за пользование рассрочкой (отсрочкой) налоговых обязательств;

– непогашенные суммы векселя, выдаваемого субъектом хозяйствования при осуществлении операций с давальческим сырьем во внешнеэкономических отношениях.

Порядок начисления в карточках лицевых счетов

Налоговые обязательства, штрафные санкции, пеня, самостоятельно определенные плательщиком в налоговой отчетности, вносятся в электронную базу данных подразделениями обработки и ведения налоговых документов и формируются в электронные и бумажные реестры. Специалисты подразделений администрирования учетных показателей и отчетности после переноса средствами программного
обеспечения данных из электронной базы отчетных документов в карточки
лицевых счетов налогоплательщиков формируют протокол ложных
записей по соответствующим кодам возможных ошибок. В зависимости от кода ошибки над их устранением работают сотрудники соответствующих подразделений.

После исправления ошибок производится повторное перенесение. Для проверки правильности выполнения указанных процедур подразделением администрирования учетных показателей и отчетности производится сверка сумм, разнесенных в карточки лицевых счетов, на соответствие суммам, занесенным в базы электронной отчетности. По результатам сверки на основании карточек лицевых счетов формируются реестры разнесенных сумм в двух экземплярах. Один экземпляр с отметкой инспектора указанного подразделения передается в отраслевое подразделение для хранения, второй экземпляр с отметкой отраслевого подразделения о получении хранится в подразделении администрирования учетных показателей и отчетности.
Итоговая проверка наличия не разнесенных сумм налоговых обязательств, срок уплаты по которым приходится на текущий месяц, осуществляется перед формированием сводных показателей информационной системы по состоянию на первое число следующего месяца. Проверка выполняется подразделением администрирования учетных показателей и отчетности с формированием протокола разногласий.

Начисление налоговых обязательств и штрафных с

Дата добавления: 2013-12-13