Знакопеременные ряды. Абсолютная и условная сходимость

1˚. Теорема (Признак Лейбница). Пусть 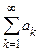знакопеременный ряд, то есть 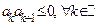, и пусть 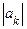убывает и стремится к нулю 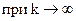.. В таком случае данный ряд сходится, при этом 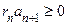и .

Доказательство. Пусть сначала 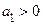. Тогда 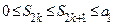, следовательно, . Если , 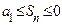. В любом случае, 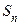заключено между нулём и 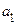. Потому сумма заключена между числами . Сходимость ряда следует из критерия Коши. Переходя к пределу 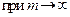, видим, что остаток 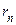заключен между числами . Ч и т.д.

Замечание. Из доказанной теоремы следует, в частности, сходимость “ряда Лейбница” , с которым мы встречались в §1.

2˚. Теорема. Если ряд 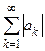сходится, то сходится и ряд 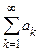. Обратное утверждение не верно.

Доказательство. Сходимость ряда 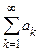сразу следует из критерия Коши для рядов ввиду неравенства 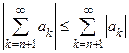. Контрпримером здесь может служить ряд Лейбница, который, как мы знаем, сходится, в то время как ряд из модулей его членов, т.е. гармонический ряд 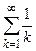, расходится.

Определение. Ряд 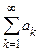называется абсолютно сходящимся, если сходится ряд из модулей его членов. Ряд называется условно сходящимся, если он сходится, но не абсолютно.

3˚. Приведём без доказательства два свойства абсолютно сходящихся рядов.

• В абсолютно сходящемся ряде можно производить любые перестановки его членов (т.е. перестановки не меняют сумму ряда).

· Два абсолютно сходящихся ряда можно почленно перемножить (как многочлен на многочлен). При этом суммы рядов также перемножатся.

Замечание. Легко доказать следующее утверждение (теорема Римана):

Если ряд условно сходится, то с помощью подходящей перестановки его членов сумму этого ряда можно сделать равной любому конечному числу или .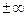

Дата добавления: 2013-12-13