Лекция 12. Пример решения кооперативной игры

Пример решения кооперативной игры

Лекция 11

неантагонистические игры n игроков (продолжение)

Пример 11.1 Кооперативная игра («джаз-оркестр»)

Игрок 1 («певец»), игрок 2 («пианист») и игрок 3 («ударник») могут получить от директора клуба 10 000 руб., если выступят вместе. Певец и пианист вдвоем могут получить 8 000 руб., ударник и пианист—6 500 руб., один пианист—3 000 руб., певец и ударник—5 000 руб., один певец—2 000 руб., а один ударник ничего не может заработать.

Таким образом, мы рассматриваем кооперативную игру, в которой N= {1,2,3}, u ({1,2,3})= u (1,2,3)=10 000, u (1,2)=8 000, u (2,3)=6 500, u (2)=3 000, u (1,3)=5 000, u (1)=2 000, u (3)=0.

Основная задача теории кооперативных игр—оптимальное распределение максимального суммарного выигрыша u (N) между игроками.

Пусть d_i —сумма, которую получает игрок i при распределении максимального суммарного выигрыша u (N).

Вектор d =[ d ₁, d ₂,…, d_n ] ^T, удовлетворяющий условиям индивидуальной и коллективной рациональности

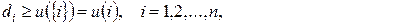(11.1.1)(11.1.2)

называется дележом.

Для того чтобы вектор d =[ d ₁, d ₂,…, d_n ] ^T был дележом в кооперативной игре необходимо и достаточно, чтобы

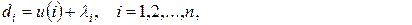(11.1.3)(11.1.4)(11.1.5)

Игра называется существенной, если

(11.1.6)

В противном случае игра называется несущественной. Несущественная игра имеет единственный дележ d =[ u (1), u (2),…, u (n)] ^T, а всякая существенная игра имеет бесконечное множество дележей.

Дележ d доминирует дележ g по коалиции S, если

(11.1.7)

(11.1.8)

Это значит, что дележ d лучшедележа g для всех игроков коалиции S и при этом реализуем коалицией S.

Дележ d доминируетдележ g, если существует такая коалиция S, по которой дележ d доминируетдележ g.

Множество недоминируемых дележей кооперативной игры называется ее C-ядром.

Недоминируемый дележ устойчив в том смысле, что ни одной из коалиций невыгодно отделиться от других игроков.

Для того чтобы дележ принадлежал C-ядру необходимо и достаточно выполнение для всех коалиций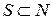

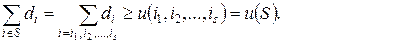(11.1.9)

В примере 11.1 («джаз-оркестр») дележ d =[ d ₁, d ₂, d ₃] ^T, принадлежит C-ядру, когда

Эта система описывает выпуклый многогранник, точнее многоугольник, а еще точнее треугольник с дележами-вершинами [3 500, 4 500, 2 000] ^T, [3 500, 5 000, 1 500] ^T, [3 000, 5 000, 2 000] ^T. Можно выбрать из всех дележей, принадлежащих C-ядру, то есть из всех точек треугольника, дележ (точку), составленный из среднеарифметических величин [3 333, 4 833, 1 833] ^T. В этом случае все коалиции из двух игроков имеют одинаковый дополнительный доход, равный d ₁+ d ₂ – u (1,2)=166, d ₁+ d ₃ – u (1,3)=166, d ₂+ d ₃ – u (2,3)=166. Такой дележ является справедливым компромиссом внутри C-ядра.

Дележи, принадлежащие C-ядру, не доминируются никакими другими дележами, но нельзя утверждать, что в C-ядре для любого заданного дележа найдется доминирующий его дележ.

Другим множественным принципом оптимальности в кооперативных играх, применение которого на практике, к сожалению, невозможно, является H–M- решение.

Подмножество дележей кооперативной игры называется H–M- решением, если:

1) из того, что дележ d доминируетдележ g, следует, что, либо дележ d не принадлежит данному подмножеству, либо дележ g не принадлежит данному подмножеству (внутренняя устойчивость);

2) для любого дележа g, который не принадлежит данному подмножеству, существует такой дележ d, который тоже не принадлежит данному подмножеству и доминируетдележ g (внешняя устойчивость).

Если C-ядро не пусто и H–M- решение существует, то оно содержит C-ядро. Действительно, пусть дележ g принадлежит C-ядру. Если он не принадлежит H–M- решению, то найдется дележ d, который доминируетдележ g, что противоречит принадлежности этого дележа к C-ядру как множеству недоминируемых дележей.

Необходимо отметить, что C-ядро и H–M- решение могут включать в себя много разных дележей. С другой стороны H–M- решение не всегда существует, а C-ядро может оказаться пустым. Поэтому представляют интерес принципы оптимальности, существование и единственность которых были бы обеспечены в любой кооперативной игре.

вектор шепли

Дата добавления: 2013-12-13